统计R语言代写 R语言代写统计代写

STA130H1F

Week 5 Problem Set

统计R语言代写 There are two parts to your problem set. One is largely R-based with short written answers and the other is more focused on writing.

Instructions

How do I hand in these problems for the 11:59 a.m. ET, October 16 deadline?

Your complete .Rmd fifile that you create for this problem set AND the resulting .pdf (i.e., the one you ‘Knit to PDF’ from your .Rmd fifile). Late problem sets or problems submitted another way (e.g., by email) are not accepted.

Problem set grading 统计R语言代写

There are two parts to your problem set. One is largely R-based with short written answers and the other is more focused on writing. We recommend you use a word processing software like Microsoft Word to check for grammar errors in your written work. Note: there can be issues copying from Word to R Markdown so it may be easier to write in this fifile fifirst and then copy the text to Word. Then you can make any changes flflagged in Word directly in this fifile.

Part 1 [Question 1]

A criminal court considers two opposing claims about a defendant: they are either innocent or guilty. In the Canadian legal system, the role of the prosecutor is to present convincing evidence that the defendant is not innocent. Lawyers for the defendant attempt to argue that the evidence is not convincing enough to rule out that the defendant could be innocent. If there is not enough evidence to convict the defendant and they are set free, the judge generally does not deliver a verdict of “innocent”, but rather of “not guilty”.

(a) If we look at the criminal trial example in the hypothesis test framework, which would be the null hypothesis and which the alternative?

(b) What does a type 1 error mean in this context?

(c) What does a type 2 error mean in this context?

[Question 2] 统计R语言代写

(Adapted from “Biostatistics for the Biological and Health Sciences”)

Many students have had the unpleasant experience of panicking on a test because they found the fifirst question very diffiffifficult. A study was conducted to study the relationship between the ordering of test questions and student anxiety. The following scores are measures of “test anxiety” (i.e. panic or blanking out), based on data from “Item Arrangement, Cognitive Entry Characteristics, Sex, and Test Anxiety as Predictors of Achievement in Examination Performance”, by Klimko (2015). Note that higher scores indicate higher anxiety.

test_ordering <- c(rep("easy_to_hard", 25), rep("hard_to_easy", 16));
anxiety_score <- c(24.64, 39.29, 16.32, 32.83, 28.02,
                    33.31, 20.60, 21.13, 26.69, 28.90,
                    26.43, 24.23, 7.10,  32.86, 21.06,
                    28.89, 28.71, 31.73, 30.02, 21.96,
                    25.49, 38.81, 27.85, 30.29, 30.72,
                    33.62, 34.02, 26.63, 30.26,
                    35.91, 26.68, 29.49, 35.32,
                    27.24, 32.34, 29.34, 33.53,
                    27.62, 42.91, 30.20, 32.54)
# cbind 'sticks' two vectors together, each in its own column 
anxiety_data <- tibble(test_ordering, anxiety_score)
glimpse(anxiety_data)

## Rows: 41
## Columns: 2
## $ test_ordering <chr> “easy_to_hard”, “easy_to_hard”, “easy_to_hard”, “easy…
## $ anxiety_score <dbl> 24.64, 39.29, 16.32, 32.83, 28.02, 33.31, 20.60, 21.1…

(a) Construct boxplots of anxiety_score for each type of test. Write 2-3 sentences comparing the distributions of anxiety scores for the two types of test.

(b) Do these data support the claim that the median anxiety level is difffferent for tests with questions ordered from easiest to hardest and tests with questions ordered from hardest to easiest?

(i)State the hypotheses you are testing (be sure to defifine any parameters you refer to).

(ii)Look at the code below and write a few sentences explaining what the code inside the for loop is doing and why.

test_stat <- anxiety_data %>% group_by(test_ordering) %>% 
  summarise(medians = median(anxiety_score)) %>% 
  summarise(value = diff(medians))
test_stat <- as.numeric(test_stat)
test_stat

## [1] 3.28

set.seed(523)
repetitions <- 1000;
simulated_values <- rep(NA, repetitions)

for(i in 1:repetitions){
  simdata <- anxiety_data %>% mutate(test_ordering =       sample(test_ordering))

  sim_value <- simdata %>% group_by(test_ordering) %>% 

    summarise(medians = median(anxiety_score)) %>% 
    summarise(value = diff(medians))

  simulated_values[i] <- as.numeric(sim_value)
}

sim <- tibble(median_diff = simulated_values)

sim %>% ggplot(aes(x=median_diff))+ geom_histogram(binwidth=1,color="black",fill="gray")

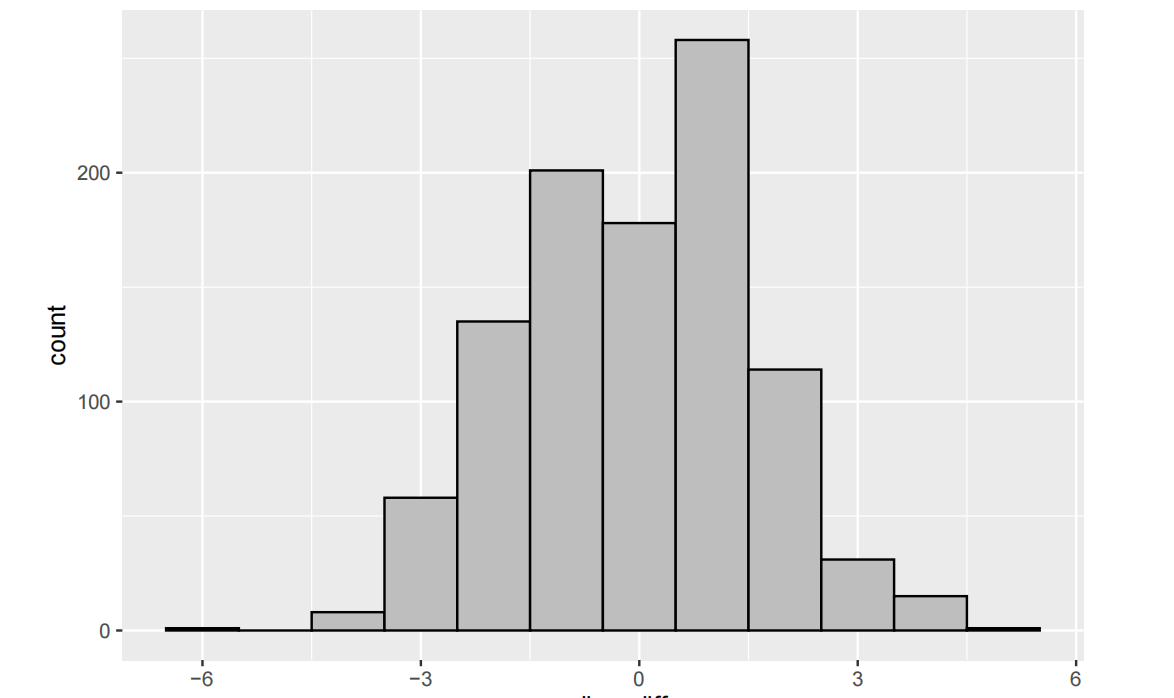
# Calculate p-value 
num_more_extreme <- sim %>% filter(abs(median_diff) >= abs(test_stat)) %>% summarise(n())

p_value <- as.numeric(num_more_extreme / repetitions)
p_value

## [1] 0.037

(iii) Write a few sentences summarizing your conclusions. Be sure to interpret the p-value carefully and to clearly address the research question.

[Question 3]

(Adapted from “Biostatistics for the Biological and Health Sciences”) The table below presents data from a random sample of passengers sitting in the front seat of cars involved in car crashes. Researchers are interested in whether the fatality rates (i.e. death rates) diffffer for passengers in cars with airbags and passengers in cars without airbags.

The code below creates a tidy data frame for this problem, using the R command rep. This function creates a vector which replicates its fifirst argument the number of times indicated by its second argument. For example, the rep(“hello”, 5) creates a vector with 5 elements, each of which is “hello”. Run the code chunk below to load a tidy tibble called data which you’ll use for the remainder of this question.

library(tidyverse)

data <- tibble(group=c(rep("airbag",11541),rep("no_airbag",9853)),
                    outcome=c(rep("dead",41),rep("alive",11541-41),
                              rep("dead",52),rep("alive",9853-52)))

(a) State appropriate hypotheses to compare the proportions of deaths in cars with and without airbags. Be sure to defifine any parameters you refer to in your hypotheses.

(b) Carry out a hypothesis test for the hypotheses stated in part (a).

set.seed(523) # Replace the number in the parentheses with the 1st, 3rd, and 5th # digits in your student number.

(c) Based on your answer in part (b), would you reject the null hypothesis at the 0.05 signififi- cance level?

(d) Based on your answer in part (c), what kind of error did you possibly make?

[Question 4] 统计R语言代写

In class we’ve talked about two kinds of hypothesis tests. In the fifirst kind (week 4) we talked about how to test whether a proportion is equal to a specifific value, with hypotheses of the form: H₀ : p = p₀ vs H_A : p = p₀. In this week’s class (week 5), we talked about how to test if there is a difffference between two groups (e.g. a difffference in the means of two groups, the medians of two groups, or proportions of two groups). A test for the difffference between the means of two groups takes the form: H₀ : µ₁ = µ₂ vs H_A : µ₁ = µ₂.

For each of the following scenarios, state appropriate hypotheses H₀ and H_A. Be sure to carefully defifine any parameters you refer to.

(a) A university professor wants to learn about factors which affffect student learning. She records which students attend all 10 weekly tutorials and which students miss one or more tutorials, and is interested in determining if there is an association between this and scores on the fifinal exam. 统计R语言代写

(b) A health survey asked individuals to report the number of times they exercised each week. Researchers were interested in determining if the proportion of individuals who exercised at least 3 times per week diffffered between people who drink coffffee every day and people who do not drink coffffee every day.

(c) A study was conducted to examine whether the sex of a baby is related to whether or not the baby’s mother smoked while she was pregnant.

(d) Based on results from a survey of graduates from the University of Toronto, we would like to compare the median salaries of graduates of statistics programs and graduates of computer science programs.

Part 2 统计R语言代写

Write a short summary of ONE of the following studies. A written summary must include the following components:

1.Context of the problem (i.e. introduction) 2. Summary of the methods. E.g. State hypotheses; defifine the test statistic; etc. 3. Summary of the fifindings (i.e. the main results) 4. Conclusion (e.g. main fifinding(s), signifificance, etc.). 5.Limitations (optional for now, but good practice and required for the fifinal project; e.g. study design issues etc.)

(a)

A health survey asked 200 individuals aged 20-45 living in Toronto to report the number minutes they exercised last week. Researchers were interested in determining whether the average duration of exercise diffffered between people who consume alcohol and those who do not consume alcohol. Assume the researchers who conducted this study found that people who drank alcohol exercised, on average, 20 minutes per week. In contrast, people who did not drink alcohol exercised 40 minutes per week, on average. The researchers reported a p-value of 0.249.

(b)

A study was conducted to examine whether the sex of a baby is related to whether the baby’s mother smoked while she was pregnant. The researchers obtained a sample of 10,000 births from a birth registry of all children born in Ontario in 2018. The researchers found that based on this sample 4% of mothers reported smoking during pregnancy and 52% of babies born to mothers who smoked were male. In contrast, 51% of babies born to mothers who did not smoke were male. The researchers reported a p-value of 0.50.

(c) 统计R语言代写

Based on results from a survey of graduates from the University of Toronto, we would like to compare the median salaries of graduates of statistics programs and graduates of computer science programs. 1,000 recent graduates who completed their bachelor’s degree in the last fifive years were included in the study; 80% of the respondents were female and 20% were male. Among statistics graduates, the median reported income was $76,000. Among computer science graduates, the median reported income was $84,000. The researchers reported a p-value of 0.014.

(d)

A team of researchers were interested in understanding millennials’ views regarding housing affffordability in Toronto. The team interviewed 850 millennials currently living in Toronto. 84% reported that they felt housing prices were unaffffordable in the city. Suppose the researchers were interested in testing whether this proportion was difffferent from a study published last year, which found that 92% of millennials reported that housing costs were unaffffordable. The researchers reported a p-value of 0.023.

(e)

Suppose a drug company was interested in testing a new weight-loss drug. They enrolled 20,000 participants and assigned 10,000 to take their new drug, SlimX, and 10,000 to take a placebo. The researchers found that over 2 months, participants who took SlimX lost, on average, 5 lbs. In comparison, the control group lost 4.5 lbs during the same time. The researchers reported a p-value of <0.0001.

Some things to keep in mind

Try to not spend more than 20 minutes on the prompt.
Aim for more than 200 but less than 500 words.
Use full sentences.
Grammar is not the main focus of the assessment, but it is important that you communicate in a clear and professional manner (i.e., no slang or emojis should appear).
Be specifific. A good principle when responding to a writing prompt in STA130 is to assume that your audience is not aware of the subject matter (or in this case has not read the prompt).
You cannot directly copy the sentences from the explanation provided. You also cannot use quotation marks in your response. You must rewrite these responses in your own words (i.e. paraphrase).

Vocabulary

Type I and II error
Comparing two population means/proportions
One- and two-sample hypothesis test

其他代写： code代写 CS代写 cs作业代写 Data Analysis代写 essay代写英国代写 Exercise代写 finance代写 homework代写北美作业代写 algorithm代写 analysis代写 app代写 assembly代写 C/C++代写

合作平台：essay代写论文代写写手招聘英国留学生代写