Problem Set 5
Statistics 506
统计506代写 In this question you will use R’s data.table package to answer a question of your choosing about the RECS data used in previous problem sets.
Question 1 [40 points] 统计506代写
In this question you will use R’s data.table package to answer a question of your choosing about the RECS data used in previous problem sets.
a. [5 points] Pose a question about US residential homes that can be answered using one or both of the 2009 and 2015 RECS data sets. Then identify the variables that will be used answer the question. This question should not simply repeat posed in this (or any previous years) problem sets or examples.
b. [30 points] Carry out an analysis that helps you to answer the question you pose in part a using the data.table package for computations. As always, provide confifidence intervals for all point estimates and present your results in nicely formatted graphs and/or tables.
c. [5 points] Answer the question you posed in part a using evidence from your analysis in part b. Your answer should be ~2-5 sentences.
Note 统计506代写
The question you pose in part a should be about homes in the US, not about the data itself. See the good and bad examples below for an illustration of the distinction.
A good question for part a:
For which states (or reportable domains) has home internet access most chagned between 2009 and 2015? Is this difference larger in urban or rural areas?
A bad question for part a:
For each state, how many homes in the 2009 and 2015 RECS samples didn’t have internet access? Report by urban / rural. The key difference is that the “good” version asks an inferential questions while the “bad” version focuses on the data itself, rather than the population it represents.
Question 2 [45 points] 统计506代写
In this question, you will use cross-validation to compare the out-of-sample performance of three approaches to building models of the relationship between age and the presence of a permanent tooth. These approaches will build on what you did for question 2 in problem set 4. In the process, you will make use of asynchronous and/or parallel computing to speed up the model building and evaluation process. You can treat the data as iid for this question and do not need to make use of the survey weights or design.
a. [8 points] For subjects with a complete dentition exam in the NHANES data from problem set 4, create a data.table in long format where each row is the “Tooth Count” (e.g. OHX[0-9]{2}TC ) status for a subject. Create a flflag for whether a permanent tooth is present and merge in the subject’s age from the demographics data. Here is a screen-shot for reference:
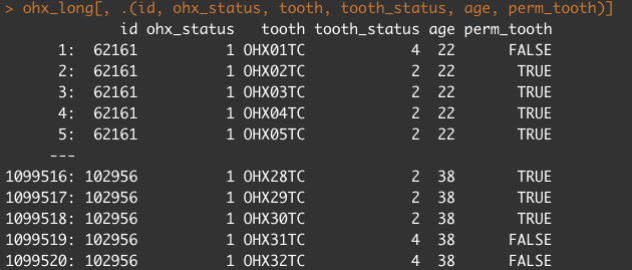
b. [2 points] Create a variable dividing the data into 4 folds based on the cohort from which the subjects came.
c. [30 points] For each modeling approach described below, use the function mgcv::bam( ) (“big additive model”) to fifit the model described to the training folds. Then, use the predict( ) method to estimate the probability that the a permanent tooth is present for each tooth in the held out fold. Repeat to get cross-validated predictions for each tooth. Use some form of parallel or asynchronous computing for this part.
d. [5 points] Compare the approaches below in terms of the cross-validated cross entropy loss (https://en.wikipedia.org/wiki/Cross_entropy). Here, is any of the cross-validated predictions from part “c” and when a permanent tooth is present:
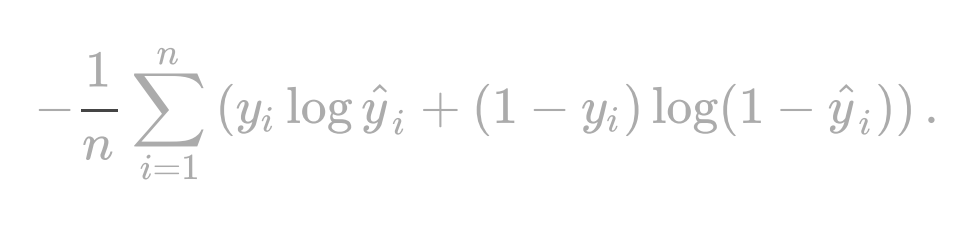
Approaches: 统计506代写
1.Use logistic regression to model the probability that a tooth is present as a smooth function of age (using a cubic smoothing spline) common to all teeth and a per-tooth indicator variable. Account for dependence among teeth within an individual subject using a random intercept. Using the variable names from the screen shot in part “a” the formula is:
perm_tooth ~ tooth + s(age, bs = ‘cs’) + s(id, bs = ‘re’) .
2.Repeat the previous approach, but include an interaction between tooth and age as follows:
perm_tooth ~ tooth + s(age, bs = ‘cs’, by = ‘tooth’) + s(id, bs = ‘re’) .
3.Repeat the previous step by modeling each tooth separately, so that the random intercepts are no longer needed:
perm_tooth ~ s(age, bs = ‘cs’) .
Notes:
The data for question 2 are available in the Stats506_F20 repository under problem_sets/data/ . You will need the following two fifiles:
- nahanes_demo.csv
- nhanes_ohxden.csv

其他代写:homework代写 java代写 matlab代写 program代写 project代写 essay作业代写 finance代写 python代写 essay代写 report代写 paper代写 assignment代写 加拿大代写 作业代写 作业加急 北美代写 英国代写 北美作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
