STA130H1F
Week 9 Problem Set
统计问题集代做 Instructions How do I hand in these problems for the 11:59 a.m. ET, November 20th dead-line? Your complete .Rmd file that you create for this
Instructions 统计问题集代做
How do I hand in these problems for the 11:59 a.m. ET, November 20th dead-line?
Your complete .Rmd file that you create for this problem set AND the resulting .pdf (i.e., the one you ‘Knit to PDF’ from your .Rmd file) must be uploaded into a Quercus assignment (link:https://q.utoronto.ca/courses/184002/assignments/465522) by 11:59 a.m. ET, on November 20th. Late problem sets or problems submitted another way (e.g., by email) are not accepted.
Problem set grading
There are two parts to your problem set. One is largely R-based with short written answers and the other is more focused on writing. We recommend you use a word processing software like Microsoft Word to check for grammar errors in your written work. Note: there can be issues copying from Word to R Markdown so it may be easier to write in this file first and then copy the text to Word. Then you can make any changes flagged in Word directly in this file.
Part 1 统计问题集代做
Question 1
In this question, you’ll be working with housing price data for a sample of house sales which occurred in Ames, Iowa between 2006 and 2010. These data come from Kaggle, an open data science competition.
(a)
Create a new variable called Square_feet which indicates the total living space (in square feet) of the first and second floors of each house (i.e. sum of FirstFlrSF, SecondFlrSF, and TotalBsmtSF)
(b)
Create a visualization showing the association between the total living space (in square feet) and the sale price (SalePrice). Describe the association in 1-3 sentences.
(c)
Fit a linear regression model to predict Sale price using only house size (Square_Feet) as a predictor. Write the regression equation, state the null and alternative hypotheses to assess whether there is a linear association between the two variables, and make a conclusion based on your fitted model.
(d) 统计问题集代做
Add a new categorical variable called Fireplace2 to the house_sales dataset, which indicates whether each house has a fireplace (YES) or not (NO). Create a visualization to compare the distribution of sale price for houses with and without fireplaces, and write 2-3 sentences comparing these distributions. Hint: look at the Fireplaces variable in the original house_sales dataset.
(e)
Fit a linear regression model to predict sale price (SalePrice) using only Fireplace2 as a predictor. Write the regression equation (make sure you clearly identify the baseline level), state the null and alternative hypotheses to assess whether there is a linear association between the two variables, and make a conclusion based on your fitted model.
(f) 统计问题集代做
Divide the dataset into training (80%) and testing (20%) datasets. Build four regression models based on the training data: (i) only Square_feet as a predictor; (ii) only Fireplace2 as a predictor; (iii) both predictors, but no interaction (parallel lines); (iv) both predictors and their interaction. Set the seed to be the last three digits of your student ID number.
(g)
Use each of the four models from (f), to make predictions for both the testing data and the training data, and calculate the RMSEs in each case. Which of the models do you think is most suitable for prediction?
(h)
What is the predicted price of a 1200 square foot home with a fireplace, based on each of the four models you built in (f)?
Question 2 统计问题集代做
(Adapted from Practical Business Statistics)
Suppose you are interested in finding the temperature that maximizes the yield for an industrial process.
These data are given in the dataframe yield
yield <- tibble(temperature = seq(from=600, to=850, by=25), yield = c(127, 139, 147, 147, 155, 154, 153, 148, 146, 136, 129))
(a) Plot the data and superimpose the best (straight line) linear predictor for yield, based only on the temperature. Does this line capture the relationship between temperature and yield?
yield %>% ggplot(aes(x=temperature, y=yield)) + geom_point() + geom_smooth(method="lm", se=FALSE)
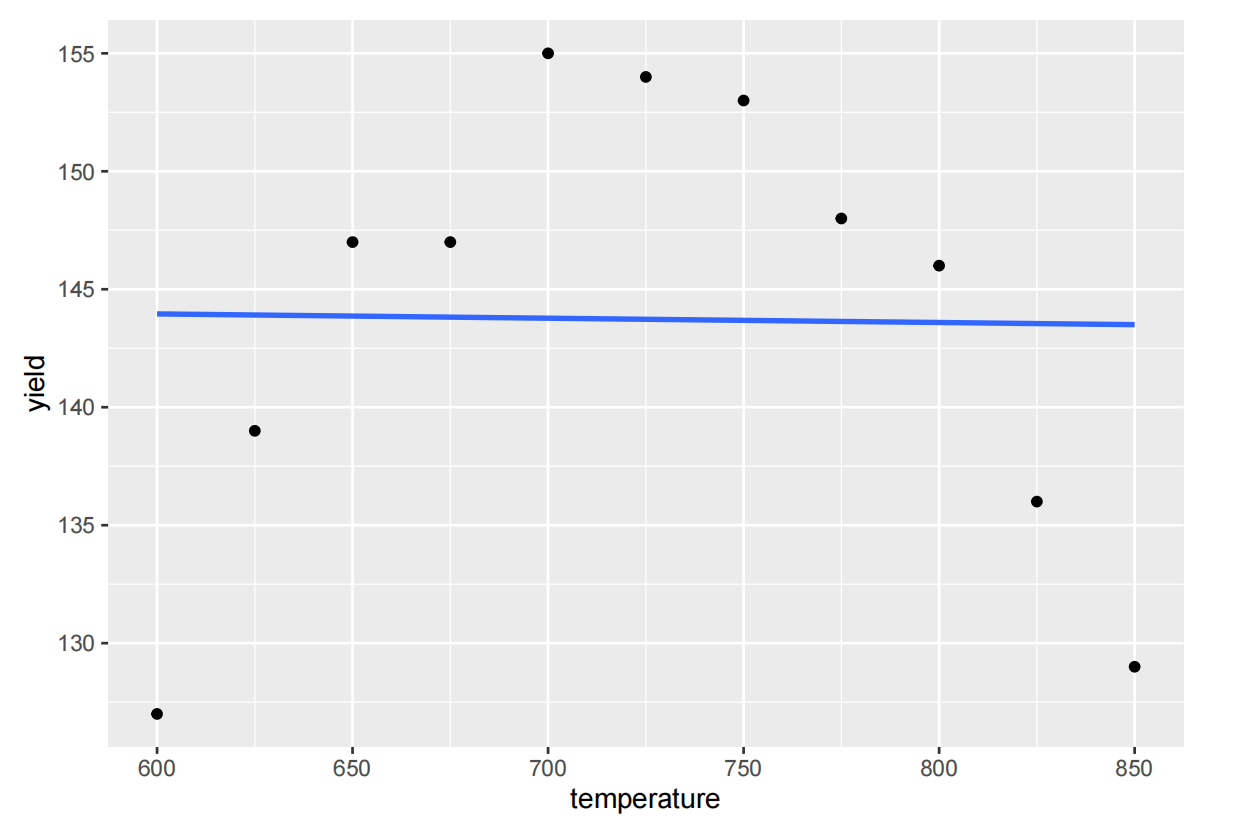
The simple linear regression model with only temperature as a predictor for yield does not capture the association between temperature and yield. The association between temperature and yield is clearly quadratic rather than linear.
(b) Add a new variable temperature_squared which is the square of temperature to the existing data frame. Then write down the following regression models:
(i) Model 1: with only ‘temperature‘ as a predictor and yield
(ii) Model 2: with both ‘temperature‘ and ‘temperature_squared‘ as predictors.
Be sure to defifine any notation you introduce.
(c) Is Model 2 still a linear model, even though it includes a squared term? Justify your answer.
(d) Using R, fit the two regression models you defined in (c). Which model do you think would best explain the association between temperature and yield? Justify your answer in 1-2 sentences.
(e) What could you calculate to determine which fitted model better explains the variability in yield? Calculate this value for both models and comment on your findings.
Part 2 统计问题集代做
Prior to starting the activity, you must review the video on plagiarism which can be found at Modules à Course information and other useful things à Writing Skills Videos à Plagiarism video. This video goes over the 6 most common types of plagiarism and how to avoid them.
Once you have watched the video, please see Quercus for the following article: Kramer A, Guillory J, Hancock J. “Experimental evidence of massive-scale emotional contagion through social networks”. PNAS 2014; 111 (24): 8788-90.
Prepare a brief, half-page summary of the above study. Make sure you explain the following, at a minimum:
– Objective: What were the authors interested in studying?
– Methods: What type of study design was used? Who were the participants? What statistical tests were used?
– Results: What were the main findings of the study? Make sure you support any statements with facts (e.g. proportions, p-values, etc.).
- Conclusions: What were the main take away messages? Were there any important limitations to the study?
You can provide your summary in abstract form (i.e., using the headers above), but make sure you use complete sentences. Because you are being asked to paraphrase the entire piece, you do not need to include an in-text citation.