统计网课托管 STA255代写

STA255 Week-9 (Day-1)

Shahriar Shams 09/03/2020

统计网课托管 Idea of PivotalQuantityConfidence interval(CI) for µwith-population variance (σ2) known (using Z)-population variance (σ2) unknown (using t)

Review of Week-8 统计网课托管

Idea of intervalestimation
Definition of confidenceinterval

– 100*(1 − α)% CI for µ =⇒ P [l(X₁, …X_n) ≤ µ ≤ u(X₁, …X_n)] = 1 − α

Idea of PivotalQuantity
Confidence interval(CI) for µwith

-population variance (σ²) known (using Z) 统计网课托管

-population variance (σ²) unknown (using t)

Two sided vs one sidedCI
Interpretation of confidenceinterval

-Interpretation does not involve the two numeric numbers that we calculate.

Learning goals

Confidence interval for populationproportion
Sample sizecalculation

Confidence interval for population proportion 统计网课托管

Last week we constructed confidence interval for population mean(µ).
Weused either
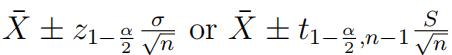
统计网课托管
Oneway to look at this:2 n 2 n

-weuse sample mean (X¯ ) as a point estimator

-WEcalculated the standard error of the estimator,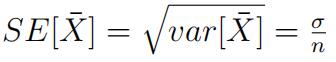

-We wrote 100*(1 − α)% CI as

point estimator ± z₁₋ α standard error

Supposep is the proportion of “success” in a population.
- “success” represent one of the outcomes of a Bernoulli trial. 统计网课托管
The goal is to construct a confidence interval for p.
Supposewe take a sample of n observation and find X number of success out of n.
Thenpˆ = X is a natural estimate/estimator of p.
SinceX is the number of success in n trials with probability of success being p in each trial,

X ∼ Bin(n, p)

We know,E[X] = np and V [X] = np(1 − p)
Therefore,
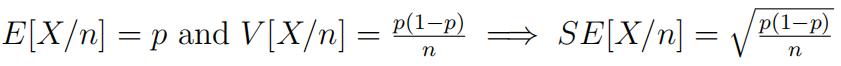
统计网课托管
Since, p is unknown, it’s not possible to calculate the standard error of X/n
Oneway to estimate the standard error is to replace p by the sample proportion (pˆ)
Thisgives us estimated standard error =
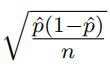
We can write,

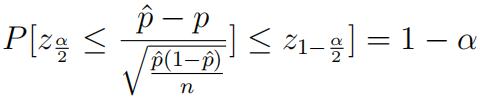
Re-arranging the above expression we get the 100*(1 − α)% CI for p as

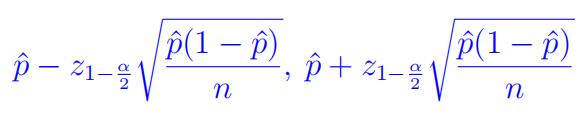
Sample Size calculation 统计网课托管

Width of an interval

Letl and u be the lower and upper value of an interval.
Width of an interval = u −l
ForCI for µ with σ known,

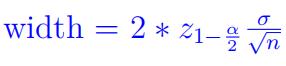
Margin of error

Keepingthe point estimator in the middle adding or subtracting a quantity gives us confidence intervals.
Thequantity that we add or subtract is called the margin of error.
ForCI for µ with σ known, margin of error =

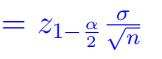
Sample size as a function of width or margin or error 统计网课托管

We can see, width = 2* margin oferror
Ifmargin of error increases, width will also increase.
Ifwe look at the expression of the margin of error(ME) we will see

– σ ↑ =⇒ M E ↑

– (1 − α) ↑ =⇒ M E ↑

– n ↑ =⇒ M E ↓

Atypical sample size calculation involves an statement like, “If we want the 95% CI for µ to have a width no longer 10, how many samples should we collect given that the population standard deviation is known to be 25”. 统计网课托管

From this statement, σ = 25, z₀_.₉₇₅= 1.96 and width < 10
We get aninequality,

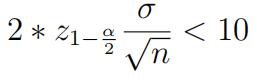
Re-arranging this we get,

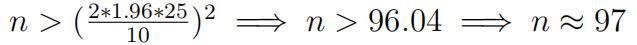
Sample size calculation for population proportion 统计网课托管

Samplesize calculation involves plugging in a value of the population standard deviation.
Whenit’s unknown, we put a reasonably large value of sigma which is also known as “conservative” approach as this gives us the widest interval.
Aswe have seen on page-2 of this document, CI for proportion involves the unknown parameter p in the standard error expression.
Standarderror involves p(1 − p). Since p is bounded between 0 and 1, it is possible to get a sense of the maximum value of p(1 − p).
It can be shown that the maximum valueof p(1 p) = 1/4 which is resulted when p = 1/2 统计网课托管

This will give us the widest interval.
Atypical sample size calculation for proportion involves a statement like, “If we want the 95% CI for the true proportion to have a width no longer than 0.1, how many samples we should collect?
For this we get theinequality,

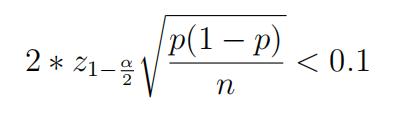
Replacing p(1 − p) by 1/4 we get,

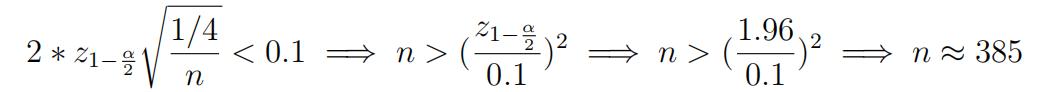
Chapter 8.4 and 8.5 not needed.

Homework

Chapter 8.1

4(e), 5(c,d), 7

Chapter 8.2

20, 21, 23, 25

Chapter 8.3

33, 38

合作平台：essay代写论文代写写手招聘英国留学生代写