Practice Problems Stats 426
统计练习题代写 Here are some problems to try in addition to homework, quiz, and midterm problems. 1) Let Y1, Y2, . . . Ynbe iid from the density function
Here are some problems to try in addition to homework, quiz, and midterm problems.
1)
Let Y1, Y2, . . . Ynbe iid from the density function

Without any calculations, use what you know about the chi-square and F distributions to find the distribution of X1/X2.
3) 统计练习题代写
Recall the Hardy-Weinberg problem described in your text (page 273-274). The multinomial distribution for random variables Y1, Y2, Y3 (can extend to more than 3) is given by

where y1 + y2 + y3 = n and the parameters p1, p2, p3 are subject to the constraint p1 + p2 + p3 = 1. This distribution is an extension of the binomial distribution. In fact, the distribution of each Yi, i = 1, 2, 3 is binomial. So, for example, E[Y1] = np1 and V ar(Y1) = np1(1−p1). If gene frequencies are in equilibrium, the genotypes AA, Aa, and aa occur in a population with proportions
p1 = (1 − θ)2 , p2 = 2θ(1 − θ) , and p3 = θ2
according to Hardy-Weinberg law.
a) Using the multinomial as the likelihood and a prior distribution of θ ∼ Beta(10, 10), find the Bayes estimator of θ. That is find E[θ|y].
b) Is the Bayes estimator unbiased?
4) 统计练习题代写
Consider the following probability model:
Likelihood : Y1, . . . , Yn independent and identically distributed Poisson(θ) Prior : θ ∼ Gamma(α, λ) , α , λ fixed
a) Find the posterior distribution p(θ | y).
b) Find E[θ | y] and V ar(θ | y).
c) Find the marginal distribution p(y). Note that this is the joint discrete distribution
P(Y1 = y1, Y2 = y2, . . . , Yn = yn). (This distribution will be conditional on α and λ).
For any Yi , i = 1, . . . , n, find E[Yi ] and V ar(Yi).

6) 统计练习题代写
The data below shows the average weight of varsity football players at the University of Texas for selected years. Fit a linear model of the form (use R code given in Lecture Notes, no need to do by hand)
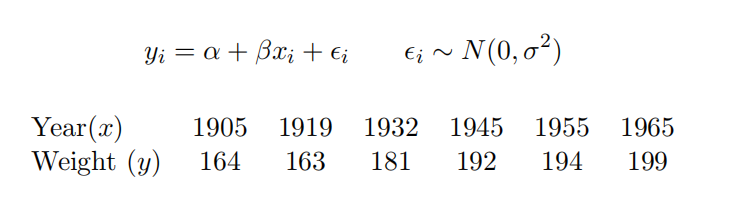
a) Find a 95% confidence interval for β.
b) Test the hypothesis H0: β = 0 versus H1: β ≠ 0 at α = 0.
c) Make the ANOVA table using the anova command in R and know what each number in the table means. What is the estimate for σ2?


