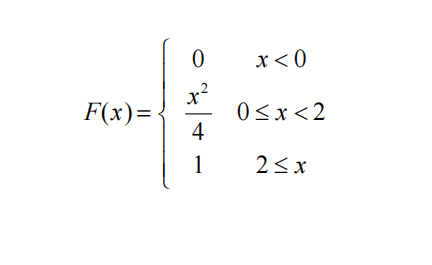HW
Q1)
The current in a certain circuit as measured by an ammeter is a continuous random variable X with the following density function:
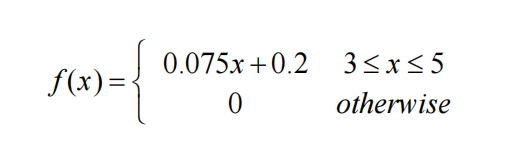
a. Graph the pdf and verify that the total area under the density curve is indeed 1.
b. Calculate P(X ≤ 4). How does this probability compare to P(X < 4)?
c. Calculate P(3.5 ≤ X ≤ 4.5) and also P(4.5 < X).
Q2)
“Time headway” in traffic flow is the elapsed time between the time that one car finishes passing a fixed point and the instant that the next car begins to pass that point. Let X = the time headway for two randomly chosen consecutive cars on a freeway during a period of heavy flow. The following pdf of X is essentially the one suggested in “The Statistical Properties of Freeway Traffic” (Transp. Res., vol. 11: 221–228):
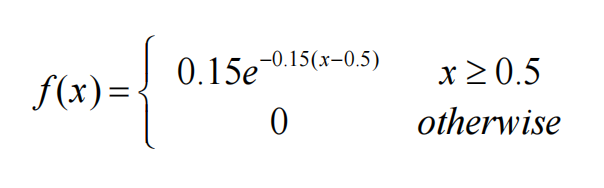
What is the probability that time headway is
a. At most 6 sec?
b. More than 6 sec? At least 6 sec?
c. Between 5 and 6 sec?
Q3) 统计概率作业代写
Let X denote the amount of time a book on two-hour reserve is actually checked out, and suppose the cdf is
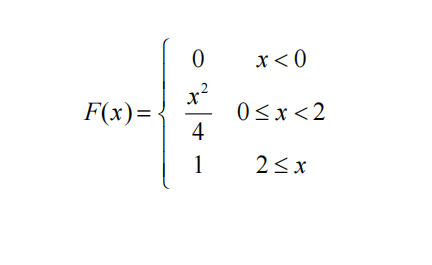
Use the cdf to obtain the following:
a. P(X ≤ 1)
b. P(.5≤ X ≤1)
c. P(X > 1.5)
d. The median checkout duration 𝜇̃ [solve 0.5 = F(𝜇̃)]
e. F'(x) to obtain the density function f(x)
f. E(X)
g. V(X) and 𝜎X
h. If the borrower is charged an amount h(X) = X² when checkout duration is X, compute the expected charge E[h(X)].
Q4)
Exercise 2 introduced the concept of time headway in traffic flow and proposed a particular distribution for X = the headway between two randomly selected consecutive cars (sec). Suppose that in a different traffic environment, the distribution of time headway has the form
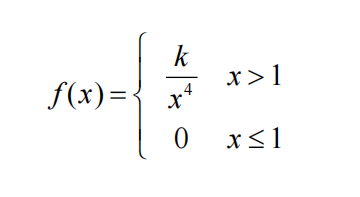
a. Determine the value of k for which f(x) is a legitimate pdf.
b. Obtain the cumulative distribution function.
c. Use the cdf from (b) to determine the probability that headway exceeds 2 sec and also the probability that headway is between 2 and 3 sec.
d. Obtain the mean value of headway and the standard deviation of headway.
e. What is the probability that headway is within 1 standard deviation of the mean value?
Q5) 统计概率作业代写
Let X have a uniform distribution on the interval [A, B].
a. Obtain an expression for the (100p)th percentile.
b. Compute E(X), V(X), and 𝜎X.
c. For n, a positive integer, compute E(𝑋n).
Q6)
Determine 𝑧α for the following:
a. 𝛼 = 0.0055
b. 𝛼 = 0.09
c. 𝛼 = 0.663
Q7) 统计概率作业代写
In a road-paving process, asphalt mix is delivered to the hopper of the paver by trucks that haul the material from the batching plant. The article “Modeling of Simultaneously Continuous and Stochastic Construction Activities for Simulation” (J. of Construction Engr. and Mgmnt., 2013: 1037-1045) proposed a normal distribution with mean value 8.46 and standard deviation 0.913 min for the rv X = truck haul time.
a. What is the probability that haul time will be at least 10 min? Will exceed 10 min?
b. What is the probability that haul time will exceed 15 min?
c. What is the probability that haul time will be between 8 and 10 min?
d. What value c is such that 98% of all haul times are in the interval from 8.46-c to 8.46+c?
e. If four haul times are independently selected, what is the probability that at least one of them exceeds 10 min?
Q8) 统计概率作业代写
Suppose that blood chloride concentration (mmol/L) has a normal distribution with mean 104 and standard deviation 5 (information in the article “Mathematical Model of Chloride Concentration in Human Blood,” J. of Med. Engr. and Tech., 2006: 25–30, including a normal probability plot as described in Section 4.6, supports this assumption).
a. What is the probability that chloride concentration equals 105? Is less than 105? Is at most 105?
b. What is the probability that chloride concentration differs from the mean by more than 1 standard deviation? Does this probability depend on the values of 𝜇 and 𝜎?
c. How would you characterize the most extreme 0.1% of chloride concentration values?
Q9) 统计概率作业代写
The automatic opening device of a military cargo parachute has been designed to open when the parachute is 200 m above the ground. Suppose opening altitude actually has a normal distribution with mean value 200 m and standard deviation 30 m. Equipment damage will occur if the parachute opens at an altitude of less than 100 m. What is the probability that there is equipment damage to the payload of at least one of five independently dropped parachutes?
Q10)
If bolt thread length is normally distributed, what is the probability that the thread length of a randomly selected bolt is
a. Within 1.5 SDs of its mean value?
b. Farther than 2.5 SDs from its mean value?
c. Between 1 and 2 SDs from its mean value?
Q11) 统计概率作业代写
The weight distribution of parcels sent in a certain manner is normal with mean value 12 lb and standard deviation 3.5 lb. The parcel service wishes to establish a weight value c beyond which there will be a surcharge. What value of c is such that 99% of all parcels are at least 1 lb under the surcharge weight?
Q12)
Suppose only 75% of all drivers in a certain state regularly wear a seat belt. A random sample of 500 drivers is selected. What is the probability that
a. Between 360 and 400 (inclusive) of the drivers in the sample regularly wear a seat belt?
b. Fewer than 400 of those in the sample regularly wear a seat belt?