TEST
经济统计网课代考 To obtain sample information, a survey is independently ad- ministered to 100 people asking them whether they are going to buy the mobile phone.
Q1 A multinational consumer electronics company is releasing a new mo- bile phone in a particular country, and would like to estimate consumer demand. 经济统计网课代考
To obtain sample information, a survey is independently ad- ministered to 100 people asking them whether they are going to buy the mobile phone. The survey revealed that 65 out of 100 would buy the mobile phone. Let θ denote the proportion of people who would buy the mobile phone. The goal is to estimate θ based on this sample information.
(a)Beforetaking into account sample information, the company’s belief about θ can be modelled by a Beta(α, β) Show that the posterior distribution of θ given the data is Beta(α + 65, β + 35). You do not need to evaluate any integrals or normalising constants. [4]
(b)Thecompany decides to model their prior beliefs about θ using a Beta distribution with a mean of 0.7 and standard deviation 0. Write down the parameters α and β of the Beta(α, β) distribution which represent this belief (you may want to look at the formula sheet). [2] 经济统计网课代考
(c)Write down the posterior distribution for θ using the above survey answersand the prior from part (b). [3]
(d)Givea point estimate for θ under squared error [2]
(e)Provethat the mode of a Beta(α, β) distribution is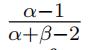 
and hence give a Bayesian point estimate for θ under the 0−1 loss function. [4]
Q2 An investment company wishes to model the daily log-returns of a financial stock. The following historical record is available:
Y1 = 0.42, Y2 = −0.49, Y3 = 0.21, Y4 = −0.42, Y5 = −0.56, Y6 = −0.2
Assume that daily log-returns are independent and identically dis- tributed draws from a Normal distribution with known mean 0 but unknown variance σ2.
Consider an alternative parametrization of the distribution of Yi:
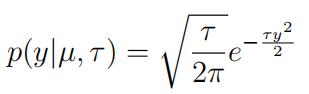
where τ is the precision parameter defined as the reciprocal of the variance σ2, i.e. 
(a)Usingthe Gamma(α, β) distribution as a conjugate prior for τ , de- rive the posterior distribution based on this historical You do not need to evaluate any integrals or normalising constants.[4] 经济统计网课代考
(b)Let Y˜denote the log-return on a particular day in the future. Show that the posterior predictive distribution is of the following form:
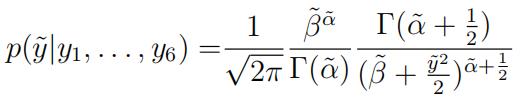
for some values of α˜ and β˜. Using the numeric values of Y1, . . . , Y6 provided above, give expressions for α˜ and β˜ in terms of α and β.State the set of possible values that Y˜can take. [7]
(b)Statethe Pickands Balkema de Haan theorem and explain why it may be of use in risk [4]
(c)Findthe probability of log-return on the following day, Y7, falling below 0.7 using a Generalised Pareto Distribution (GPD) with threshold u = 0. Use the method of moments to estimate the GPD parameters. [8]
(d)Discuss the strengths and weaknesses of modelling data in this context using a Normal distribution versusthe [3] 经济统计网课代考
(f)Considersome random variable X which has an exponential dis- tribution, i.e. X Exponential(λ). Given a threshold u, let Fu denote the distribution function of X conditional on X > u. In other words, for all z > u, we have Fu(z) = p(X ≤ z|X > u). Show that Fu(z) = 1 − e−λ(z−u). [4]
Q3 A financial company located on an island sells hurricane protection in- surance. 经济统计网课代考
In order to price this insurance product, the company wishes to build a statistical model for inter-arrival times between successive hurricanes. Let Y1, . . . , Yn denote the number of years between succes- sive hurricanes that hit the island. The company decides to model these as independent and identically distributed random variables following a Geometric(θ) distribution with the probability mass function:
p(Y = k|θ) = (1 − θ)k−1θ, k = 1, 2, 3 . . . θ ∈ [0, 1]
The company has access to the following historical record:
Y1 = 2, Y2 = 1, Y3 = 3, Y4 = 3, Y5 = 2, Y6 = 3
(a)Thecompany decides to model its beliefs about the probability of a hurricane occurring in any given year using a Beta distribution with a mean of 0.4 and standard deviation 0.2. Find the corre- sponding values of α and β for the conjugate Beta(α, β) prior that represent the company’s beliefs about θ. [2]
(b)Write down the posterior distribution for θ using the historical record and the prior from part (a), and clearly state itsparame- ters. [3] 经济统计网课代考
(c)LetY˜= 1, 2, 3, . . . denote the waiting time between two successive
hurricanes in the future. Derive the posterior predictive distribu- tion p(y˜ y1, . . . , y6) based on the historical record, and show that it has the following form:
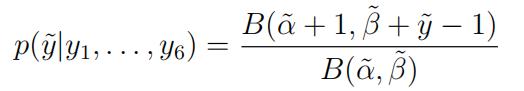
for some values of α˜ and β˜ that you should define. [4]
For the remainder of this question you can use the fact that the Beta function B(α, β) in the Beta distribution, is defined as:
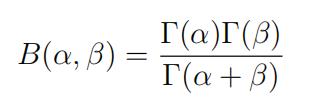
and that when n is a positive integer, Γ(n) = (n − 1)!.
(d)The company now suspects that there might have been a struc- tural change in the hurricane frequency due to climate change. Thisimplies that the change point has occurred immediately af- ter observation Y3 and the probability of a hurricane occurring in any subsequent year has Thus, observations Y4, Y5 and Y6 still come from a Geometric distribution but with a different parameter θ, i.e.:
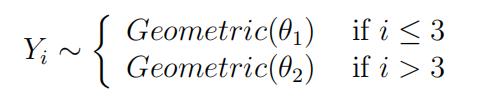
Define the two models:
M0 : There has been no change point in the hurricane frequency. M1 : There has been a change point in the hurricane frequency immediately after observation Y3.
Assuming that there have been no other change points, compute marginal likelihoods under both models p(y1, . . . , y6 Mi), and de- cide whether there has been a structural change in the hurricane frequency. Both models M0 and M1 are equally likely a priori. Note that you should use prior from part (a) in model M0, and for both segments in model M1. [16]
(e)Thereis evidence that there have been no change Now the company wishes to compare M0 model with an Exponential distri- bution model M2. The company assumes that it is fine to model the discrete number of years using the Exponential distribution for continuous random variables. 经济统计网课代考
Define the two models:
M0 : The observations are Yi ∼ Geometric(θ).
M2 : The observations are Yi i.∼i.d. Exponential(λ).
Compute the marginal likelihood p(y1, . . . , y6|M2) under model
M2 using Gamma(1, 1) prior. Making use of the marginal likeli-
hood under model M0 from part (d), decide which model is better supported by the data. Both models M0 and M2 are equally likely a priori. [5]
Q4 (a) Let Y i.∼i.d.Bernoulli(θ). It is of interest to estimate θ using the loss function 经济统计网课代考
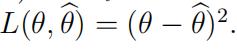Let the estimator be as follows:
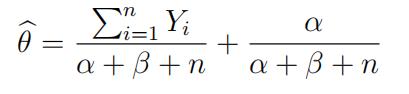
Compute the risk function, and find values of α and β for which θ^ is minimax. [8]
(b)Let
It is of interest to estimate σ2 using the loss functionL(σ2, bσ2 ) =(σ2 − bσ2)2 .
Let the estimator be as follows: 
Compute the risk function.[7]
(c) A car manufacturer is faced with the following two actions: a1 – advertise new model in various media, or a2 – do not advertise. The effectiveness of advertisement depends on the state of the economy: θ1 is “bad”, θ2 is “moderate”, and θ3 is “good”. 经济统计网课代考
The losses corresponding to each action ai, i = 1, 2, and type θj, j = 1, 2, 3, are represented by the following loss matrix :
| a1 | a2 | |
| θ1 | 1 | 0 |
| θ2 | 0.5 | 0.5 |
| θ3 | 0 | 1 |
Find the minimax randomized action. [5]
Q5 Let Yt =l n(Pt) l n(Pt−1) denote t he daily l og-return on a financial asset, where Pt i s the opening daily price at t ime t .
(a) The following model has been proposed to describe the behaviour of log-returns:
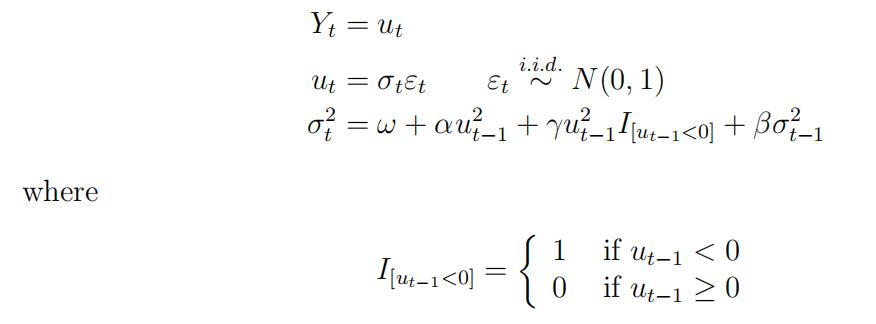
Derive the unconditional variance of Yt clearly showing all your steps. [6]
Q6 Consider the following information on the hypothetical portfolio of £10,000 invested in two assets.
The information on each daily asset return is provided in the table below. It is assumed that these returns are jointly normally distributed.
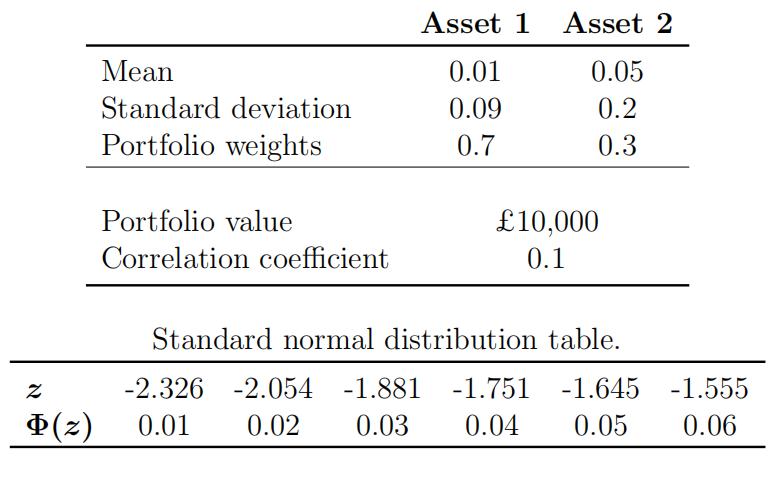
(i)Computethe 99% 1-day Value-at-Risk (VaR) of the portfolio in value Interpret your findings. [4] 经济统计网课代考
(ii)ConsiderABC Insurance company that wishes to measure its risk Let Lt denote independent and identically distributed annual aggregate losses that follow the exponential distribution with mean 10, i.e. E(Lt) = 10. Note that the losses are positive.
Compute the Expected Shortfall (ES0.99) which is defined as follows:
ES0.99 = E [Lt|Lt ≥ V aR0.99] [6]
更多代写：cs代上网课推荐 Cs北美代考 Critical Review Essay代写范文 Essay Claims代写 essays论文格式 统计网课托管
