Economics 3382A-001 Final Exam
经济学期末代写 Problem 1 (20 points) Each of 3 players chooses whether to contribute $1 toward provision of a public good. The good is provided if and only if all
120 minutes
PLEASE NOTE THAT ANSWERS WITHOUT EXPLANATION WILL NOT BE GIVEN FULL CREDIT
Problem 1 (20 points)
Each of 3 players chooses whether to contribute $1 toward provision of a public good.
The good is provided if and only if all players contribute. Contributions are never refunded to the players no matter how many players contributed. Each player receives benefit $4 if the public good is provided, and $0 if the public good is not provided. If a player contributes, then she pays the cost $1; if she does not contribute, then she pays no cost.
(a) (5 points) Find all rationalizable strategies for each player.
(b) (5 points) Find all pure strategy Nash equilibria.
(c) (10 points) Can you find a mixed strategy Nash equilibrium such that:
i. players 1 and 2 use the same mixed strategy: contribute with probability p, not contribute with probability 1 p (where 0 < p < 1);
ii. player 3 contributes with probability 1.
Explain your answer.
Problem 2 (25 points). 经济学期末代写
Consider the following sequential game between a police officer and a robber. First, the officer chooses whether to patrol the streets or not. Next, the robber observes the action chosen by the officer, and chooses whether to walk the streets or not. Payoffs depend on the chosen actions as follows:
| Officer \ Robber | Walk | Not walk |
| Patrol | 2, -2 | -1, 1 |
| Not patrol | -1, 1 | 0, 0 |
(a) (12 points) Solve the game by backward induction and write down your solution in terms of the players’s trategies.
Now suppose the players are allowed to choose mixed actions. First, the officer chooses probability p with which to patrol the streets. Choosing p means that the police officer will patrol the streets with probability p and not patrol with probability 1 – p. Next, the robber observes p, and chooses probability q with which to walk the streets. Choosing q means that the robber will walk the streets with probability q and not walk with probability 1 q.
Finally, the pure actions of both players are realized according to the chosen p and q. The payoffs depend on the realized pure actions as in the table above. Assume that the players choose their mixed actions to maximize their expected payoffs.
(b) (13 points) Solve the game by backward induction and write down your solution in terms of the players’s trategies.
Problem 3 (30 points). 经济学期末代写
Consider a two-player two-period game where each period the players play the following simultaneous move stage game:
| 1 \ 2 | L | R |
| U | 3, 0 | 1, 3 |
| D | 2, 0 | 1, 1 |
After the first period the players observe what was played in the first period. The payoff of each player is the sum of the payoffs from the two periods. Throughout the question restrict attention to pure strategies.
(a) (10 points) What is the highest possible payoff that player 1 can get in a subgame-perfect equilibrium of the entire game? Find any one such equilibrium.
(b) (10 points) What is the lowest possible payoff that player 2 can get in a subgame-perfect equilibrium of the entire game? Find any one such equilibrium.
(c) (10 points) Find all subgame-perfect equilibria that are providing player 2 with the lowest possible payoff as in part (b).
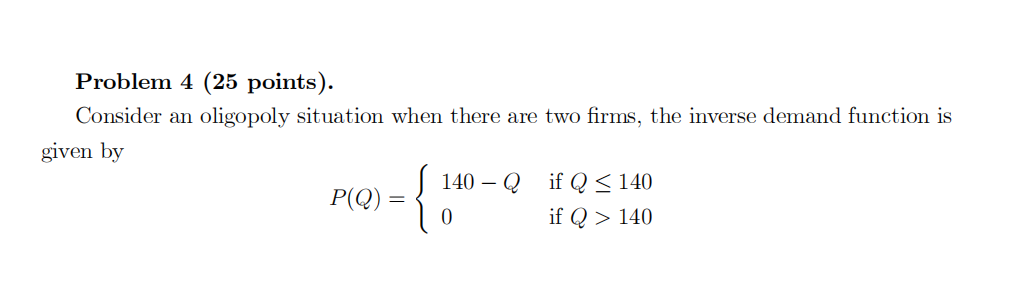
It is known that firm 1’s cost is equally likely to be high, CH(q) = 140q, or low, CL(q) = 0.
It is also known that firm 2 has low cost, CL(q) = 0. Firm 1 learns its cost before choosing its output. Firm 2 is aware of this fact but cannot itself observe firm 1’s cost. Both firms choose their outputs simultaneously. Throughout the problem you can assume that a firm with low cost produces positive quantity.
Find the (pure strategy) Nash equilibrium of this game. (Assume that the firm produces nothing if it cannot make strictly positive profits).

