线性偏微分方程代写 MATH704代写

MATH704 Linear Partial Differential Equations.

Problem Solving Questionnaire 1 Due on Friday 30 April 2021, 4 pm

线性偏微分方程代写 Start each question on a new page. Write thenumber of each question in the middle of a row.Do not copy the questions.

Attach this cover page to your questionnaire Do not attach any other covers

FAMILY NAME
First Name	线性偏微分方程代写
Student ID
Lecturer’s Name	Dr Farida Kachapova

Question	Marks possible	Marks given
1. 1)	2
2)	2
2	4
3. 1)	6
2)	3
4. 1)	6	线性偏微分方程代写
2)	3
5	6
6	9
7	9
8	10
9	10	线性偏微分方程代写
10	10
11	10
12	10
Total	100

Instructions: 线性偏微分方程代写

If you did not attempt a question, write 0 in the corresponding cell above.

Start each question on a new page. Write thenumber of each question in the middle of a row.Do not copy the questions.Show detailed working for each question, with solutions in order from the first question to the last question.

Solutions can be handwritten but legible. Highlight or frame final answers.

Submit your questionnaire online. Submission instructions are on Blackboard.

Students may discuss this questionnaire with the lecturer and other students. However, the entire student’s work must be their own. No student may receive any part of the questionnaire from another person, or let someone copy from their questionnaire. 线性偏微分方程代写

Failure to abide by this will result in the questionnaire not being accepted.

It is my responsibility to keep a copy of my questionnaire This questionnaire is entirely my own work S

ignature

Date

Question 1. 1) Separate the PDE u_xx 3u_t + 2u = 0 into a system of ODEs. 线性偏微分方程代写

2) Find all product solutions of this equation.

Question 2. Find all eigenvalues and eigenfunctions of the following eigenvalue problem:

X^jj + λX = 0, X^j(0) = X(1) = 0.

Question 3. 1) The temperature u(x, t) of a narrow metal rod of length L = π is modelled by the heat equation:

u_t = 9u_xx. 线性偏微分方程代写

Solve the equation if the initial temperature u(x, 0) = 2 cos x + 3 cos(3x), and the ends of the rod are insulated:

u_x(0, t) = u_x(π, t) = 0, t > 0.

2) Plot the answer from 1) in MATLAB as a surface u = u(x, t) in three-dimensional space. Include in your solution the Matlab code and picture of the surface.

Question 4. 1) Solve the following initial-boundary value problem modelling the vibration of a string with length L = 3 and fixed ends.

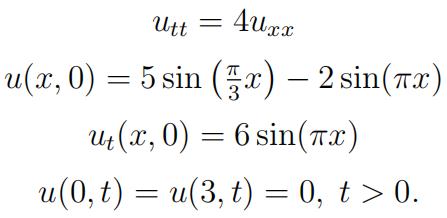
2) Plot the answer from 1) in MATLAB as a surface u = u(x, t) in three-dimensional space. Include in your solution the Matlab code and picture of the surface.

Question 5. The velocity potential of an incompressible flow satisfies Laplace equation: 线性偏微分方程代写

u_xx + u_yy = 0.

Solve the equation with the following boundary conditions:

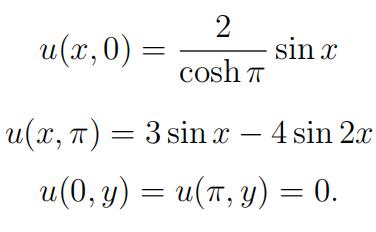
Question 6. The temperature u(x, t) of a narrow metal rod of length L = 1 is modelled by the heat equation:

u_t = 9u_xx

Solve the equation if the initial temperature u(x, 0) = 1, and the temperature at the ends is kept at 0 degrees:

u(0, t) = u(1, t) = 0, t > 0. 线性偏微分方程代写

Hint : find Fourier sine series for the function f (x) = 1 in the initial condition.

Question 7. Solve the following initialboundary value problem modelling the vibrationof a string with length L = 2 and fixed ends.

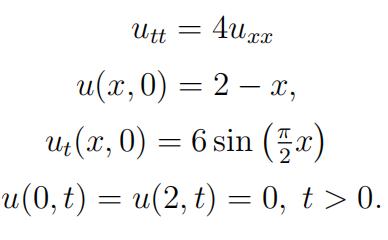
Question 8. The distribution of heat in a metal rod is modelled by the following non- homogeneous heat equation:

u_t = 2u_xx + 6 sin x.

Solve the equation if the initial temperature u(x, 0) = x, and the end temperatures are kept constant:

u(0, t) = u(π, t) = 0, t > 0.

Question 9. The following non-homogeneous heat equation 线性偏微分方程代写

u_t = 4u_xx + 2 − x

models the distribution of heat in a metal rod. Solve the equation if the initial temperature u(x, 0) = 2 − x, and the end temperatures are kept constant:

u(0, t) = u(2, t) = 0, t > 0.

Question 10. Solve the following initial-boundary value problem modelling the vibration of a string with length L = π and fixed ends.

u_tt = 4u_xx + x u

(x, 0) = 0

u_t(x, 0) = 3 sin x

u(0, t) = u(π, t) = 0, t > 0.

Question 11. The following non-homogeneous Laplace equation (Poisson equation) mod- els the distribution of electrical potential when an outside charge is present: 线性偏微分方程代写

u_xx + u_yy = 1 − x.

Solve the equation subject to the following boundary conditions:

u(x, 0) = u(x, 1) = 0,

u(0, y) = u(1, y) = 0.

Question 12. The temperature u(x, t) of a narrow metal rod of length L = π with a heat source is modelled by the following non-homogeneous heat equation:

u_t = u_xx + π − x.

Solve the equation if the initial temperature u(x, 0) = 2π + x + sin x, and the ends are kept at constant temperatures as follows:

u(0, t) = 2π, u(π, t) = 3π, t > 0.

Hint: Transform the non-homogeneous boundary conditions into homogeneous ones for w = u − c₁x − c₂.

合作平台：essay代写论文代写写手招聘英国留学生代写