ISyE/Math/CS/Stat 525 – Linear Optimization
Final exam
线性优化代写 No justifications needed. Mark “T” or “F”.Points per question: 0 points if wrong; 1/2 point if no answer; 1 point if correct.
READ THIS!
- This exam has a total of 4 problems and 40 points.
- Please write only one solution per question.
- The more clearly you write your answer, the better the chance that I can grade it accurately and give it full credit.
- Always justify your answers, unless otherwise stated.
- State properly any result that you use.
- Good Luck!
Question 1 线性优化代写
True or false …………………………………………………………. 10 points
No justifications needed. Mark “T” or “F”.
Points per question: 0 points if wrong; 1/2 point if no answer; 1 point if correct.

(b)_____
In the “column geometry” way of visualizing the simplex method, the reduced cost of variable xj is the vertical distance from the dual plane to the point (Aj , cj ).
(c)_____
The dual of min {c′x | Ax ≤ b, x ≥ 0} is max {p′b | p′A ≤ c′ , p ≤ 0}.
(d)_____
Different bases may lead to the same basic solution for the primal problem, but to different basic solutions for the dual.
(e)_____
If f is a flow vector that satisfies the flow conservation constraints, C is a cycle, and θ is a scalar, then f + θhC is also a flow vector that satisfies the flow conservation constraints.
(f)_____
The cost change resulting from the change of basis from f to f + θhC is given by c′hC .
(g)_____ 线性优化代写
Consider an uncapacitated network flow problem, and assume that the optimal cost is finite. If all supplies bi are integer, there exist an integer optimal flow vector, and an integer optimal solution to the dual problem.
(h)_____
Suppose that an algorithm takes polynomial time under the arithmetic model. Furthermore, suppose that on instances of size s, any integer produced in the course of the execution of the algorithm has size bounded by a polynomial in s. Then, the algorithm runs in polynomial time under the bit model as well.
(i)_____
The ellipsoid method solves the LP feasibility problem with integer data in polynomial time under the bit model.
(j)_____
Some LP problems with exponentially many constraint can be solved in polynomial time under the bit model.
Question 2 线性优化代写
The two-phase simplex method……………………………………….10 points
For two different linear programs (P1) and (P2) in standard form, during Phase I, we obtain the following tableaux (the original problem variables are x1, . . . , x4, and the artificial variables are y1, y2, y3).
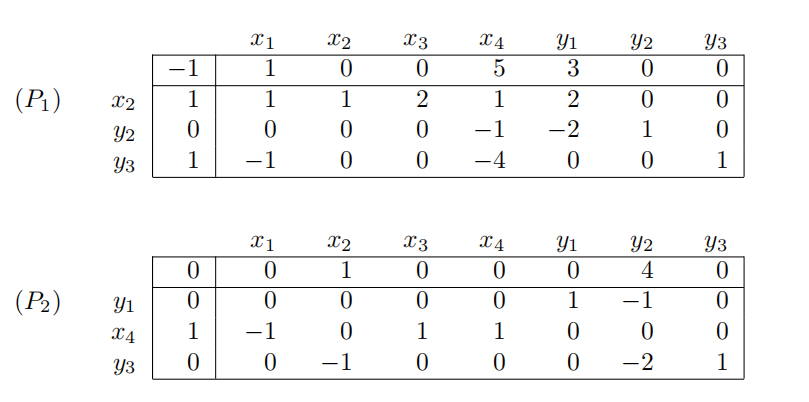
(a) (8 points) For each problem determine, if possible, a tableau to start Phase II, knowing that the objective function of both problems, to minimize, has coefffficients (2, 0, 0, 1).
__________________________________________________
__________________________________________________
__________________________________________________
(b) (2 points) Next, run the two-phase simplex method to termination by completing Phase II.
__________________________________________________
__________________________________________________
__________________________________________________
Question 3 线性优化代写
Duality proof ………………………………………………………… 10 points
Write a complete proof of Theorem 4.1: “If we transform the dual into an equivalent minimization problem and then form its dual, we obtain a problem equivalent to the original problem.” You can start with the following general linear programming problem as your primal:
min c′x
s.t. ai′x ≥ bi , i ∈ M1
ai′x ≤ bi , i ∈ M2
ai′x = bi , i ∈ M3
xi ≥ 0, i ∈ I1
xi ≤ 0, i ∈ I2
xi free, i ∈ I3
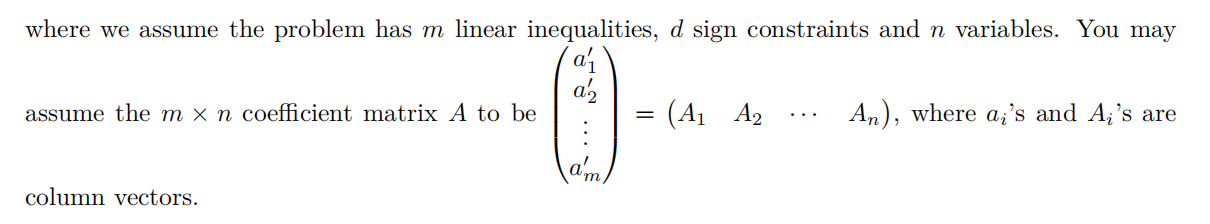
You should proceed by writing down the dual problem corresponding to the above one, then giving its equivalent minimization form of the dual, and writing down the dual of new minimization problem. You should briefly justify why these problems are equivalent as well.
__________________________________________________
__________________________________________________
__________________________________________________
Question 4 线性优化代写
Initial solution for network flow problems ……………………………. 10 points
In order to run the network simplex algorithm for an uncapacitated network flow problem, we need to obtain an initial basic feasible solution. In this exercise you will explain how such an initial basic feasible solution can be obtained. To answer this question, follow the three steps below briefly discussed in class, give all possible details, and justify every statement you make.
(a)(4 points) Construct an auxiliary directed graph by adding auxiliary arcs, and define the auxiliary problem over the new directed graph.
Hint: To define the auxiliary problem, in particular you need to define the costs of the arcs.
__________________________________________________
__________________________________________________
__________________________________________________
(b)(4 points) Explain how to obtain a basic feasible solution to the auxiliary problem without using the simplex method. (Don’t forget to prove that the solution you obtain is basic feasible!)
__________________________________________________
__________________________________________________
__________________________________________________
(c) (2 points) Explain how to obtain a basic feasible solution for the original problem from an optimal solution of the auxiliary problem.
__________________________________________________
__________________________________________________
__________________________________________________

其他代写: 英国代写 Exercise代写 finance代写 homework代写 北美作业代写 algorithm代写 analysis代写 app代写 assembly代写 C/C++代写 code代写 CS代写 cs作业代写 Data Analysis代写 essay代写
