Problems
线性代数课业代做 Instructions 1.Supply complete, rigorous solutions to each of the problems below.2.Cite the result or number when using a nontrivial
Instructions
- Supply complete, rigorous solutions to each of the problems below.
- Cite the result or number when using a nontrivial lemma/proposition/theorem from class or the readings.
- External textbooks or websites are not permitted.
1.True or false?
(a) A linear combination of surjective mappings V → V is again surjective.
(b) A linear combination of injective mappings V → V is again injective.
(c) If A,B are two linear mappings V → V, then AB = I implies BA = I. (Hint: V is allowed to be infinite-dimensional here.)
2. 线性代数课业代做
Recall what it means for two linear mappings A,B : V →V to be similar. If S is a set of linear mappings (or matrices), then S is similarity invariant if A ∈ S and A ∼ B implies B ∈ S.
Which of the following sets is similarity invariant?
(a) The set of invertible n×n matrices
(b) The set of diagonal n×n matrices
(c) The set of diagonalizable linear mappings V → V
(d) The set of nilpotent linear mappings V → V
(e) The set of symmetric n×n matrices
(f) The set of skew-symmetric n×n matrices
(g) The set of n×n matrices of finite order; i.e. those matrices such that Ak = I for some k.
(h) The set of n×n matrices with determinant equal to 1
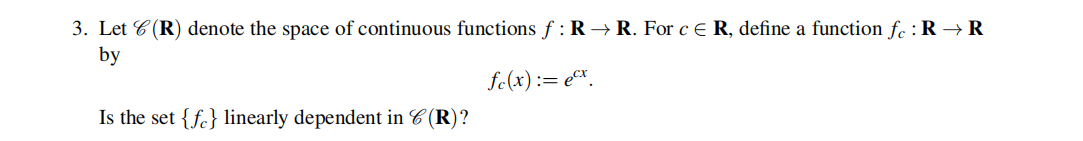
4.
Let V be a vector space. Prove that dim(V) < ∞ if and only if AB = I =⇒ BA = I for all linear mappings A,B : V → V.
5.Sums of subspaces.
(a) Let W1,W2 be two subspaces of a vector space V. Show that the union W1∪W2 may not be a subspace; in fact show that W1∪W2 is a subspace if and only W1 ⊆ W2 or W2 ⊆ W1.
Since the union of two subspaces isn’t a subspace, we need a different way to “combine” two subspaces …
(b) Complete the definition: the subspace sum of W1 and W2 is the set W1 +W2 = {··· }.
(c) Prove that W1 +W2 is a subspace of V; in fact show that it is the smallest subspace containing both W1 and W2.
(d) In R3 , let W := span{(1,0,−1)}. Find a subspace W′ such that R3 = W +W′.
(e) Let B1,B2 be bases for W1,W2. Show that B1∪B2 is a spanning set for W1 +W2, but may not be a basis.
(f) If U,W,X are three subspaces such that U + X = W + X, does it follow that U = W? Proof or counterexample.
(g) Suppose that V is finite dimensional and W1,W2 are subspaces of V. Find a formula relating the dimensions of W1 +W2, W1, W2, and W1∩W2.
6. 线性代数课业代做
We write V = W1⊕W2to mean that V = W1+W2 and W1 ∩W2 = {0}. This is called a direct sum.
(a) Prove that the following are equivalent for subspaces W1,W2 of a vector space V.
(i) W1∩W2 = {0}.
(ii) If w1 ∈ W1 and w2 ∈ W2 are nonzero vectors, then {w1,w2} is linearly independent.
(iii) If w1 +w2 = 0 for some w1 ∈ W1 and w2 ∈ W2, then w1 = w2 = 0.
(b) In R3 , let W := span{(2,1,0),(0,1,−1)}. Find a subspace W′ such that R3 = W⊕W′.
(c) Recall the following definitions: transpose of a matrix, symmetric matrix, and skew-symmetric matrix. Let Symn(K) and SkewSymn(K) be the sets of symmetric and skew-symmetric n × n matrices over K, respectively. Show that
Mn(K) = Symn(K)⊕SkewSymn(K).
(d) Suppose V = W1⊕W2. Show that if B1,B2 are bases for W1,W2, then B1 ∪B2 is a basis for V. 线性代数课业代做
This shows why it’s useful to break a vector space into a direct sum: it makes it easy to find a basis for V. Just find a basis for each part, then take the union to find a basis for V.
(e) Let V be finite-dimensional and suppose V = W1 +W2. Show that V = W1⊕W2 if and only if dim(W1) +dim(W2) = dim(V).
(f) Is (e) true if we don’t originally assume that V = W1 +W2? i.e. is the following statement true: “if W1,W2 are subspaces of V, then V = W1⊕W2 if and only if dim(W1) +dim(W2) = dim(V)”?

8.Image and nullspace review. 线性代数课业代做
(a) Complete the definition: if T : V → V is a linear mapping, the image of T is the set
T(V) = im(T) = {··· }.
(b) Prove that im(T) is a subspace of V.
(c) Complete the definition: if T : V → V is a linear mapping, the kernel (or nullspace) of T is the set
ker(T) = null(T) = {··· }.
(d) Prove that ker(T) is a subspace of V.
(e) Prove that T is injective if and only if ker(T) = 0.
(f) Let T : V → V be any linear mapping. Prove that V = ker(T)⊕im(T).
9.Projections. 线性代数课业代做
These will be very important. A linear mapping P : V → V is a projection if P2= P.
(a) Give three different examples of projections R2 → R2 .
(b) Let n ≥ 1. For which k ∈ N does there exist a projection P of rank k? Give a comprehensive answer.
(c) Pete disagrees with your answer in part (a); he can show that in finite dimensions, the only projections are 0 and I. First, Pete observes that in the finite dimensional case we can assume that V is isomorphic to Kn and we can think of linear mappings as n×n matrices. So if P is an n×n matrix such that P2 = P, then P2 − P = 0, which factorizes as P(I − P) = 0. But this implies P = 0 or P = I, because a product of matrices is zero only if one of them is zero.
What is wrong with Pete’s proof?
10.
(a) Let W be any subspace of V. Show that there is always a projection P :V →V such that im(P) =W; thus P called a projection onto W. (Hint: find a basis for W, then extend it to V …)
(b) Let P,Q : V → be two projections. Is it true that if im(P) = im(Q), then P = Q?
(c) Let P,Q : V → be two projections. Show that rank(P) = rank(Q) if and only if P ∼ Q (i.e. P is similar to Q).

14.Let T : V → V be a linear mapping and let W be a subspace. Let P : V → V be a projection onto W, i.e. P2= P and im(P) = W.
Show that W is T-invariant if and only if T P = PT P.

16.Eigenvalues II.
(a) Let P3(R) be the space of polynomials of degree ≤ 3 with real coefficients, and let T : P3(R) → P3(R) be the differentiation operator. Find all eigenvalues of T.
(b) Same as (a), except with R replaced by C.
17.Eigenvalues III.
(a) Let T : V → V be a linear mapping. Show that λ is an eigenvalue for T if and only if the linear mapping T −λI is not injective.
(b) Show that T : V →V has an eigenvalue if and only if there is a 1-dimensional T-invariant subspace W of V.
(c) Show that if V is a finite-dimensional vector space over a field K, then every linear mapping T : V → V has at most finitely many eigenvalues. But show that there is an infinite-dimensional real vector space V and a linear mapping T : V → V which has every real number as an eigenvalue. (Hint for the second part: ecx.)

20.Let V be a finite-dimensional vector space and let T : V → V be a linear mapping. Show that if Tk= I for some k ∈ N, then T is diagonalizable.
21.Let T : V → W be a linear mapping.
(a) Show that T is surjective if and only if T has a right inverse, i.e. there is a linear map S : W → V such that T S = I.
(b) Show that T is injective if and only if T has a left inverse, i.e. there is a linear map S : W →V such that ST = I.
(c) Let T : V → V (so V = W). Show that T is injective if and only if T is surjective.
(d) Give a counterexample to show that (c) fails when V is infinite-dimensional; a good example is the vector space V = K N of infinite sequences with elements in K.
22.True or false? 线性代数课业代做
Let f : U → V and g : V → W be linear mappings.
(a) If f,g are isomorphisms, then so is g ◦ f .
(b) If g ◦ f is an isomorphism, then so are both f and g.
(c) If f,g are injective, then so is g ◦ f .
(d) If g ◦ f is injective, then so are both f and g.
(e) If f,g are surjective, then so is g ◦ f .
(f) If g ◦ f is surjective, then so are both f and g.
23.Let K be an uncountable field. Construct an uncountable set of matrices S ⊆ Mn(K) such that AB = BA for all A,B ∈ S and such that A2= I for all A ∈ S. Or, prove that no such set exists! What happens if K is countable (g. K = Q)?
24.Show that every invertible matrix has a square root. More precisely: if A ∈ Mn(K) is an invertible matrix, then there is a matrix B ∈ Mn(K) such that B2= A. (Assume K is algebraically closed and char(K) ≠2.)
25.Let A,B be square matrices of the same size. Show that if I − AB is invertible, then I − BA is also invertible.
26.Linear recurrences. 线性代数课业代做
This one is fun! Let K be a field and let KNdenote the set of functions x : N → K; we think of these functions as sequences of elements of K. We say that x ∈ KNis a linear recurrence if there exists d ≥ 1 and scalars c1,…, cd ∈ K such that the following relation holds for all n ≥ d:
x(n) = c1x(n−1) +···+cdx(n−d).
The simplest example of a linear recurrence is the Fibonacci sequence, which satisfies the recurrence relation x(n) = x(n−1) +x(n−2) (thus d = 2 for the Fibonacci sequence).
Let Lin(K) denote the set of linear recurrences x : N → K. In this problem, we will show that Lin(K) is a subspace of KN, which is a lot harder than it seems!
(a) Show that KN is a vector space over K (with pointwise operations).
(b) Let S : KN → KN be the shift map given by 线性代数课业代做
S(x)(n) := x(n+1).
Show that S is a linear mapping. Is it injective? Is it surjective?
(c) Show that if x is a linear recurrence, then so is S(x).
(d) For x ∈ KN, define a subspace V(x) of KN by
V(x) := spanK{x,S(x),S2(x),…}.
Show that V(x) is S-invariant. Show that x is a linear recurrence if and only if V(x) is finite-dimensional.
(e) Let x ∈ KN. Show that x is a linear recurrence if and only if there is an S-invariant subspace W of KN such that x ∈ W.
(f) Use (e) to prove that Lin(K) is a subspace of KN; thus a linear combination of linear recurrences is again a linear recurrence.
27.
Is every monic polynomial the characteristic polynomial of some matrix? If two matrices have the same characteristic polynomial, must the matrices be similar?

33.Can you find a 5×5 nilpotent matrix of nilpotency index 6? In general, can you find an n×n nilpotent matrix of nilpotency index k, where k > n?
34.Let A,B be commuting nilpotents. Prove that A+B and AB are both nilpotent.
35.
Let Nil(V) denote the set of nilpotent transformations V → V and let GL(V) be the set of of invertible transformations V → V.
(a) Is Nil(V) a subspace of End(V)? Is Nil(V) closed under composition?
(b) Is GL(V) a subspace of End(V)? Is GL(V) closed under composition?
(c) What is Nil(V)∩GL(V)?
36.Let A and B be two commuting nilpotents. Prove that A+B and AB are both nilpotent.
37. 线性代数课业代做
Show that a nilpotent transformation can only have 0 as an eigenvalue. (Hint: If T(v) = λv, then T2(v) = λ2v …)
38.(a) Let T : V → V be a transformation of a vector space V over an algebraically closed field K. Prove that if the only eigenvalue of T in K is zero, then T is nilpotent. (Hint: what kind of matrix will you get if you triangularize?)
(b) Is (a) true if K is not algebraically closed? Proof or counterexample.
39.Let T : V → V be a linear mapping of an n-dimensional vector space.
(a) Show that if T is triangularizable, then T has invariant subspaces of every dimension: i.e. there are T-invariant subspaces W1,…,Wn of V so that dim(Wi) = i for all 1 ≤ i ≤ n. (Notice that this appears to be weaker than the existence of a flag.)
(b) Is the converse of (a) true? Proof or counterexample.
40. 线性代数课业代做
Let T : V → V be a linear mapping of a finite-dimensional vector space V, and let W be a T-invariant subspace of V. Let T|W: W → W be the restriction of T to W. Prove that the characteristic polynomial of T|W divides the characteristic polynomial of T.
41.Let S,T : V → V be two linear mappings, and let W be a subspace of V which is both S-invariant and T-invariant. Show that W is invariant for both S+T and ST.
42.Let V be a finite-dimensional vector space.
(a) Let W1,W2 be two subspaces of V. Fill in the following formula (with proof):
dim(W1 +W2) = dim(W1) +dim(W2)−[something]
(b) Find a similar formula for three subspaces:
dim(W1 +W2 +W3) = ···
(c) How do these dimension formulas generalize for sums of k subspaces?


45.
Let V be finite-dimensional. Let T : V →V be a linear mapping such that Tn= I for some n ≥ 1; we say that T is a mapping of finite order. Show that W is a T-invariant subspace of V, then V = W⊕W′ for some T-invariant subspace W′ .
(You might want to come back to this after we learn inner products.)
46.Let T : V → V be a linear mapping and let W be a T-invariant subspace of V. Prove that if T is triangu-larizable then so is T|W.
47.Let U,N ∈ Mn(K) be matrices where U is invertible and N is nilpotent. It is well-known that U +N is guaranteed to be invertible. Or wait, was it nilpotent? Shoot, I forgot. Figure it out and supply a proof.
48.Understanding cyclic vectors. 线性代数课业代做
Let T :V →V be a linear map and let x ∈V. Let Z be the cyclic subspace generated by x:
Z(x) = span{x,T(x),T2(x),…,}.
(a) Show that Z(x) is T-invariant.
(b) Show that there exists k ≥ 1 so that B = {x,T(x),…,Tk(x)} is a basis for Z(x).
(c) Let B be as in (b). Suppose Tk+1(x) = 0; what’s nice about [T|Z(x) ]B? Even if Tk+1(x) ≠ 0, the matrix [T|Z(x) ]B is still pretty nice — why?
49.Let T : V → V with V finite-dimensional.

50.Let T : V → V with V finite-dimensional. Suppose Tr(Ti) = 0 for all i. Prove that T is nilpotent.
51.
Let A,B ∈ Mn(K). Let us write A ∼KB to mean that there is an invertible matrix P ∈ Mn(K) such that PAP−1= B; you can prove that ∼K is an equivalence relation. Determine, with proof, which of the following statements is true.
(a) Let A,B ∈ Mn(R). If A ∼R B then A ∼C B.
(b) Let A,B ∈ Mn(R). If A ∼C B then A ∼R B.
(c) Let A,B ∈ Mn(Q). If A ∼Q B then A ∼R B.
(d) Let A,B ∈ Mn(Q). If A ∼R B then A ∼Q B.
52.(a) Let A ∈ M3(Q) be a 3×3 matrix with eigenvalues λ = 1,2,3. Express A−1 as a linear combination of powers of A.
(b) More generally: let T : V → V be a linear map with dim(V) < ∞. Show that if T is invertible, then T−1 is a linear combination of powers of T.
53.Division algorithm for polynomials. 线性代数课业代做
Let f(x),g(x) ∈ F[x] be two polynomials over a field F with g(x) ≠0. Show that there exist polynomials q(x),r(x) ∈ F[x] such that
f(x) = g(x)q(x) +r(x)
and deg(r(x)) < deg(g(x)). (Note: the degree of a constant polynomial is zero, with the exception of the zero polynomial; by convention, the degree of the zero polynomial is −∞!)
The strategy is remarkably identical to the proof used for integers. Define a set of polynomials S by
S = {r(x) ∈ F[x] : there exists q(x) ∈ F[x] such that r(x) = f(x)−g(x)q(x)}.
Then S is nonempty. So by well-ordering, we can select an element r(x) ∈ S of least degree. Now argue that this r(x) is as required.

58.
Let T : V → V be a linear mapping of a finite-dimensional vector space V. Let Wi= ker(Ti).
(a) Show that we have a decreasing chain of subspaces W1 ⊇ W2 ⊇ W3 ⊇ ···.
(b) Show that the chain stabilizes: there is some i ∈ N so that Wi = Wi+1 = Wi+2 = ···. In fact show that we can take i ≤ dim(V).
(c) [Maryam] True or false? If Wi = Wi+1 for some i, then Wi = Wi+d for all d ≥ 1. (In plain language: if the chain stabilizes at some point, then the entire chain terminates at that point.)
59.Let F2= {0,1} be the field of two elements. Here we’ll use polynomials and matrices to construct a field with four elements.
(a) Give an example of a 2×2 matrix A ∈ M2(F2) whose minimal polynomial is x2 +x+1.
(b) Let F = {0,I,A,A2}. Show that F is a field (when equipped with usual matrix addition and multiplication).
(c) Adapt this idea to construct a field of eight elements and a field of nine elements.
60. 线性代数课业代做
A matrix A ∈ Mn(F) has finite order if Ak= I for some k ∈ N. The smallest such integer k is called the order of A (not dissimilar from the definition of nilpotency index).
(a) True or false? If A is a matrix of order k, then mA(x) = xk −1.
(b) True or false? Every matrix of finite order is diagonalizable.
61.
Let L(V) denote the space of linear transformations T : V → V. For S,T ∈ L(V), the Lie bracket of S and T is
[S,T] := ST −T S.
For T ∈ L(V), define a linear mapping ad(T) : L(V) → L(V) by
ad(T)(S) = [T,S].
This is called the adjoint representation of T.
(a) True or false? If ad(T) = ad(S), then T = S.
(b) Show that ad : L(V) → L(L(V)) is a linear mapping.
(c) Prove that [ad(S), ad(T)] = ad([S,T]).
(d) Prove the product rule: ad(T)([X,Y]) = [ad(T)(X),Y] +[X, ad(T)(Y)].
(e) True or false? If T is nilpotent, then ad(T) is nilpotent.
(f) True or false? If T is diagonalizable, then ad(T) is diagonalizable.
(g) Show that if T = D+N is the Jordan–Chevalley decomposition of T, then ad(T) = ad(D) +ad(N) is the Jordan–Chevalley decomposition of ad(T).
62. 线性代数课业代做
Let W be a subspace of V. A complement for W is a subspace W′ such that V = W⊕W′ .
(a) Show that every subspace has a complement. Is the complement necessarily unique?
(b) Suppose V is finite-dimensional over an algebraically closed field F, and let T : V → V be a linear mapping. Prove that T is diagonalizable if and only if every T-invariant subspace of V has a T-invariant complement.
(c) Does (b) remain true if we remove the assumption that F is algebraically closed? Proof or counterexample.
63. 线性代数课业代做
Let T : V → V be a linear mapping of a finite-dimensional vector space V and let W be a T-invariant subspace of V. If T|Wis diagonalizable, does it follow that T is diagonalizable? What if we replace “diagonalizable” with“triangularizable”?
64.A linear mapping T : V → V satisfies the following criteria. Deduce, with proof, the Jordan form of T and the corresponding dot diagram.
pT(x) = x2(x−1)3(x−2)4 , mT(x) = x(x−1)2(x−2)2 , dim(E2) = 2.
65.Let T : V → V be a linear mapping with dim(V) = 7, rank(T) = 2, and suppose that T has exactly three distinct eigenvalues. Prove that T is diagonalizable.
66.Find, with proof, all n ∈ N for which the following statement is true.
If A,B ∈ Mn(C) are two nilpotent matrices with the same rank and same nilpotency index, then A ∼ B.

69.Preduals. Let V be an F-vector space. A predual for V is an F-vector space W such that W∗ ≃ V.
Which of the following vector spaces have preduals?
R R2

