MTH 342 Final Exam
线性代数考试代考 Instructions Put your work on separate pieces of paper. (There is not enough room for your answers on these pages!) You will be submitting your
Instructions 线性代数考试代考
Put your work on separate pieces of paper. (There is not enough room for your answers on these pages!) You will be submitting your work to Gradescope as a variable length submission. Follow the instructions posted on Canvas for the final exam.
Make sure that what you submit is neat and legible. Show your work on these problems. Points may be deduced for sloppy work.
You may not discuss this exam with anyone, except the TA and myself. The exam is open book, open notes. Specifically, this means you can use the material posted on Canvas, your graded work on Gradescope, the textbook, and your notes, but no other resources.
Notation 线性代数考试代考
- Pn= Pn(C) denotes the vector space of polynomials of degree ≤ n with complex coefficients.
The final exam problems begin here.
1.
The standard inner product on the vector space Cn is
(x, y) = y∗x.
Briefly explain why the standard inner product is defined as y ∗x instead of y T x.
Hint: consider the properties of the norm (length) induced by an inner product.

3.
Let D be an n × n diagonal matrix with complex entries. Which of the following must be true about D?
For each statement, spell out ‘True’ or ‘False’ on the pages that you submit to Gradescope. Select ‘True’ if it must be true; select ‘False’ otherwise. Give a brief explanation of your choice.
(a) D is lower-triangular
(b) D is upper-triangular
(c) D is invertible
(d) D = DT
(e) D is self-adjoint: D = D∗
(f) the eigenvalues of D are all distinct
(g) the eigenvalues of D are real
(h) for each eigenvalue of D its geometric multiplicity is equal to its algebraic multiplicity
(i) D can contain a row of zeros.

5.
Suppose A is an n × n matrix such that A∗ = −A.
(a) Give an example of such a matrix.
(b) Prove that the eigenvalues of A are purely imaginary complex numbers.
Hint: see Problem #3 on Worksheet 19 (and solutions).
6.
Consider the following matrices:
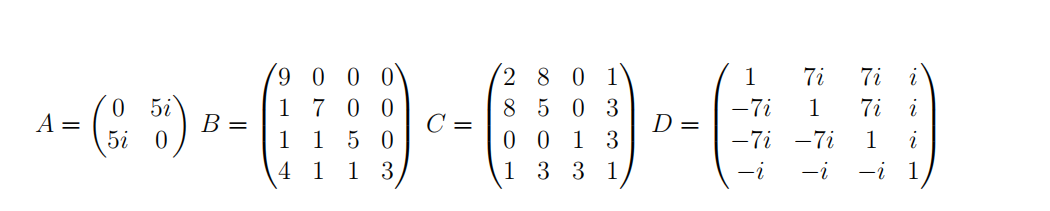
(a) Note any special structure that these matrices have.
(b) Some of the matrices A, B, C, D have the property that all of their eigenvalues are real. Which ones? For those that have all real eigenvalues, brieflfly explain why, using what you noted in part (a), and without doing any computations.
7.
We want to use linear algebra to find an equation of the line that best fits the data:
{(−1, −1), (0, 1), (1, 1), (2, 2)}.
The best fitting line is the least squares solution, which minimizes the following sum of squared differences:
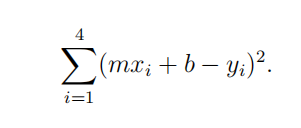
(a) Find equations your data would fit if there were an exact solution.
(b) Write these equations as a linear system in a matrix form.
(c) Identify A, x, and b, from part (b).
(d) Write the normal equation.
(e) Solve the normal equation and write an equation for the best fitting line (the least squares solution).
8.

(a) Find a 7 × 12 matrix C whose null space is isomorphic to Z4×3. In other words, find a matrix C so that
ker C ≌ Z4×3.
Note that ker C is a subspace of R12, but this subspace is isomorphic to Z4×3.
The matrix C must come from the defining properties of the subspace Z4×3. Do not ‘reverse engineer’ this problem by using information given below.
(b) Using Matlab, we find that the reduced row echelon form of C has 6 pivot columns (Matlab command: rref(C)). Explain how to use this fact (there are six pivot columns) to find the dimension of Z4×3.
(c) What is the dimension of Z4×3?
(d) Find a basis for Z4×3.
(Note: do not try to find an orthogonal basis. This is not possible anyway, because no inner product has been defined.)

