MATH 2006-R01-Linear Algebra-CRN 43816
Final Exam
Total points: 60
线性代数考试代写 1.(3 pts. each) True or false. Brieflfly explain your reasoning for each of the following.(a) Consider the linear system
Instructions: Write your answer neatly and show all the steps. Please submit your solutions as a single pdf document and upload it to Gradescope by the due date and time, (if you have diffiffifficulty in submitting to Gradescope then email me the fifinal to [email protected]).It is important that you show your work and use the notation that we have used in class. I will read through your proofs very carefully, so make sure you do not skip details.
Make sure your handwriting is big enough and legible. Also, make sure the pdf you are uploading is clear and readable.You will not receive any points if I cannot read your work clearly.
Do not cheat!Any potential cheating will be reported to Dean’s Offiffiffice; as a result, you may receive a 0 in this exam or an F in the course.You should NOT use any notes, textbook, calculator, or any other resources during the exam. Your fifinal submission MUST be written in your own words. It is unacceptable and unethical to look up the answers online or take anyone’s help.You must keep your video onthroughout the exam and you should NOT leave your seat without permission. You must submit the exam before leaving the zoom meeting room.
1.(3 pts. each) 线性代数考试代写
True or false. Brieflfly explain your reasoning for each of the following.
(a) Consider the linear system
a1,1x1 + a1,2x2 + · · · + a1,mxm = b1
a2,1x1 + a2,2x2 + · · · + a2,mxm = b2
·
·
·
an,1x1 + an,2x2 + · · · + an,mxm = bn
If the linear system has exactly one solution, then rank A < m.
(b) The following subset is a vector subspace of R2×3.
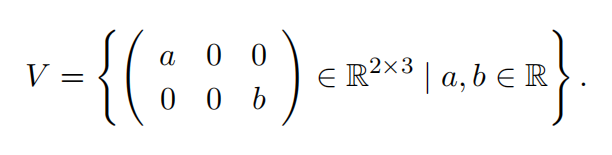
(c) If every vector in V can be written as a linear combination of the vectors in S = {v1, v2, · · · vn} in a unique way then S is linearly independent.
(d)Let C∞ be the vector space of infifinitely difffferentiable functions. The function T :C∞ → C∞ defifined by T(f(x)) = 3f − 4f‘(x) is a linear transformation.
2.(13 pts.) 线性代数考试代写
Let P2 denote the vector space of polynomials of degree at most 2. Let A ={ 1, x, x2} and B = {1, x − 1,(x − 1)2} be two bases for P3 and let T : P3 → P3 be the linear transformation defifined by T(p(x)) =p‘(x) + p(x).
(a) (4 pts.) Find the change of basis matrix SB→A from B to A.
(b) (5 pts.) Find the matrix of T with respect to the basis A.
(c) (2 pts.) Is T an isomorphism?
(d) (2 pts.) Without doing any computations, explain how you would compute the matrix of T with respect to the basis B by only using your responses in (a) and (b).
3.(13 pts.) 线性代数考试代写
Let T : R6 → R4 be the linear transformation given by the coeffiffifficient matrix

(a) (4 pts.) Find a basis for range(T).
(b) (5 pts.) Find a basis for ker(T).
(c) (2 pts.) State and verify the rank-nullity theorem.
(d) (2 pts.) With the above matrix A, is it possible to fifind a 6 × 4 matrix B so that the matrix BA is invertible? Brieflfly explain your answer.

(a) (2 pts.)Find the eigenvalues of A.
(b) (8 pts.) Find a basis for each eigenspace of A.
(c) (3 pts.) Find a diagonal matrix D and invertible matrix S such that AS = SD.


其他代写: assignment代写 finance代写 homework代写 java代写 matlab代写 python代写 report代写 paper代写 program代写 project代写 essay作业代写 作业代写 作业加急 英国代写 北美作业代写 加拿大代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写

