CSCI 3104 Summer 2021
Quiz 11
1 Instructions 算法quiz代做
- The solutions should be typed, using proper mathematical notation. We cannot accept hand-written solutions. Here’s a short intro to LATEX.
- You should submit your work through the class Canvas page only. Please submit one PDF file, compiled using this LATEX template.
- You may not need a full page for your solutions; pagebreaks are there to help Gradescope automatically find where each problem is. Even if you do not attempt every problem, please submit this document with no fewer pages than the blank template (or Gradescope has issues with it).
- You may not collaborate with other students. Copying from any source is an Honor Code violation. Furthermore, all submissions must be in your own words and reflect your understanding of the material. If there is any confusion about this policy, it is your responsibility to clarify before the due date.
- Posting to any service including, but not limited to Chegg, Discord, Reddit, StackExchange, etc., for help on an assignment is a violation of the Honor Code.
- You must virtually sign the Honor Code (see Section 2). Failure to do so will result in your assignment not being graded.
2 Honor Code (Make Sure to Virtually Sign the Honor Pledge) 算法quiz代做
Problem 1. On my honor, my submission reflects the following:
- My submission is in my own words and reflects my understanding of the material.
- I have not collaborated with any other person.
- I have not posted to external services including, but not limited to Chegg, Discord, Reddit, StackExchange, etc.
- I have neither copied nor provided others solutions they can copy.
In the specified region below, clearly indicate that you have upheld and agree to the Honor Code. Then type your name.
3 Standard 11- Network Flows: Reductions
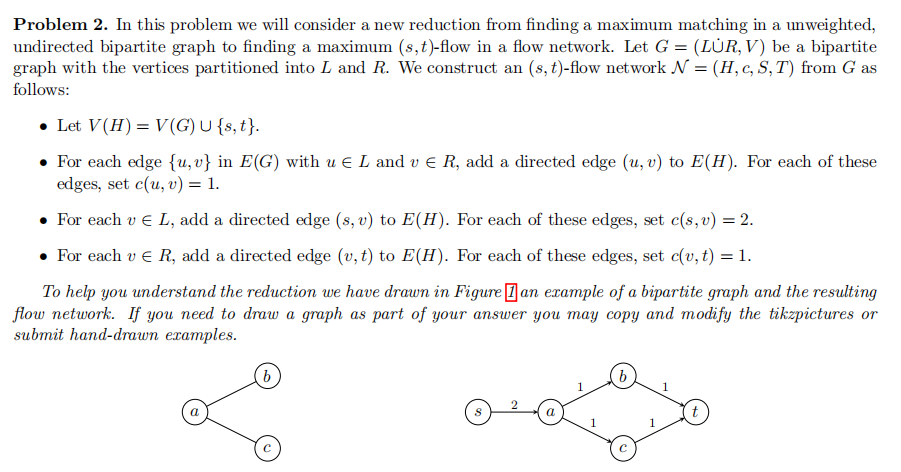
Figure 1: A bipartite graph and the flow network we get by applying the above reduction. The number next to each edge represents the capacity of that edge.
(a) Let M be a matching of G, where |M| = k. Is it the case that N has a feasible flow f where val(f) = k? If so, explain how to construct such a flow f from M. If not, carefully explain your reasoning.
(b) Let f’ be a feasible flow of N where for each edge (u, v) ∈ E(H), f’ (u, v) is an integer. Suppose that val(f’) = k. Does the existence of f’ imply that there is a matching M of size k in G? That is, can we necessarily recover a matching of size k of G from f’ ? If so, explain how to construct such a matching M from f’ . If not, carefully explain your reasoning.

更多代写:cs澳大利亚网课代修收费 GRE保分价格 英国影视类网课代做 澳洲统计学论文代写 北美Case Study代写 离散结构小考助攻
