算法问题集代写 CSCI 3104代写

CSCI 3104 problem set

算法问题集代写 Problem 1. Consider the interval scheduling problem from class. You are given a set of intervals I, where each interval has a start and end time

Instructions

The solutions should be typed, using proper mathematical notation. We cannot accept hand-written solutions. Here’s a short intro to LATEX.
You should submit your work through the class Canvas page only. Please submit one PDF file, compiled using this LATEX template.

Problem 1. 算法问题集代写

Consider the interval scheduling problem from class. You are given a set of intervals I, where each interval has a start and end time [s_i , f_i ]. Your goal is to select a subset S of the given intervals such that (i) no two intervals in S overlap, and (ii) S contains as many intervals as possible subject to condition (i).

Suppose we have two intervals with the same start time but different end times. That is, let I₁ = [s, f₁] and I₂ = [s, f₂] with f₂ > f₁.

(a) Let overlap([s, f]) denote the number of intervals of I (excluding [s, f]) with which [s, f] overlaps. Explain carefully why overlap(I₁) ≤ overlap(I₂).

(b) Suppose that overlap(I₁) < overlap(I₂). Explain carefully why I₂ can safely be exchanged for I₁.

Problem 2.

Consider the following graph G(V, E, w). Suppose we have the intermediate spanning forest F (indicated using thick edges) consisting of the edges {A, B}, {B, C}, and {C, D}. Clearly identify the safe, useless, and undecided edges. Justify your reasoning. [Hint: You may find Corollary 61 on page 42 of the typed lecture notes to be helpful.]

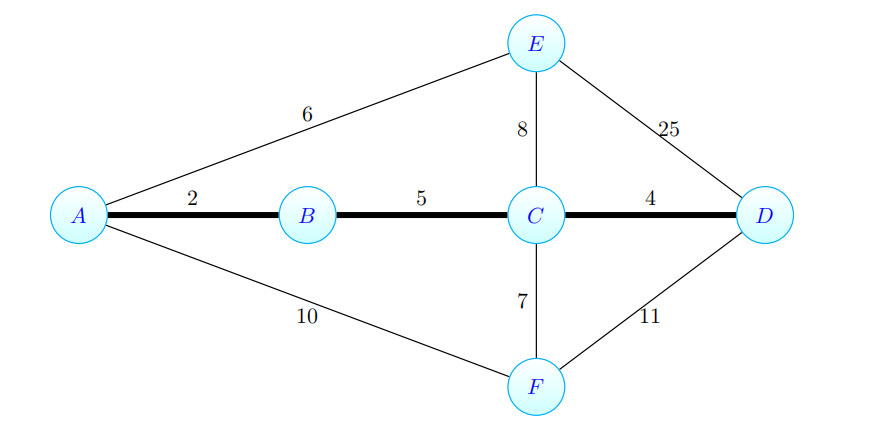
Problem 3.

Consider the following graph G(V, E, w). Clearly indicate the order in which Kruskal’s algorithm adds the edges to the minimum-weight spanning tree. You may simply list the order of the edges; it is not necessary to exhibit the state of the algorithm (i.e., the disjoint-set data structure) at each iteration.

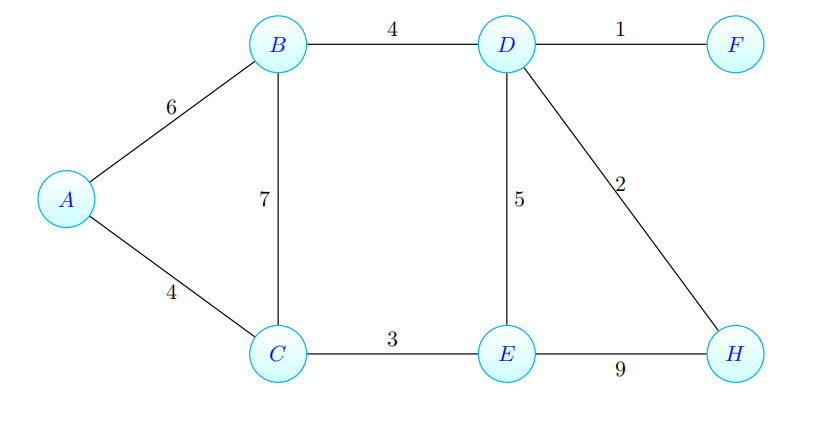
Problem 4. 算法问题集代写

Consider the following graph G(V, E, w). Clearly indicate the order in which Prim’s algorithm adds the edges to the minimum-weight spanning tree using H as the source vertex. You may simply list the order of the edges; it is not necessary to exhibit the state of the algorithm at each iteration.

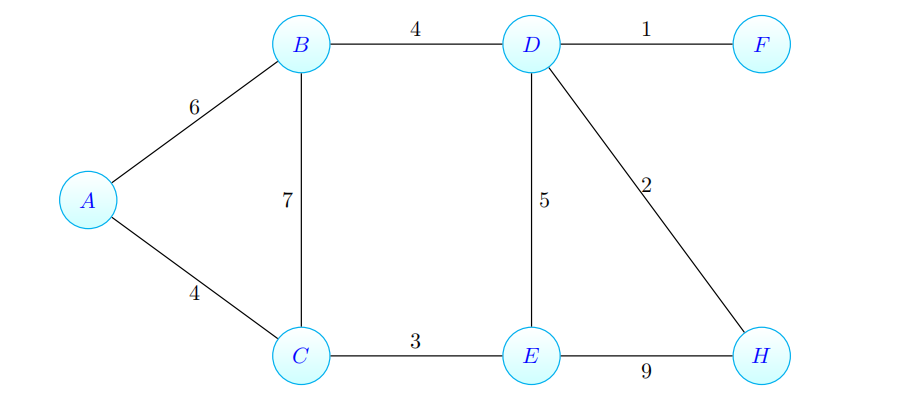
Problem 5. 算法问题集代写

We say that two i ～→ j paths are edge-disjoint if they do not share any common edges. Note however, these paths can (and in fact, often do) share common vertices (aside from i and j). As an example, consider the following graph.

Observe that 0 → 1 → 3 → 5 → 6 and 0 → 2 → 3 → 6 are edge-disjoint paths, as they do not share any directed edges. It is fine that they share the common vertex 3.
Note however that 0 → 2 → 4 → 6 and 0 → 2 → 3 → 6 are not edge-disjoint paths, as they both share the (0, 2) edge.

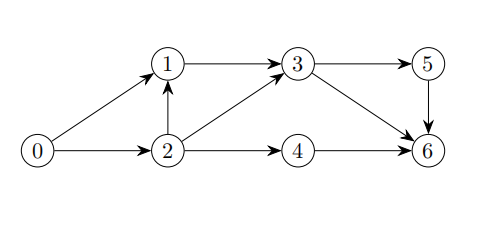
Consider the following problem.

Input: A directed graph G(V, E), as well as a start node i and an end node j.
Solution: We seek to find a set P of i → j paths such that any two distinct paths P₁, P₂∈ P are edge-disjoint, and |P| is maximum. That is, we seek to find a maximum set of edge-disjoint i → j paths.

(a) Describe how to reduce the above problem to the (one-source, one-sink) max-flow problem from class. Your description should be general, and not tied to a specific example.

(b) Using your reduction, find a maximum set of edge-disjoint paths from 0 ～→ 6 in the graph above. Show your work, as well as your final answer. Note that there may be multiple maximum-size sets P in the graph above; you need only find one such set P of edge-disjoint paths, as long as it has the largest number of paths possible.

Problem 6. 算法问题集代写

Let f(n) = 2³ⁿ and g(n) = n² . Determine the relationship that best applies: f(n) ∈ o(g(n)), f(n) ∈ O(g(n)), f(n) ∈ Θ(g(n)), f(n) ∈ ω(g(n)), or f(n) ∈ Ω(g(n)). Prove your answer.

Problem 7.

Let f(n) = n² and g(n) = n!. Determine the relationship that best applies: f(n) ∈ o(g(n)), f(n) ∈ O(g(n)), f(n) ∈ Θ(g(n)), f(n) ∈ ω(g(n)), or f(n) ∈ Ω(g(n)). Prove your answer.

合作平台：essay代写论文代写写手招聘英国留学生代写