CSCI 3104
Analyzing Code I: Nested Independent Loops 算法练习题代做
Problem. Analyze the worst-case runtime of the following algorithm. Clearly derive the runtime complexity function T(n) for this algorithm, and then find a tight asymptotic bound for T(n) (that is, find a function f(n) such that T(n) ∈ Θ(f(n))). Avoid heuristic arguments from 2270/2824 such as multiplying the complexities of nested loops. [Note: A[1, . . . , n][1, . . . , m] is a two-dimensional array with row indices in {1, . . . , n} and column indices in {1, . . . , m}.]
Assume that A[i][j] takes 2 steps, one for accessing A[i] and a second for accessing the jth element of A[i].
Algorithm 1 Nested Independent Loops
1: procedure Foo1(A[1, . . . , n][1, . . . , n]) 2: for i ← 1;i ≤ n;i ← i + 1 do 3: for j ← 1; j ≤ n; j ← j + 1 do 4: for k ← 1; k ≤ n; k ← k ∗ 2 do 5: if A[i][k] + A[k][j] ≤ A[i][j] then 6: print A[i][j]
Analyzing Code II: Nested Dependent Loops 算法练习题代做
Problem. Analyze the worst-case runtime of the following algorithm. Clearly derive the runtime complexity function T(n) for this algorithm, and then find a tight asymptotic bound for T(n) (that is, find a function f(n) such that T(n) ∈ Θ(f(n))). Avoid heuristic arguments from 2270/2824 such as multiplying the complexities of nested loops.
Algorithm 1 Nested Dependent Loops
1: procedure Foo1(Integer n) 2: for i ← 1;i ≤ 2 ∗ n;i ← i + 1 do 3: for j ← 1; j ≤ i; j ← j + 1 do 4: print (i + j)
Analyzing Code III: Writing Recurrences
Problem 2. Write down a recurrence for the runtime complexity of this algorithm. Clearly justify your answer.
You are not being asked to solve the recurrence.
Algorithm 1 Recurrences
1: procedure Foo1(Integer n) 2: if n < 5 then return 3: Foo1(n/5) 4: Foo1(n/5) 5: Foo1(n/5) 6: 7: for i ← 1;i ≤ 2 ∗ n;i ← i ∗ 3 do 8: print (i + j)
Unrolling 算法练习题代做
Problem. Using the unrolling method, find a suitable function f(n) such that T(n) ∈ Θ(f(n)). Show all work.
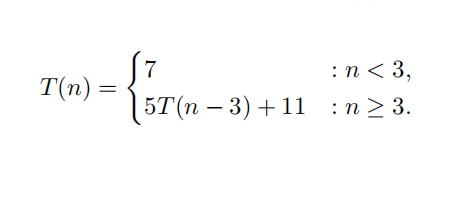
Tree Method
Problem. Using the tree method, find a suitable function f(n) such that T(n) ∈ Θ(f(n)). Show all work.
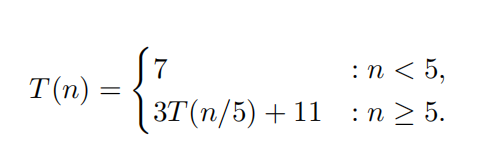
Divide and Conquer Principles 算法练习题代做
Problem. Given an array A[1, …, n], we say it contains a duplicate if there are two distinct indices i ≠ j such that A[i] = A[j]. Consider the following divide and conquer algorithm for counting the number of duplicates.
countDuplicates (A, p, q):
if q > p {
r = floor ((p+q)/2)
L = countDuplicates (A, p, r)
R = countDuplicates (A, r+1, q)
return L + R
}
else {
return 0
}
Will the above algorithm return the correct number of duplicates? Explain and justify your answer. If the algorithm does not perform correctly, give an example to illustrate that the algorithm fails.
Quicksort: Analysis 算法练习题代做
Problem. Assume that at each partitioning of a subarray of size n, you always get two subarrays of size 10 and size n−11, respectively. [Note that the pivot is not in either sub-array, so 10 and n−11 are indeed correct.] What would be running time of the resulting QuickSort algorithm? Use a suitable asymptotic notation to represent the running time, and explain/justify your answer.
Quicksort: Applications
Problem 2. Recall the Quickselect algorithm from PS10. [Note: For your convenience, we include the description of Quickselect on the next page.]
Do the following. Consider the initial input array A = [3, 7, 2, 9, 1, 6, 8, 4]. In the first call to Quickselect, the algorithm partitions A as follows:
A = [3, 2, 1|4|7, 6, 8, 9],
where left = [3, 2, 1] and right = [7, 6, 8, 9]. Suppose we are looking for the 2nd smallest element. Determine the recursive call to Quickselect. If the algorithm will instead return the pivot, state that. Explain your reasoning.
Dynamic Programming: Identify Precise Subproblems 算法练习题代做
Problem. Suppose we have n stairs to climb. In a single jump you may choose to jump up either 1, 2, or 3 stairs. Your goal is to count the total number of different ways to jump the n stairs. Note that your starting position is on the ground floor (stair 0) and not on the first stair. Clearly identify the precise sub-problems to consider. That is, what is the recursive structure to leverage when designing a dynamic programming algorithm?
DP: Write Recurrence 算法练习题代做
Problem. Suppose we can send one of two signals: s1 or s2, where s1 takes one second to send and s2 takes two seconds to send. Assume there is no delay between signals. Construct a recurrence to count the number of signals we can send in n seconds. Make sure to include your base cases. Justify your recurrence.
Dynamic Programming: One-Dimensional Examples
Problem. Recall the Rod Cutting Problem from class.
- Instance: Let n ≥ 0 be an integer where n is the length of the rod,and let p1, p2, . . . , pnbe non-negative real numbers. Here, pi is the price of selling a rod of length i.
- Solution: The maximum revenue, which we denote rn, obtained by cutting the rod into pieces of integer lengths and selling the pieces.
For the original rod cutting problem that we see in class (when each cut is free), we have the following recurrence for computing rn:
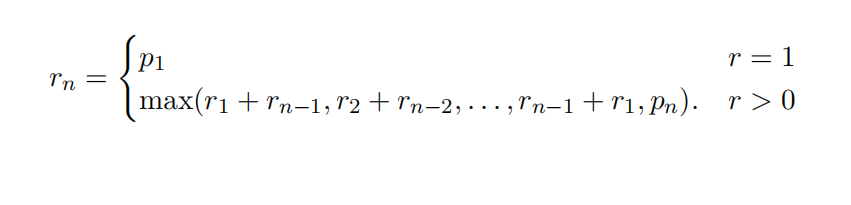
Do the following.
(a) Modify this recurrence to account for the fact that each cut costs $3 for our variant of rod cutting.
(b) Suppose we have a rod of length 6, with prices given as follows:
p1 = 1, p2 = 6, p3 = 8, p4 = 8, p5 = 9, p6 = 11.
Using a bottom-up dynamic programming approach, determine the maximum revenue r6 obtained by cutting up this rod under the assumption that each cut costs $3. For your convenience, we have provided the lookup table for you to use. You may also hand-draw your lookup tables.
| r1 | r2 | r3 | r4 | r5 | r6 |
Dynamic Programming: Two-Dimensional Examples 算法练习题代做
Problem. The Subset-Sum problem is defined as follows.
- Instance: We are given n items with weights w1, . . . , wn> 0, as well as a target threshold W > 0.


更多代写:cs澳洲包网课费用 在家考gre作弊 英国economic代写 北美MBA论文代写 北美report代写 算法问题集作业代写
