Project Grading Rubric
algorithm competition website代写 ata source and describeThe data came from kaggle, an algorithm competition website.The specific website
2018-11-26
Data source and describe algorithm competition website代写
The data came from kaggle, an algorithm competition website.The specific website is: https://www.kaggle.com/loganalive/echocardiogram-uci .This dataset consists of 132 instances of patients for 12 variables describing the patient’s heart attack and condition.I selected8 important variables as the data for this analysis, which are specifically described as follows:
1 survival: The number of months a person survived from heart disease was recorded. 2 still-alive: s the patient still alive? 0 means dead , 1 means still alive.algorithm competition website代写
- age:age in years when heart attack
- pericardial-e”usion:Pericardial e”usion is fluid around the 0=no fluid, 1=fluid.
- fractionalshortening:a measure of contracility around the heart ,lower numbers are increasingly
- epss: E-point septal separation, another measure of contractility. Larger numbers are increasingly algorithm competition website代写
- lvdd:left ventricular end-diastolic Large hearts tend to be sick hearts. 8 wall-motion-index: a measure of how the segments of the left ventricle are movin
Question algorithm competition website代写
All the patients had experienced heart attacks in the past.Some are still alive, some are dead for a shorttime.I want to know which variables have an important e”ect on this di”erence in outcome.Pericardiale”usion is a response to damage to the parietal pericardium and can cause other complications.Whetherpericardial e”usion significantly a”ects the time of death in patients with heart disease.
#Load the required packages and data library(ggplot2) library(survival) library("survminer") echocardiogram<-read.csv(file="echocardiogram.csv")
#Data cleaning and variable selection echocardiogram<-na.omit(echocardiogram[,c(1:7,9)])

Variable analysis algorithm competition website代写
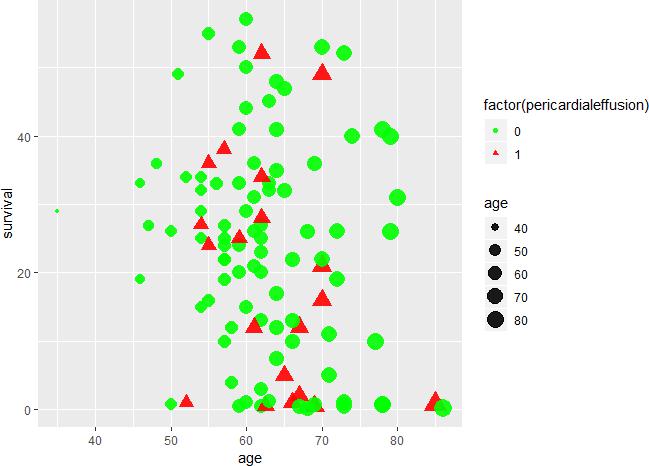
As can be seen from the figure below, there is no significant di”erence in survival time between patientswith pericardial e”usion and those without e”usion. The age of patients with pericardial e”usion is more concentrated, between 50 and 70 years old.
ggplot(echocardiogram, aes( x = age, y = survival, color = factor(pericardialeffusion), size = age, shape = factor(pericardialeffusion)))+ geom_point(alpha = 0.9)+ scale_color_manual(values=c('green','red'))
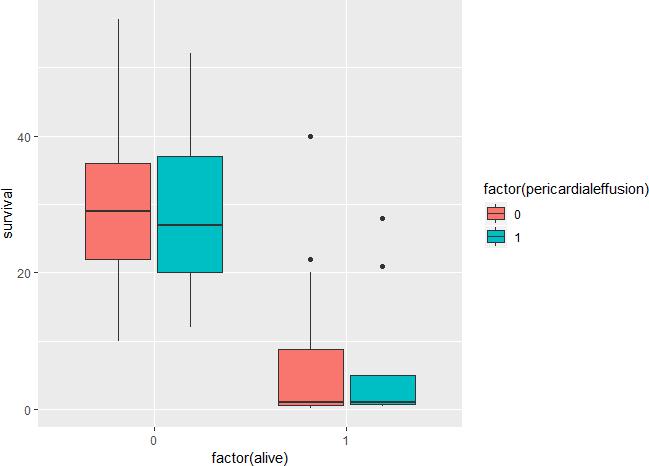
The following figure shows that the median survival month of patients with pericardial e”usion is lower than that of patients without pericardial e”usion in the surviving group.There was no significant di”erence between the median survival months in the death group.
ggplot(data=echocardiogram, aes(x=factor(alive),y=survival))+geom_boxplot(aes(fill=factor(pericard
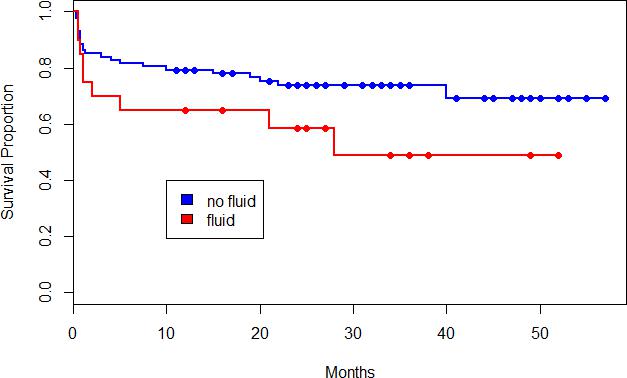
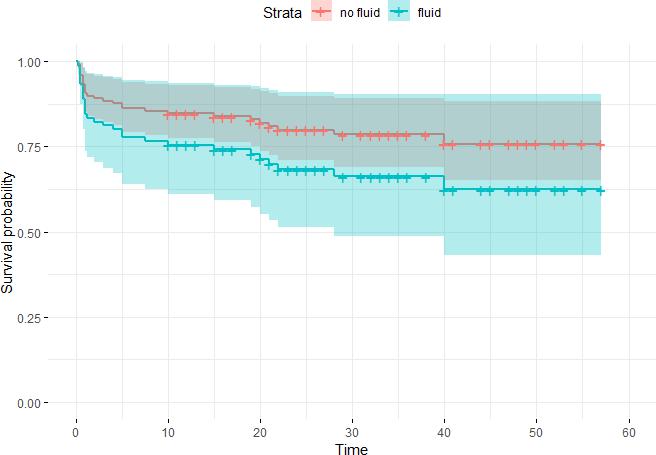
The survival curve of patients with heart disease was drawn only considering whether there waspericardial e”usion or not. As can be seen from the picture, the survival rate of heart patients withpericardial e”usion is lower than that of heart patients with pericardial e”usion over time.algorithm competition website代写
fit1 <- survfit(Surv(survival,alive)~factor(pericardialeffusion),data=echocardiogram) plot(fit1,mark=19,lwd=2,col=c(4,2), ylab="Survival Proportion", xlab="Months") legend(10,0.4,c("no fluid","fluid"),fill=c(4,2))
Cox PH regression
Now we’re going to describe how some of these factors come together to influence survival.To answerthis question, we will perform a multivariate Cox regression analysis. In multivariate Cox analysis, age andwallmotion index were significantly correlated (p<0.05).Pericardial e”usion was not significant (P = 0.20,which was larger than 0.05).Similarly, fractional shortening, epss, and LVDD have P values greater than 0.05, indicating that they contributed less to the di”erence in survival time.
The age p value was 0.000384,the risk ratio HR = exp (coef) =1.08116, and the 95% confidence interval (1.0355824, 1.129), indicating astrong relationship between the age of patients and the risk of death.The pericardial e”usion p value was0.204897, the risk ratio HR = exp (coef) =1.6994, and the 95% confidence interval was (0.7486333, 3.857),indicating that there was also a strong relationship between patient pericardial e”usion and the reducedrisk of death, but the fluctuation range was large.The risk ratio of covariates can be explained as themultiplier e”ect on risk.For example, fluid (pericardial e”usion= 1) that remains the same for other covariables increases the risk to 1.6994 times, that is, a 70 percent increase.We conclude that fluid patients are more likely to die.
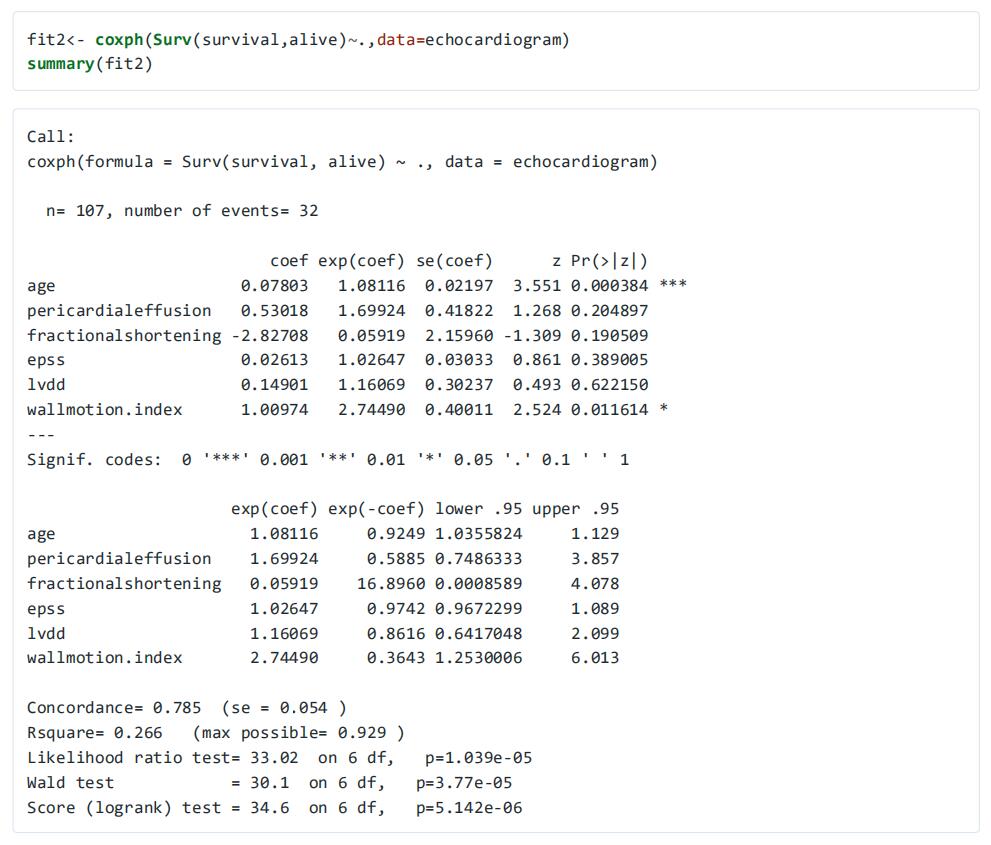
As can be seen from the figure below, the survival curve of heart patients with pericardial e”usion is lower than that of heart patients without pericardial e”usion, which indicates that heart patients with pericardiale”usion are more likely to die. The confidence interval of pericardial e”usion survival curve is very large, covering the confidence interval of non-e”usion survival curve, which indicates that the reliability of the results has some problems.
df<-with(echocardiogram,data.frame(pericardialeffusion=c(0,1),age=rep(mean(age),2), fractionalshortening=rep(mean(fractionalshortening,na.rm=TRUE),2), epss=rep(mean(epss,na.rm=TRUE),2), lvdd=rep(mean(lvdd,na.rm=TRUE),2), wallmotion.index=rep(mean(wallmotion.index,na.rm=TRUE),2))) curvesfit<-survfit(fit2,newdata=df) ggsurvplot(curvesfit,data=df,conf.int=TRUE,legend.labs=c("no fluid","fluid"), ggtheme=theme_minimal())
Model Fitting, using AIC to pick the right set of covariates
We use stepwise regression to optimize our model variables. After stepwise regression, we retained threevariables: epss, wallmotion index and age.Compared with the unoptimized model, the P values ofLikelihood ratio test, Wald test and Score (logrank) test are all reduced by an order of magnitude. Afteroptimization, the P values of the three overall tests of the model are far less than 0.05, which indicates that the model is significant on the whole. The P values of all three variables were less than 0.05,indicating that three variables were significantly correlated with survival time.algorithm competition website代写
fit3<-step(fit2)
Start: AIC=261.56
Surv(survival, alive) ~ age + pericardialeffusion + fractionalshortening +
epss + lvdd + wallmotion.index
Df AIC
– lvdd 1 259.81
– epss 1 260.29
– pericardialeffusion 1 261.06
– fractionalshortening 1 261.37algorithm competition website代写
<none> 261.56
– wallmotion.index 1 265.36
– age 1 271.71
Step: AIC=259.81
Surv(survival, alive) ~ age + pericardialeffusion + fractionalshortening +
epss + wallmotion.index
Df AIC
– pericardialeffusion 1 259.52
<none> 259.81
– fractionalshortening 1 259.94
– epss 1 259.98
– wallmotion.index 1 263.62
– age 1 270.54
Step: AIC=259.52
Surv(survival, alive) ~ age + fractionalshortening + epss + wallmotion.index
Df AIC
– fractionalshortening 1 258.96algorithm competition website代写
<none> 259.52
– epss 1 260.27
– wallmotion.index 1 263.86
– age 1 270.43
Step: AIC=258.96
Surv(survival, alive) ~ age + epss + wallmotion.index
Df AIC
<none> 258.96
– epss 1 261.05
– wallmotion.index 1 264.97
– age 1 270.83
summary(fit3)
Call:
coxph(formula = Surv(survival, alive) ~ age + epss + wallmotion.index,algorithm competition website代写
data = echocardiogram)
n= 107, number of events= 32
coef exp(coef) se(coef) z Pr(>|z|)
age 0.08139 1.08479 0.02154 3.778 0.000158 ***
epss 0.04566 1.04672 0.02165 2.109 0.034907 *
wallmotion.index 1.18291 3.26384 0.39005 3.033 0.002424 **
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1algorithm competition website代写
exp(coef) exp(-coef) lower .95 upper .95
age 1.085 0.9218 1.040 1.132
epss 1.047 0.9554 1.003 1.092
wallmotion.index 3.264 0.3064 1.520 7.010algorithm competition website代写
Concordance= 0.766 (se = 0.054 )
Rsquare= 0.242 (max possible= 0.929 )
Likelihood ratio test= 29.62 on 3 df, p=1.657e-06
Wald test = 28.7 on 3 df, p=2.587e-06
Score (logrank) test = 32.16 on 3 df, p=4.84e-07
Residual analysis algorithm competition website代写
COX regression assumes that Hazard Ratio (HR) does not change over time, that is, it satisfies theproportional risk assumption (PH assumption). Normally, Schoenfeld residuals should be independent oftime. If the residuals have a tendency to correlate with time, they will become evidence of violation of thePH hypothesis. From the following results, we can see that the P values of the three variables are greater than 0.05, indicating that each variable satisfies the PH test, while the overall P value of the model is 0.678, and the overall model satisfies the PH test.
cox.zph(fit3)
rho chisq p
age -0.162 0.741 0.389
epss 0.148 0.560 0.454
wallmotion.index -0.154 0.731 0.392 algorithm competition website代写
GLOBAL NA 1.518 0.678
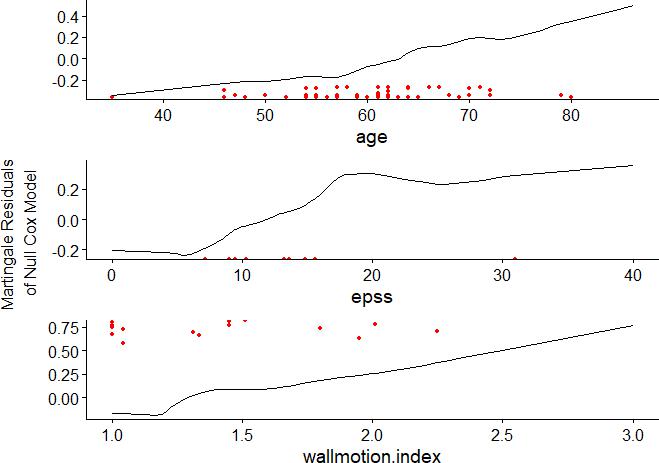
In general, we assume a linear relationship between covariates and-log(s(t)). Nonlinear diagnosis of model covariates can be achieved by drawing Martingale residual diagram. Nonlinear diagnosis is generally aimed at continuous variables in the model. As shown in the figure below, although the variables have a local non-linear trend, the overall trend is linear.
ggcoxfunctional(fit3,data = echocardiogram)
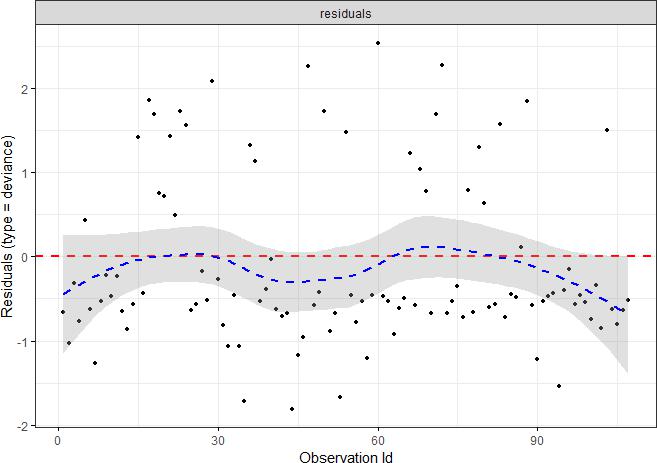
The residual values are uniformly distributed around 0, indicating that the model conditions are satisfied.
ggcoxdiagnostics(fit3,type = "deviance", linear.predictions = FALSE,ggtheme = theme_bw())
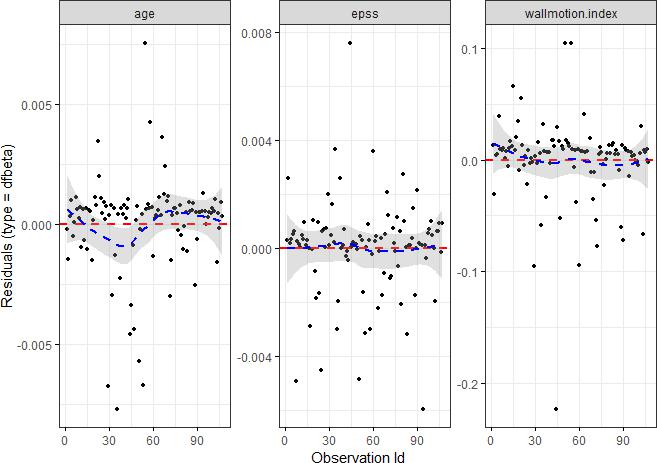
ggcoxdiagnostics(fit3,type = "dfbeta", linear.predictions = FALSE,ggtheme = theme_bw())
Extension
Heart disease patients are always concerned about how long they can survive. It is di cult to predict thesurvival time of patients accurately. We can reduce the di culty of judging whether a patient can survivefor more than a year. According to survival and survival variables, we can judge whether patients survive for more than one year. I can derive a new binary variable, aliveat1. 0 refers to patients who died withinone year or followed up for less than one year. 1 represents that the patient has survived for more thanone year. We can predict whether a patient will survive for more than a year based on the variablesavailable. Decision trees or random forests are my priority models. However, there may still be a problem. There are only 122 samples in the data set, which is a big challenge to the accuracy of the model.

其他代写:考试助攻 计算机代写 java代写 algorithm代写 assembly代写 function代写paper代写 金融经济统计代写 web代写 数学代写 编程代写 report代写 数学代写 finance代写 algorithm代写 matlab代写