MACM 201 – D100 AND D200 ASSIGNMENT #4
算法作业代写 Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page.
Instructions
Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page. If you use paper make a photo of each page and upload your solutions to crowdmark. If you use a tablet, export your assignment to .pdf and upload the .pdf to crowdmark.
Textbook Reading
- Sections: 10.2, 10.3
- DivAndConq.pdf notes (under Lecture Notes on Canvas)
Defifinitions, Concepts & Keywords
- Solve fifirst order non-homogenous recurrences.
- Solve some second order non-homogenous recurrences.
- Understand the Mergesort algorithm.
- Solve recurrences arising from divide-and-conquer algorithms.
Exercises 算法作业代写
A.Textbook Questions
Section 10.2 Exercise 24.
Section 10.3 Exercises 1(b+d), 8.
B.Questions
1.Below is C code and Python code for an algorithm.
C code:
1: void foo( int n, int A, int B, int C ) {
2: if( n==1 ) {
3: printf(“%d to %d\n”,A,B);
4: return;
5: }
6: foo( n-1, A, C, B );
7: printf(“%d to %d\n”,A,B);
8: foo( n-1, B, C, A );
9: }
Python code:
1: def foo(n , A, B, C):
2: if n==1:
3: print A, “to”, B
4: return
5:
6: foo(n-1, A, C, B)
7: print A, “to”, B
8: foo(n-1, B, C, A)
Let Hn be the number of times the printing function is executed. Assume n ≥ 1. Give a recur-rence equation and an initial value for Hn and solve it. Note, you do not need to know what the code is doing to answer this question.

2.John takes out a bank loan for $20,000 to buy a car. If the bank charges interest at 10% per year, and John has to pay back the loan over 5 years, how much does he have to pay every year? 算法作业代写
Use a recurrence. See example 10.29.
3.Consider the complete bipartite graph Kn,n with 2n vertices. Let kn be the number of edges in Kn,n. Draw K1,1, K2,2 and K3,3 and determine k1, k2, k3. Give a recurrence relation for kn and solve it using an initial value.
4.Calculate a formula for ![]()
5.Solve the recurrence an = 2an-1+ 4n-1 with a1 = 3.
6.Consider the recurrence an − 3an-1 + 2an-2 = n.
(a) Find the general solution to the associated homogenous recurrence.
(b) Find a particular solution.
(c) Find the solution for a0 = a1 = 1.
7.Consider the recurrence an − an-1 − 6an-2 = 5 · 3 n.
(a) Find the general solution to the associated homogenous recurrence.
(b) Find a particular solution.
(c) Find the solution for a0 = 7 and a1 = 5.
8.The recurrence for number of comparisons that the Mergesort algorithm does, assuming n = 2k ,is C(n) ≤ 2 C(n/2) + n − 1 and C(1) = 0. If the input array A is already sorted, give a recurrence for the number of comparisons Mergesort does and solve it. Hint: how many comparisons does the merging algorithm do?
9.Consider the recurrence T(n) = aT(n/b) + h(n) for h(n) = An + B with initial value T(1) = C where a, b are positive integers with b ≥ 2 and A, B, C are real numbers with A ≥ 0 and C ≥ 0.
Using the method in the proof of Theorem 10.1 solve for T(n). Simplify the formula for the case a = 1 and for the case a = b, b > 1.
10.Consider the polynomials f(x) = ![]() and g(x) =
and g(x) = ![]() both of degree n − 1. In 1960 Karatsuba gave a new algorithm to multiply f × g that does Tn arithmetic operations where Tn = 3Tn/2+ n/2 for n ≥ 2 and T1 = 1. Assume n = 2k for some integer k ≥ 0. Solve the recurrence for Tn and then check that your solution satisfifies the recurrence. You should get an answer of the form Tn = anlog2 3 + bn where a and b are constants.
both of degree n − 1. In 1960 Karatsuba gave a new algorithm to multiply f × g that does Tn arithmetic operations where Tn = 3Tn/2+ n/2 for n ≥ 2 and T1 = 1. Assume n = 2k for some integer k ≥ 0. Solve the recurrence for Tn and then check that your solution satisfifies the recurrence. You should get an answer of the form Tn = anlog2 3 + bn where a and b are constants.
Note, if you look up the Wikipedia page on Karatsuba’s algorithm, you will see that Karatsuba fifirst devised his the algorithm to multiply two n digit integers. The same algorithm works multiplying two polynomials of degree n − 1. The recurrence is simpler in the polynomial case.
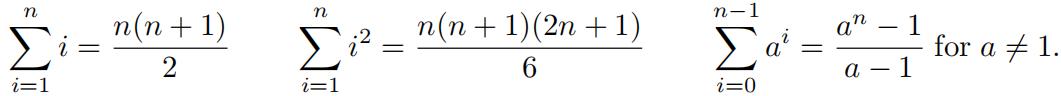
Table 1: Some useful sums

更多代写:统计代考 gre网考作弊被抓 加拿大数学作业代写价格 留学生essay论文范文代写 mla格式写作 加拿大统计代写价格
