CS 2100: Discrete Structures
Quiz 3
1.(15 points) 离散结构quiz代考
Let p0, p1,…,pnbe boolean variables. Define
ak = (pk + (ak−1)), where a0 = p0.
Prove the following boolean-algebra identity using proof by induction and the rules of boolean algebra (given below).
p0 · an = p0, for all n ≥ 1.
Equivalently this can be written out as:
p0 · (pn + (pn−1 + ··· + (p2 + (p1 + p0))···)) = p0, for all n ≥ 1.
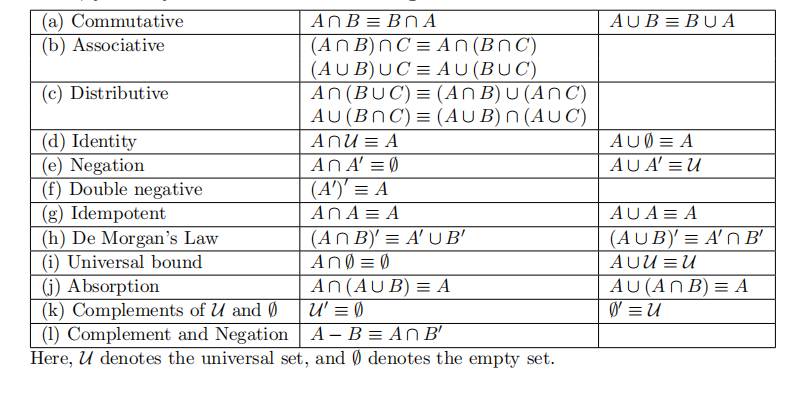
| (a) Commutative | p · q ≡ q · p | p + q ≡ q + p |
| (b) Associative | (p · q) · r ≡ p · (q · r) | (p + q) + r ≡ p + (q + r) |
| (c) Distributive | p · (q + r) ≡ (p · q)+(p · r) | p + (q · r) ≡ (p + q) · (p + r) |
| (d) Identity | p · 1 ≡ p | p + 0 ≡ p |
| (e) Negation | p · p’ ≡ 0 | p + p’ ≡ 1 |
| (f) Double negative | (p’)’ ≡ p | p + p ≡ p |
| (g) Idempotent | p · p ≡ p | |
| (h) De Morgan’s Law | (p · q)’ ≡ p’ + q’ | (p + q)’ ≡ p’ · q’ |
| (i) Universal bound | p · 0 ≡ 0 | p + 1 ≡ 1 |
| (j) Absorption | p · (p + q) ≡ p | p + (p · q) ≡ p |
| (k) Negations of 1 and 0 | 1’ ≡ 0 | 0’ ≡ 1 |
Please fill in the missing steps in the following inductive proof. Please cite which rule you are using (a letter is fine). Do not skip or merge steps.
Induction statement: P(n)=“p0 · an = p0, for all n ≥ 1”
Base case: Show P(1)
Your work here. . .
Induction hypothesis: Assume P(n − 1).
Induction step: Show P(n) assuming P(n − 1).
Your work here. . .
2.(10 points) 离散结构quiz代考
Let A and B be sets. We define the symmetric difference of two sets as:
A △ B ≡ (A − B) ∪ (B − A).
Another possible definition of the symmetric difference is:
A △ B ≡ (A ∪ B) − (A ∩ B).
Using Venn diagrams, show these two definitions are equivalent, that is, show
(A − B) ∪ (B − A) ≡ (A ∪ B) − (A ∩ B).
Note: You must clearly show your steps and identify the sets. You will receive no credit for simply writing the answer.
3.(10 points)
Suppose A = {∅, 2, {2}, {2, 3}, 4}. Indicate whether each of the following statements is true or false. No explanation needed.
(a) (T) (F) 2 ∈ A
(b) (T) (F) {2, 3} ⊆ A
(c) (T) (F) ∅ 2 A
(d) (T) (F) {∅} ⊆ A
(e) (T) (F) |A| = 5 (or n(A) = 5)
(f) (T) (F) ∅ 2 P(A)
(g) (T) (F) ∅ ⊆ P(A)
(h) (T) (F) {{2, 3}} ∈ P(A)
(i) (T) (F) {{2, 4}} ⊆ P(A)
(j) (T) (F) (2, {4}) ∈ A × A
4.(20 points) 离散结构quiz代考
Let A = {10k +3: k ∈ Z}, B = {10l +8: l ∈ Z}, and C = {5m +3: m ∈ Z}. Show that {A, B} is a partition of C.
Hint: your proof should contain the following:
(a) prove that A and B are not empty.
(b) prove that A and B are disjoint, meaning they have no common elements. (Think about the division theorem.)
(c) prove completeness, that is, A ∪ B = C, i.e., A ∪ B ⊆ C and C ⊆ A ∪ B.
5.(15 points)
Using the methods of proof by contrapositive and element-wise proof, show that if A ∩ B ⊆C AND x ∈ B complete the proof by using , then x ∉ A − C. Begin by stating the contrapositive, then proof by cases.
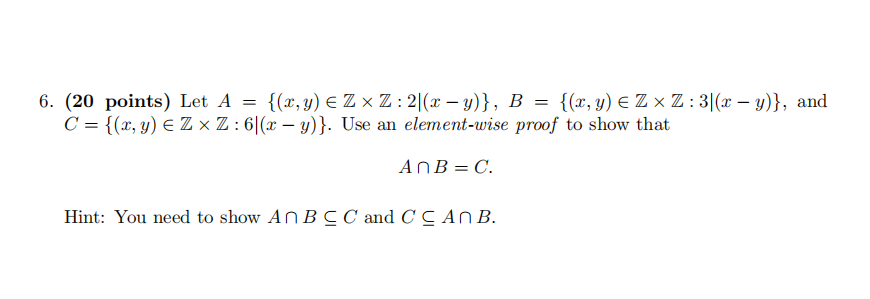
7.(10 points) 离散结构quiz代考
The symmetric difference operation, A △B, is defined as
A △ B ≡ (A ∪ B) − (A ∩ B).
Or, equivalently,
A 4 △ ≡ (A − B) ∪ (B − A).
By quoting the properties from Theorem 6 (given below) prove the following:
(A ∪ B) − (A ∩ B) ≡ (A − B) ∪ (B − A).
Hint: Begin by applying “Complement and Negation” to both sides, then use the properties to show the left-hand side equals the right-hand side. Please cite which rule you are using (a letter is fine). Do not skip or merge steps. If you get stuck, you may have better luck working from the other side.

更多代写:cs澳大利亚网课代考推荐 雅思代考价格 英国医学Medicine代写 北美essay作业代写 澳大利亚经济学代考 离散结构练习题代写
