CS 2100: Discrete Structures
Homework 3
离散结构课业代写 1.Exercise 2.a on page 193.Let A = {x ∈ N: x = 4k for some k ∈ N}, B = {y ∈ Z+ : 2y is a perfect squareu}, and C = {z ∈ Z : z2 ﹤ 1, 000}.
1.Exercise 2.a on page 193.
Let A = {x ∈ N: x = 4k for some k ∈ N}, B = {y ∈ Z+ : 2y is a perfect squareu}, and C = {z ∈ Z : z2 ﹤ 1, 000}. List five elements in the following set: A ∪(B ∩ C).
2.Exercise 16.b on page 195. 离散结构课业代写
Use Venn diagrams to verify the following property of our set operations:
One of DeMorgan’s laws:
(A ∪ B)’ = A’ ∩ B’
3.Exercise 18.b and 18.e on page 195.
Given A = {2x : x ∈ Z} and B = {3y : y ∈ Z}, describe each of the following using the simplest set-builder notation possible:
(a) A – B
(b) Z – A
4.Exercise 1.b on page 209. 离散结构课业代写
Given the universal set U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and set A = {2, 4}, B = {1, 2, 8}, and C = {1, 2, 5, 6, 10}, find the following:
(A × B) ﹣ (A × A)
5.Exercise 9 on page 209.
Let A = {2k : k ∈ Z}, B = {4k + 1 : k P Z}, and C = {4k + 3 : k ∈ Z}. Explain why {A, B, C} is a partition of Z.
6.Exercise 2.e on page 219. 离散结构课业代写
Prove the following statement about specific sets:
({2n + 1 : n ∈ Z} ∩ {5m + 4 : m ∈ Z}) ⊆ {10k + 9 : k ∈ Z}
7.Exercise 11.d on page 220.
Give an element-wise proof for the following:
If A ∪ B = B and B ∪ C = C , then A ∪ C = C.
8.Exercise 13.c on page 220. 离散结构课业代写
Give an element-wise proof for the following:
If A ⊆ B , then A ∪ (B – A) = B.
9.Exercise 14.e and 15.e on page 220.
Consider the following equation:
(A ∪ B) ∩ (A’ X C)’ = A ∪ (B ∩ C’)
(a) Prove the equation by quoting the appropriate parts of Theorem 6.
(b) Form the dual of the equation.
10.Exercise 22.a on page 221. 离散结构课业代写
Prove the following statement:
(A ∩ B) × C = (A × C) ∩ (B × C)
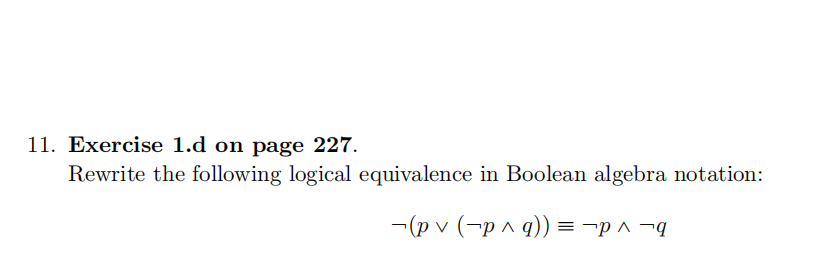

更多代写:Code代码代做 sat考试作弊 英国Chemistry网课代做 College level Essay代写 CSR代写范文 国外简历代写
