CS 2100: Discrete Structures
Practice Final

2.
This is a question on expected values of random variables. Your company plans to invest in a particular project. There is a 40% chance that you will lose $2000, a 40% chance that you will break even (i.e. you will not loose or gain any money), and a 20% chance that you will make $5000. Based solely on this information, should you proceed with the project?
Hint: Let X be the value of the amount of money you make (positive values) or loose (negative values); compute the expected value of the project.
3. 离散结构练习代考
(a) A card player is dealt a poker hand (5 cards) from an ordinary playing deck with 52 cards. Find the number of ways the player could be dealt a spade flush (that is, 5 spades).
(b) Solve problem (a) if the player is dealt an ace-high spade flush (that is, five spades with the ace).
4.
What is the probability of getting at least two 3’s on five tosses of a fair six-sided die?
5. 离散结构练习代考
30 children from the fourth grade, 15 boys and 15 girls, are standing in line. Assume that all the possible ways the children might line up are equally likely.
(a) Assuming no two of the children have the same name, what is the probability the children appear in line in alphabetical order by name?
Hint: there is only one alphabetical order among all possible lines.
(b) What is the probability all the girls precede the boys?
(c) What is the probability that they alternate by gender in line?
6. 离散结构练习代考
(a) Determine whether or not each of the following is equal to A, the empty set ∅, or the universal set U (A’means the complement of A):
- A ∩ U = __________
- A − A = __________
- A − U = __________
- A − ∅ = __________
- A − A’ = __________
- (A’)’= __________
(b) Suppose A and B are sets. P(A) means the power set of A. Use direct proof to show the following: if P(A) ⊆ P(B), then A ⊆ B.
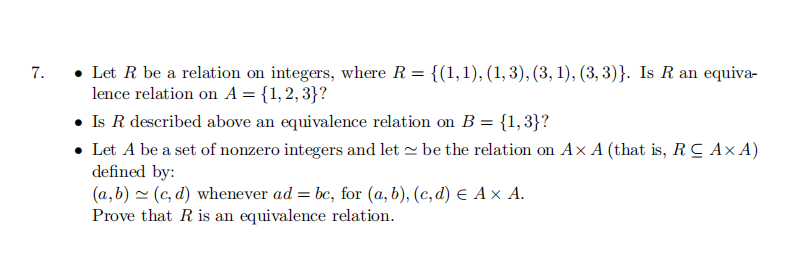
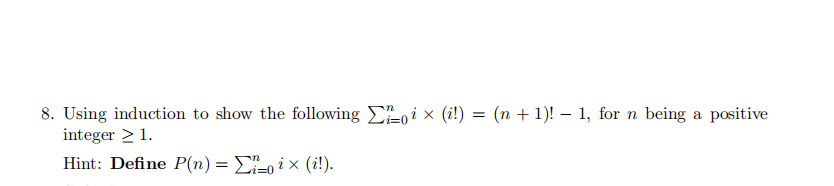
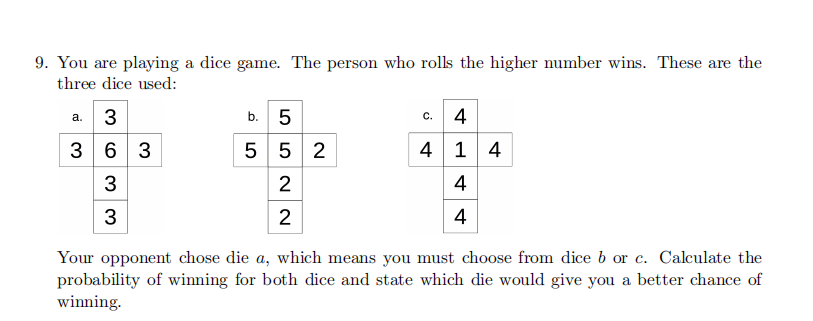
10.
(a) Describe the arrow diagram of a relation R from a finite set A to a finite set B.
Illustrate using the relation R from set A = {1, 2, 3, 4} to set B = {x, y, z} defined by R = {(1, y),(1, z),(3, y),(4, x),(4, z)}.
(b) Draw the arrow diagram of the inverse relation R−1 .
11. 离散结构练习代考
A plane graph is a planar embedding of a planar graph.
Prove that if G is a plane graph with more than two vertices, then G has a vertex of degree at most 5.
12.
Vertex coloring is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color.
Show that any plane graph G can be 6-colored. That is, one can generate a vertex coloring of the graph G using 6 different colors.
Hint: make sure of the result in the previous problem, that is, any plane graph with more than two vertices has a vertex of degree at most 5.

更多代写:cs澳大利亚网课代上多少钱 考试助攻 英国理工代写 理工科论文代写 理工科Assignment代写 离散结构quiz代写
