离散数学和概率论代写 CS 70代写

CS 70 Discrete Mathematics and Probability Theory

Midterm

离散数学和概率论代写 Remote Proctoring Instructions. On questions 1-11: You need only give the answers on the “Midterm (Short Answers)” gradescope assignment

Remote Proctoring Instructions.

• On questions 1-11: You need only give the answers on the “Midterm (Short Answers)” gradescope assignment within the 2 hour time period of the exam. (No justification is required.)
• On questions 12-14, the answers will be written on separate sheets of paper for each part. You will need to scan seven sheets of paper to a separate gradescope assignment called Midterm (PDF and long answers.). Each part can only use one page; the solutions use much less, so one page per part is a hard limit.
• Be sure to download the PDF from the Midterm (PDF and long answers) gradescope assignment.
• Both gradescope assignments will be available at 8:00 PM and the PDF for the entire exam including short answers will be available on the “Midterm(PDF and long answers)” assignment.
• There will be no clarifications. If a problem part has an error, we will remove it from the midterm.
• You have 120 minutes which includes the time to fill out the answers in the Midterm(Short Answers) gradescope assignment and then an extra twenty minutes to scan your paper solutions to the Midterm (PDF and long answers) assignment.

 

 Advice.   离散数学和概率论代写

• The questions vary in difficulty. In particular, some of the proof questions at the end are quite accessible, and even those are in not necessarily in order of difficulty. Also points (pts) are indicated in each problem heading in the pdf. So do really scan over the exam a bit.
• The question statement is your friend. Reading it carefully is a tool to get you to your “rational place”.
• You may consult only one sheet of notes on both sides. Apart from that, you may not look at books, notes, etc. Calculators, phones, computers, and other electronic devices are NOT permitted.
• You may, without proof, use theorems and lemmas that were proven in the notes and/or in lecture, unless otherwise stated. That is, if we ask you to prove a statement, prove it from basic definitions, e.g., “d|x means x = i(d) for some integer i” is a definition.

 

 

2.   离散数学和概率论代写

Warmup, Propositions, Proofs: 2 points/part unless otherwise stated.

1. ¬(P ⇒ Q) ≡ (P∧ ¬Q)

❤True

❤False

2. ∀x ∈ S,(Q(x)∨P(x)) ≡ (∀x ∈ S,Q(x))∨(∀x ∈ S,P(x))

❤True

❤False

For the following two parts, assume Q(x, y) and P(x) are predicates over the domain of x, y.

3. (∃x,∀y,Q(x, y)∧P(x)) ⇒ ∃x,P(x)

❤True

❤False

4. (∃x,∀y,Q(x, y)∨P(x)) ⇒ ∃x,P(x)

❤True

❤False

5. P(0)∧(∀n ∈ N P(n) ⇒ P(n+1)) ⇒ ¬(∃n ∈ N¬P(n))

❤True

❤False

6. More Cards to Flip? (4 points.) Your friend states that “All plants that are shipped to a Californian address must have originated in California”. Staying indoors with windows closed all day, you are suddenly intrigued by this rule.

Which of the following would you do to test (falsify) your friend’s statement?

(a) Find the destination of Megan’s English Ivy plant, being shipped from Oregon

(b) Find the destination of Tyler’s Rubber Tree plant, being shipped from California

(c) Find the origin of Albert’s Aloe Vera plant, who received it in California

(d) Find the origin of Lili’s Bamboo Palm plant, who received it in Seattle

(Answer may include more than one.)

7. If n and m have the same prime factorizations, then they are the same number.

❤True

❤False

8. If xy = n and uv = n, with x < y and u < v, then x = u and y = v.

❤True

❤False

9. If d|x and d|x+2y then d|y.

❤True

❤False

 

3.Stable Matchings. 2 points/part.    离散数学和概率论代写

Stable Matching: In the following consider a stable matching instance with n candidates and n jobs each with complete preference lists.

1. The only stable pairing in any instance is produced by the job propose and candidate reject algorithm.

❤True

❤False

2. Any job has a unique pessimal candidate.

❤True

❤False

3. If a candidate rejects a job in the job propose and reject algorithm, there is no stable pairing where that candidate and job are paired.

❤True

❤False

4. Consider any stable matching instance, and a run of the job propose and candidate reject algorithm, where exactly one candidate, c, misbehaves. In particular, rejects some job j falsely (that is rejects a job j for a job j 0 that c prefers less). In this scenario, c is the only candidate that can be in a rogue couple in the final pairing.

❤True

❤False

5. There is no stable pairing where every job is paired with its least preferred candidate.

❤True

❤False

 

4.Graphs. 2 points/part unless otherwise indicated.    离散数学和概率论代写

All graphs are simple in this problem, unless otherwise stated.

1. Any tree is bipartite.

❤True

❤False

2. Any graph G = (V,E) with |E| ≥ |V| is connected.

❤True

❤False

3. Every graph that is vertex-colorable with d colors has max degree d −1.

❤True

❤False

4. Any cycle can be edge colored with 2 colors. (Recall edge coloring is a coloring of edges so that any pair of edges incident to the same vertex have different colors.)

❤True

❤False

5. (4 points) For a graph G, consider a walk which contains any edge at most once and contains all the edges incident to each of its two distinct endpoints, u and v. Recall that a walk is a sequence of edges where successive edges share an endpoint, thus this walk does not reuse edges but does use all the edges incident to u and v.

If the endpoints, u and v, are different:

(A) Their degrees must be the same.

(B) Each must have even degree.

(C) Each must have odd degree.

(D) The sum of the degrees of the two vertices is even.

Answer all that are true.

6. Any graph with v vertices and v−k edges for k ≥ 0 and has exactly one cycle has connected components.
7. There is a simple graph with average degree of exactly 2 that has no cycles. (Recall that simple means there is at most one edge between any pair of nodes.)

❤True

❤False

8. There is a directed graph, where the sum of the outdegrees over all vertices is greater than the sum of indegrees over all vertices.

❤True

❤False

 

5.Planar graphs. 3 points/part.    离散数学和概率论代写

Consider a connected planar graph with v ≥ 3 vertices, and where every cycle has length at least 6.

1. Give an upper bound on the number of edges, e in terms of the number of vertices, v. (Recall, for example, that any for any planar graph e ≤ 3v−6. Your upper bound should be as tight as possible.)
2. How many colors is always sufficient to vertex colored such a graph?

 

6.Modular Arithmetic:short answer. 2 points per part.

1. What is 2¹¹(mod 11)?
2. What is 2²⁵(mod 33)?
3. ab ≡ 0 (mod N) implies that a ≡ 0 (mod N) or b ≡ 0 (mod N).

❤True

❤False

4. For primes p and q, find all values of x ∈ {1,…, pq−1}, where x|(a^{k(p−1)(q−1)+1}−a)?
5. If a ≠1 (mod N) and a^k(N−1)≠ 1 (mod N) then N is not prime.

❤True

❤False

6. How many solutions are there to ax = b (mod n), if gcd(a,n) = d and gcd(b,n) = d?
7. Find x ∈ {0,…, pq−1} where x = a (mod p) and x = 0 (mod q) where p and q are prime? (Answer expression that may involve a, p, q, (mod q), (mod p) and inverses, e.g., (q⁻¹(mod p)).)
8. For x, y ∈ Z for x ≠y, what is the minimum value of |x − y| if x = y = a (mod p) and x = y = b (mod q) for primes p and q?

 

7.Another Proof. 3 points/part.    离散数学和概率论代写

Another proof for RSA can be done as follows.

1. Let S be the set of numbers {0,…, pq−1} relatively prime to pq. What is |S|? (Recall, a and b are relatively prime if gcd(a,b) = 1.)
2. For a with gcd(a, pq) = 1, and T = {ax (mod pq)|x ∈ S}, what is the size of T?
3. What is a^|T|(mod pq)?

 

8.Polynomials: Background. 2 points/part.

When we count roots, we mean with multiplicity unless otherwise stated. That is, Q(x) = (x−2)² has two roots. Polynomials are over a field unless otherwise specified.

1. If two polynomials of degree 7 in share points then they must be the same (working (mod 17).)

(Answer is the smallest integer that makes the statement true.)

2. If a non-zero polynomial has d roots it must have at least degree_____.
3. How many roots does the polynomial, x²−2 (mod 5) have?
4. If a polynomial has d roots it’s degree is at most d.

❤True

❤ P False

5. Given a polynomial Q(x) = P(x)(x−2)(x−4), and d is the degree of Q(x), what is the degree of(x)?
6. Given a polynomial Q(x) = P(x)(x−2)(x−4), and if P(x) has r roots, what is the number of roots for Q(x)?

 

9.Polynomials: applications. 2 points/part.    离散数学和概率论代写

Recall for secret sharing and error tolerance to erasures and corruptions that one works over arithmetic modulo a prime p. In each of the following situations, how big should p be? (That is, fill in the blank for p ≥ _____.)

1. One wishes to share a secret with b-bits among n people where any k can reconstruct the secret.
2. One wishes to communicate a message of n packets with b bits each and wants to tolerate k erasures?
3. One wishes to communicate a message of n packets with b bits each and wants to tolerate k corruptions?

 

10.Counting: Basics. 2 points/part.

Let S = {1,…,n}.

(A) All subsets of S.

(B) The number of subsets of S of size k.

(C) The number of subsets of S of size n−k.

(D) The number of ways for k non-negative integers that add up to n.

(E) The number of ways for k positive integers that add up do n.

For each of the expressions, indicate the letter of the option above that it coresponds to.

 

 

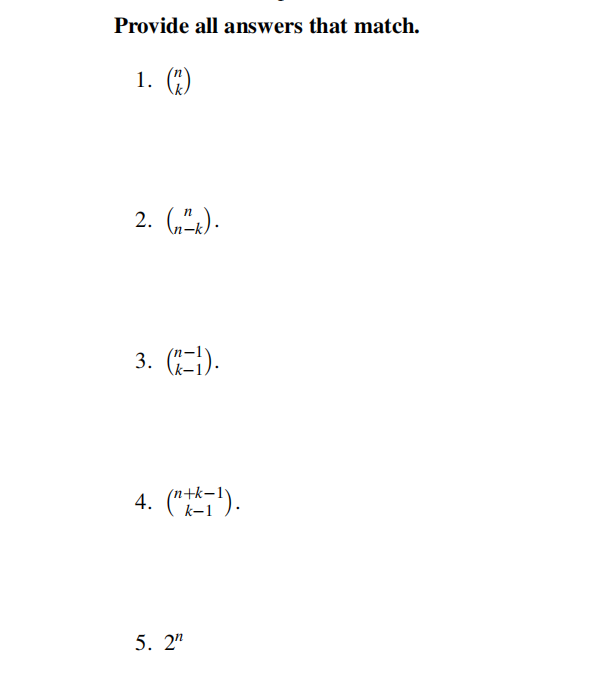
11.Counting and Polynomials. 2 points/part.

Counting and Polynomials. Assume all polynomials are over (mod p) where p is a prime and p > d.

Again, when we count roots, we mean with multiplicity unless otherwise stated. That is, Q(x) = (x−2)² has two roots.

1. What is the number of roots of a degree 1 polynomial (mod p)? (A degree one polynomial is ax+b, where a is non-zero.)
2. What is the number of degree d polynomials?
3. What is the number of exactly degree d polynomials with d distinct roots?
4. What is the number of exactly degree d polynomials with d roots (allowing for multiplicity)?

The Remainder of the Exam is written, and you should be scanning 7 pages for you answers.

 

12.Quick(ish) Proofs. 3pts/3pts/5pts.   离散数学和概率论代写

You must write your answer for each subproblem on a separate clearly labelled page.

1. Prove: If d|x and d|y+kx then d|y for any integer k.
2. Prove: If n²−6n+5 is even, then n is odd.
3. Prove by induction: For all positive natural numbers n ≥ 1 and that 3(7ⁿ) +2⁽⁵ⁿ⁻³⁾is divisible by 25.

(It may be useful to see that 2⁵ = 32 = 25+7 and that 2^a+b = 2^a2^b.)

 

13.Set Operations. 5 points.   

For a function g, define the image of a set X to be the set g(X) = {y | y = g(x) for some x ∈ X}.

Hint: For sets X and Y , X = Y if and only if X ⊆ Y and Y ⊆ X. To prove that X ⊆ Y , it is sufficient to show that (∀x) ((x ∈ X) ⇒ (x ∈ Y)).

Let X∆Y = (X −Y)∪(Y −X), where X −Y = {x|x ∈ Xandx ∉ Y}.

Prove g(X)∆g(Y) ⊂ g(X∆Y)

 

14.Edge Coloring when there is no Hotel California. 4 pts/4pts/5pts.   离散数学和概率论代写

Please write your answer for each part on a separate page for scanning.

1. Show that an even length cycle can be edge colored with 2 colors. (Recall edge coloring is a coloring of edges so that any pair of edges incident to the same vertex have different colors.)

Recall that a bipartite graph G = (U∪V,E) where E⊂U ×V, i.e., there are two sets U and V and every edge consists of a vertex from U and a vertex from V. It is useful to recall (without proof) that any cycle in a bipartite graph has even length.

For the following two parts, we consider a bipartite graph, G = (U∪V,E) where every vertex has degree d = 2^k .

2. Show that |U| = |V|.
3. Show that the graph can be edge colored with d = 2^kcolors. (Hint: a previous part has something to do with k = 1.)

 

 

更多代写：cs exam网课代考  lsat代考  英国fin网课代写   lab essay代写  Methodology写作  数学半群代考

合作平台：essay代写 论文代写 写手招聘 英国留学生代写