CS 70 Discrete Mathematics and Probability Theory
离散数学代写 You can (if you choose) use latex. It is fairly easy and satisfying. Surround an expression by “$$ … $$” on gradescope and you will be in latex.
Some Latex Commands for Gradescope.
You can (if you choose) use latex. It is fairly easy and satisfying. Surround an expression by “$$ … $$” on gradescope and you will be in latex. Examples: “$$ A+B*D $$” will give: A+B∗D. There are useful commands:

1.Long Ago.
1.A∨ ¬(B∧C) ≡ A∨ (¬B∨ ¬C)
True
False
2.¬∀x,∃y,Q(x, y) ≡ ∃x,∃y,¬Q(x, y)
True
False
3.P ⇒ Q is logically equivalent to ¬Q∨P.
True
False
4.Consider a stable matching instance where S is the job optimal stable pairing. Consider a run of the job-propose matching algorithm, where one candidate c rejects a job j that they should not have in one step. That is, c recieves an offer from j and j‘ and chooses j‘ instead of j, when j was ahead of j‘ in their preference list.
Let P be the resulting pairing.
(a) For every instance, job j cannot do better in P than in S. (Better means get a partner who they prefer more.)
True
False
(b) Every candidate other than c does as well or better in P than in S.
True
False
(c) Every job other than j does as well or better in P than in S.
True
False
2. Graphs 离散数学代写
1.Consider a graph on n vertices with exactly one cycle and m edges. What is the number of connected components? (Hint: m ≤ n.)
2.For a tree on n vertices, what is the expected number of connected components if each edge is deleted with probability 1/3?
3.If we delete every edge with probability 1/2 from an Eulerian graph on n vertices, what is the expected number of odd degree vertices in the remaining graph?
4.Every simple cycle is 2-colorable.
True
False
3.Mostly Modular. 离散数学代写
1.∀ nonzero x, y ∈ N gcd(x, y mod x) = gcd(x, y).
True
False
2.∀ nonzero x, y ∈ N, gcd(x, x mod y) = gcd(x, y).
True
False
3.Give an example of positive integers for a and n where
(1 · 2···(n−1))an-1 ≠ (1 · 2···(n−1)) (mod n).
a:______________
n:______________
4.Let S = {x : x ∈ {1,…,34} and gcd(x,35) = 1}?
(a) What is the size of the set S?
(b) What is a|S|+1 (mod 35) for a ∈ S?
(c)What is a|S|+1 (mod 35) for a 6∈ S?
5.What is 18-1 (mod 13)?
6.If x = 1 (mod 13) and x = 0 (mod 18) then what is x (mod 234)? (Note: 234 = 18×13)
7.For primes, p and q, where e = d-1 (mod (p−1)(q−1))?
(a) What is aed (mod q)? (Answer cannot use e or d, but may use numbers, a,p or q.)
(b) Find an x ≤ pq, where p|(aed −x). (Answer is an expression that may use a, p, and q.)
4.Polynomials. 离散数学代写
1.Given a polynomial, x³ +a2x² +a1x+a0 modulo 7 with roots at 3, 1, and 6. What is a0? (Notice that the coeffificient of x³ is 1.)
2.Working (mod 5), fifind a polynomial modulo 5 of degree 2 that has roots at 0 and 3, and goes through point (2,3)
3.Consider that one encodes a message of n numbers (mod m), by forming a degree n−1 polynomial using the numbers as coeffificients, and sending 2n−1 points. If each point is erased with probability 1/2, what is the probability that the original message can be reconstructed? (Hint: each pattern of erasures is equally probable.)
5.Countability/Computability. 离散数学代写
1.For every pair of distinct rational numbers there is a rational number in between them.
True
False
2.The rational numbers are uncountable.
True
False
3.There is a program that takes a program P, an input x, and a number n and determines whether P run on input x ever writes to memory location n.
True
False
4.There is a program that takes a program P, an input x, and a number n and determines whether P run on input x ever writes to any memory location i ≥ n.
True
False
5.A program “knows” a real number if it takes an integer n and outputs the nth bit of the real number. (Note: positive values of n signify to the left of the decimal point, and negative ones to the right.)
(a)There is a program that knows π.
True
False
(b)For every real number x, there is a program that knows x.
True
False
6.A little counting.
1.What is the number of ways to have k strictly positive numbers that add up to n?
2.What is the number of ways to produce a sequence of numbers 0 < x1 < x2 < ··· < xk < n?
3.What is the number of ways to produce a sequence of numbers 0 ≤ x1 ≤ x2 ≤ ··· ≤ xk < n?
4.What is the number of poker hands that have at least 1 ace? (Recall that a poker hand is 5 cards from a 52 card deck.)
7.Probability. 离散数学代写
1.Consider rolling two six sided fair dice.
(a) What is the probability that exactly one die is 6?
(b) What is the probability that the sum of the two dice is 6?
(c) What is the probability that the sum is 6 given that at least one die is at least 3?
(d) The event of rolling a 6 on the fifirst die is independent of the event that the dice sum to 7.
True
False
(e) The event of rolling at least one 6 is independent of the event that the dice sum to 7.
True
False
2.Flip a coin until you repeat either heads or tails 2020 times. We will derive the probability that the fifirst coin is the same as the last coin in the entire sequence of flflips.
(a)If the process stops after 2020 tosses, what is the probability that the fifirst and last coin are the same?
(b)If the process stops after 2021 tosses, what it the probability that the fifirst and last coin are the same?
(c) What is the probability that the fifirst coin is the same as the last coin in the entire sequence of flflips?
3.Which of the following are always true.
(a)E[10X] = 10E[X]
True
False
(b)E[X² ] = E[X]²
True
False
(c)E[(X −Y)² ] = E[X² ] +E[Y²]−2E[X]E[Y]
True
False
(d)Var(X +Y) = Var(X) +Var(Y)
True
False
8.Marbles. 离散数学代写
Consider two bags of marbles, the “majority red” bag has 6 red marbles and 4 blue marbles, and the “majority blue” bag has 3 red marbles and 7 blue marble, and each bag is chosen with probability 1/2.
1.If you draw a blue marble where each marble in the bag is equally likely, what is the probability that the bag is the “majority blue” bag.
2.What is the probability that the next marble is blue?
9.Variance, covariance, tail bounds.
1.If E[X] = 4, and E[Y] = 5, and E[XY] = E[X]E[Y], what is cov(X,Y)?
2.A student earns one standard deviation above the mean on both exam 1 and exam 2. We defifine random variables X and Y as the score of a randomly chosen student on exam 1 and exam 2 respectively. If Var(X) = 1, Var(Y) = 1 and Cov(X,Y) = .5, how many standard deviations above the mean did the student get on the sum of her two scores? (Recall, Var(X +Y) = Var(X) +Var(Y) +2Cov(X,Y). )
3.For a random variable, X, where X ≥ −1, E[X] = 5, and E[X² ] = 26. Give an upper bound Pr[X ≥ 6]. (It should be tight with respect to the appropriate inequality.)
4.For a random variable, X, where E[X] = 5, and E[X² ] = 26, give an upper bound Pr[X ≥ 9]. (It should be tight with respect to the appropriate inequality.)
10.Markov Chain.
Consider the following Markov chain.
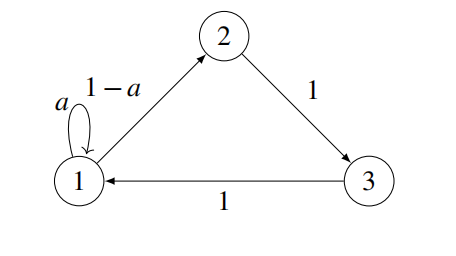
1.For what value of a does the chain have a unique invariant distribution but does not always converge to it.
2.For a = 1/2, what is the stationary distribution?
π(1):__________
π(2):__________
π(3):__________
11.Balls and Bins. 离散数学代写
Consider placing 5n balls into 3n bins uniformly at random. (Careful, the constants in front of the n’s are important.)
1.What is the expected number of empty bins?
2.What is the variance of the number of empty bins?
3.What is the expected number of non-empty bins?
4.What is the variance of the number of non-empty bins (in terms of the answer for part (1),(2) and/or (3).)
12.Sequential Dice.
Consider rolling a dice repeatedly and until one gets two 6’s in a row.
1.Draw a three state Markov chain where the states are labelled A,B, and C. Your chain should have a state C which is the “goal”; the previous two rolls were a 6. State A should indicate that one has not rolled any die or that the previous die is not 6.
2.What is the expected number of rolls to roll two 6’s in a row?
3.What is the probability of rolling two 6’s in a row prior to rolling a 5? (Hint: add a state to your previous Markov Chain and do a computation.)

其他代写:加拿大代写 作业代写 作业加急 英国代写 北美作业代写 homework代写 java代写 matlab代写 program代写 project代写 essay作业代写 finance代写 python代写 report代写 paper代写 assignment代写
