社会科学作业代写 business代写

Name:

Student ID:

社会科学作业代写 Consider the following population of ten representative children whose visual acuity we can measure. Visual acuity is the decimal version

Homework 2

Submit only answers when turning in your homework. Do not copy questions.

1.The American Academy of Ophthalmologynoted that observational studies (you don’t need to read that link) consistently find that playing outside appears to cause children to have better eyesight. We are interested in this hypothesis. [Total: 28 points]

	Potential Outcomes (POs): Visual Acuity
	If did play outside >10 hrs/week (PO if in Treatment)	If did not play outside >10 hrs/week (PO if in Control)	Individual Treatment Effect
Child 1	1.1	1.1
Child 2	0.1	0.6
Child 3	0.5	0.5
Child 4	0.9	0.9
Child 5	1.6	0.7
Child 6	2.0	2.0
Child 7	1.2	1.2
Child 8	0.7	0.7
Child 9	1.0	1.0
Child 10	1.1	1.1

Consider the following population of ten representative children whose visual acuity we can measure. (Visual acuity is the decimal version of the output of eye exams. For example, someone with 20/20 vision (considered “normal”) has acuity 1.0, while someone with 20/40 vision has acuity 0.5, which is more poor vision. Numbers greater than 1.0 are possible for people with better than “normal” visual acuity.) 社会科学作业代写

a.What do Child 2’s two potential outcomes mean in plain language? [2points]

b.Givethe individual true treatment effect (that is, the true “impact” or “causal effect” of playing outside) for each of the ten We are thinking of the “Treatment” as playing outside, so consider the Treatment Group to be the children who did play outside > 10 hrs / week. [2 points]

Notes:

Thisis only possible because we are working with hypothetical potential outcomes; we could never have this much information with real-world data.
For the sake of illustration, we are assuming a meaningful cutoff around 10 hours/week. All that matters is whether a child played more or less than this amount, making the treatment a yes/no variable. The notion of an average treatment effect generalizes to multiple treatments and to continuous treatments.

c.For these children, what is the true average treatment effect (ATE) of playing outside? (Please show your work.) [5points] 社会科学作业代写

d.Suppose we are able to do an experiment in which we can decide the amount of time that these children play outside (i.e., we can force them to play outside or not). We randomly assign the children to Treatment and Control group. Assume thatby chance (that is, suppose this is random) the odd-numbered children are assigned to Treatment (play outside) and the even-numbered children to Control (don’t play outside). What is the estimate of the ATE you would reach under that particular assignment? (Please show your work.) [5 points]

e.How different is the estimate from the truth you calculated in part (d)? Intuitively, why is there a difference? [5points]

f.Supposethat we decide it is too hard to control the behavior of the children, so we do an observational study Children 1-5 choose to play an average of more than 10 hours per week from age 3 to age 6, while Children 6-10 play less than 10 hours per week. If you were to naively try to estimate the impact of playing outside from this observational study, what impact would you estimate? That is, take the difference in the means of the observed outcomes for Children 1-5 and Children 6-10. (Please show your work.) [5 points]

g.Compare your answer in (f) to the true ATE from part (c). Intuitively, what other than random chance could cause this difference? [4points]

2.Retail Catalogues (from GG 9.4): [Total: 10points] 社会科学作业代写

Your company simultaneously runs two experiments measuring the impact of sending catalogues to frequent shoppers on the amount that they spend on company goods in retail stores and online over the next year. The first study is run on a group of N = 1,000 men and yields an estimated ATE of catalogues on sales of $8.00 with a standard error of $3.00, which is statistically significant at p < 0.05. The second study is ran on a group of N = 250 women and yields an estimated ATE of catalogues on sales of $7.00 with a standard error of $6.00, which is not statistically significant. Every other aspect of the studies are the same (e.g., sampling, measurement, treatments, and implementation process).

Your data science team presents this data and claims that “sending these catalogues only works for men; for women, the effect is zero.” Critically evaluate this claim. (Note: you do not need to do any math to answer this question correctly. It is conceptual.)

3. Online Advertising [Total: 29 points] 社会科学作业代写

You are an employee of a newspaper and are planning a randomized experiment to demonstrate to Apple that online advertising on your newspaper’s website causes people to buy iPhones. Each site visitor shown the ad campaign is exposed to $0.10 worth of advertising for iPhones — that is, exposing a user to ads over the course of the week costs Apple $0.10 per person. You run a pretty popular newspaper, so there are 1,000,000 users available to be shown ads on your newspaper’s website during the one week advertising campaign. Apple truthfully indicates that they make a profit of $100 every time they sell an iPhone and that 0.5% of visitors to your newspaper’s website buy an iPhone in a given week in general, in the absence of any advertising.

Question a) First, a simple economics question that is not about statistics. By how much does the ad campaign need to increase the probability of purchase in order to be “just worth it” and a break-even ROI? Define ROI as [expected additional profit made as a result of advertising to each person – cost of advertising to each person]/cost of advertising to each person X 100 %. “Break-even” ROI would mean 0% ROI. [4 points]

Question b)

You expect the true effect of your ads is an increase in iPhone sales of 0.4percentage points. (For example, an increase from 0.5% conversion (the baseline) to0.8%conversion is 0.8 – 0.5 = 0.3 percentage points.) If your expectation is correct, what would be Apple’s ROI on the ads? [4 points]

Question c) Again, assume the true effect is an increase in sales of 0.4 percentage points. You want to figure out whether this experiment will yield an answer that is precise enough that you’ll be able to make Apple abandon their skepticism that the ads are not ROI- positive. To simplify things, suppose you expect your experiment will give you exactly theright answer, of 0.4 percentage points. 社会科学作业代写

If users are split 50:50 between the treatment group (exposed to iPhone ads) and control group (exposed to unrelated advertising or nothing; something you can assume has no effect on iPhone sales), what will be the confidenceinterval of your estimate on whether people purchase the phone? Express this confidence interval in percentage point terms — that is, what the confidence interval will be on the percentage point increase in the probability of purchasing an iPhone. (For example, an increase from 0.5% to 0.8% is 0.8 – 0.5 = 0.3 percentage points.) [8 points]

Note: The standard error for a two-sample proportion test is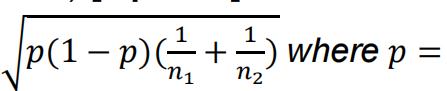

where x and n refer to the number of “successes” (here, the total number ofpurchases) over the number of “trials” (here, the total number of site visits). Here, 1 and 2 would refer to the treatment and the control groups (order is irrelevant). You can think of p as the average proportion of site visitors who make a purchase in the entire sample, averaging across treatment and control. The length of each side of a 95% confidence interval is calculated by multiplying the standard error by 1.96.

We would suggest using R as a calculator to make the math easier. Note: sqrt() is the function in R to compute a square root.

Question d)

Take the confidence interval you found in part (c) and express it in ROI terms.[4 points]

Question e) Is this confidence interval precise enough that you would recommend running this experiment? Why or why not? [3 points]

Question f) In experiments, we don’t need to randomly assign people to treatment and control groups 50/50. We can also randomly assign more people to one group than another, as long as to which group each person assigned remains random.

Exploiting this fact, the Chairperson of Board of Directors at the newspaper, worried about potential loss of revenue by not advertising to the control group, says she is not willing to hold back a control group any larger than 0.2% of users and says you should run the experiment with a 0.2% control group (that is, with only 1,000,000 * 0.002 = 2,000 people in the control group). In ROI terms, what would be the confidence interval for this same experiment if only 0.2% of users were placed in the control group and the remaining 99.8% in the treatment group? Given this, would you recommend running this experiment? Why or why not? [6 points]

4. Sportscard auctioning [Total: 33 points]

Conventional wisdom in Silicon Valley holds that some of the most profitable and successful startups run marketplaces, matching buyers and sellers and taking something off the top of their transactions — think Airbnb, Uber, eBay, etc. There are often multiple ways to set the prices and commissions buyers and sellers will pay. The impact of different pricing models can have huge implications for a business’ profitability. Randomized experiments can allow businesses to estimate the impact of their pricing models on profitability instead of just guessing at what pricing model is best.

Here we will consider how one industry tried to determine what pricing model was best. Suppose you are running a marketplace for sportscards — in particular, you run auctions for sportscards where you sell off multiple of the same card at once. There are many ways to run an auction like this, as multiple people can “win.” For example, perhaps for each of 2 cards there are 8 bidders, with the top 2 bidders winning. But how much do they pay if they win? 社会科学作业代写

One common approach to set the prices of the two cards is to have both winners pay an amount equal to the amount of the third-highest bid (that is, the highest losing bid). This is called a uniform-price auction. Another auction format is called a Vickrey auction, where people pay the next highest bid to their own. This means if you placed the highest bid you would win and you would pay the second highest bidder’s amount, instead of the third highestbidder’s amount. These auctions produce different incentives for bidders, who might bid below their true valuation strategically.

What is the impact of auction format on the auction’s clearing price?

In particular, which of these two auction formats will result in higher clearing prices? On canvas, you will find a set of data from an auction experiment that examined just this by John List and David Lucking- Reiley (2000). In this experiment, the researchers invited consumers at a sportscard trading show to bid against one another bidder for a pair of trading cards.

Sportscards vendors faced a choice identical to what is described above. For the purposes of this problem, suppose thevendors had previously used Vickrey auctions, but for the experiment they randomly assigned whether they used the Vickrey and uniform-price auction for each card. In the data linked above, the treatment auction format (denoted by uniform_price_auction = 1) is the multi-unit format. This was theoretically predicted to produce lower bids than the control auction format (denoted by the same = 0), the Vickrey format. We provide you a relevant subset of data from the experiment. 社会科学作业代写

Question a) Estimate the ATE of using a multi-unit auction (rather than a Vickrey format) on bids. [4 points]

Question b) you confront a skeptic who believes that auction format has no effect on anyone’s bids. Simulate the distribution of estimates one might reach by chance in the observed data under the assumption that this skeptic is correct. Plot them using hist() and then place an abline(v=estimated.ate) where the estimated ATE is, using your estimate from part a). [6 points]

Question c)

Compare the observed ATE estimate to the distribution from part b): compute the p-value. Note that if you have a negative ATE estimate, you’ll want to compute what share of the estimates under the null hypothesis are even smaller than the negative estimate. (For those of you who are aware of two-tailed p-values, you can ignore the idea of a two-tailed p- value for now.) [6 points]

Question d) In plain language, what does this p-value mean? What does it lead you to conclude? [6 points] 社会科学作业代写

Question e) Compute a 95% confidence interval for the average treatment effect estimate(the difference between the treatment mean and the control mean), using the R function t.test.It will yield the confidence interval. The t.test function spits out the confidence interval for you. (Because it relies on different assumptions, you might get slightly different confidence intervals using the t.test functions as the method we saw in class of computing the standard deviation of the sampling distribution.) [6 points]

Question f) In plain language, what does this confidence interval mean? [5points]

合作平台：essay代写论文代写写手招聘英国留学生代写