PROBLEM 1: MOLECULAR THERMODYNAMICS OF PURE FLUIDS
留学生math作业代做 Using the information you found in part d, create a cleaned-up version of the P-v diagram that you had plotted in part b.
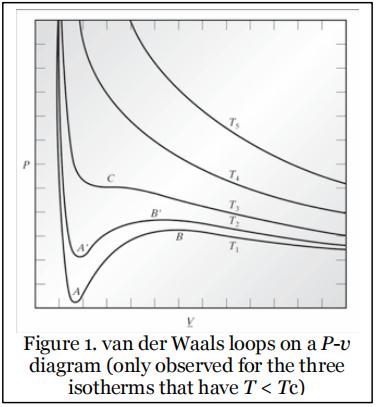
Recall from CBE40C: The behavior of most pure fluids can be described by cubic equations of state. When one such equation of state is used to plot isotherms on a P–v diagram (v is the molar volume in this problem, denoted as V in other literature), for T < Tc, a van der Waals loop is observed (see Figure 1, which is reproduced from Figure 7.3-1 in Chemical, Biochemical, and Engineering Thermodynamics by Stanley Sandler, 4th Edition).
These are regions of the phase diagram that a vapor phase and a liquid phase can coexist. However, as you also know from CBE40C, for each temperature T < Tc there is only one unique pressure, Psat, at which a gas liquid coexistence is possible. At this temperature and pressure, the fugacities of the vapor and liquid are going to be equal to one another, and this is the criterion that is used for finding Psat for a given T (or Tsat for a given P). The purpose of this problem is to use this criterion to find out what the Psat of NH3 is for a number of different temperatures, using two different equations of state.
Recall that cubic equations of state can be generalized in terms of the compressibility factor, Z, as: 留学生math作业代做
Z 3 + a Z 2 + b Z + g = 0
For the entire range of temperatures and pressures corresponding to the van der Waals loop, the cubic equation of state predicts three distinct, real roots. As you know, the middle root corresponds to the middle part of the loop,which is a physically unrealistic region (it predicts that pressurizing a fluid increases its molar volume), so that root is discarded.
Of the two roots remaining, the small one is the liquid compressibility, ZL, and the large one is the vapor compressibility, ZV. Those roots can then be used to calculate the fugacities corresponding to the predicted vapor and liquid phases, fV and fL, respectively. If those two fugacities are equal, the temperature and pressure that were used in the calculations correspond to the correct [T, Psat] pair (in other words, for any given T, the P that gives equal fugacities for the vapor and the liquid phases is the correct Psat).
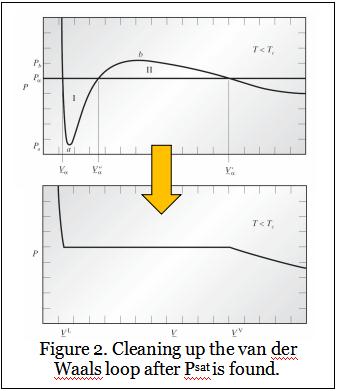
Once the correct Psat is found, the van der Waals loop can be cleaned up as shown in Figure 2 (previous page), which is reproduced from Figures 7.3-2 and 7.3-3 in Chemical, Biochemical, and Engineering Thermodynamics by Stanley Sandler, 4th Edition.
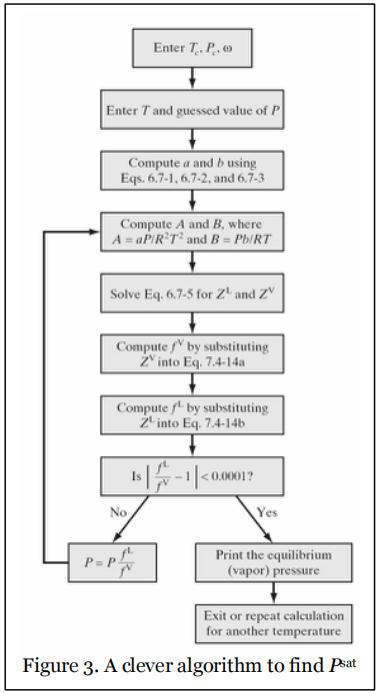
Now, how do we go about using this information to find Psat for a given T using a cubic equation of state? In principle, you can keep guessing different values of P, calculating fV and fL, and comparing them, until you find a P for which fV = fL. But this is not a very efficient method. Instead, Figure 7.5-1 in Chemical, Biochemical, and Engineering Thermodynamics by Stanley Sandler, 4th Edition, which is reproduced in Figure 3, gives a clever algorithm for finding Psat. It basically says that after the calculation of fV and fL, if they are not equal to each other to within a certain tolerance that you desire, then multiply your current guess of P by fL/fV and repeat the calculations iteratively.
In this problem, you want to create a function file that takes in a fugacity equation corresponding to an equation of state with its parameters for a given fluid, a value of T, and a value of P as an initial guess, and then goes through this clever algorithm to find the correct Psat for the given T. You then want to use this function file to find Psat for NH3 for a number of different temperatures, using two different cubic equations of state.
The temperatures that we want to find Psat for are T1 = 375 K, T2 = 382 K, T3 = 391 K,T4 = 400 K. We want to use the Peng-Robinson equation of state, and the van der Waals equation of state. Let us go through those two equations of state now:
1) van der Waals: 留学生math作业代做
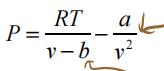
The parameters for ammonia are a = 0.4253 Pa.m6/mol2, b = 3.737 ´ 10–5 m3/mol If represented in terms of the compressibility factor:
Z3 +αZ2 + βZ +γ = 0
The parameters are given as:
α = −1− B β = A γ = − AB
where Z=Pv/RT is the compressibility factor, and the parameters A and B are given by:
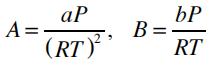
The fugacity of the vapor and the liquid phase can be calculated by:
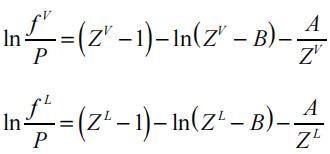
Here, ZL and ZV correspond to the liquid (low) and vapor (high) roots of the cubic equation of state, respectively.

2) Peng-Robinson
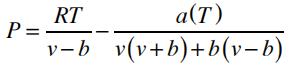
The relevant parameters are related to the fluid’s critical properties:
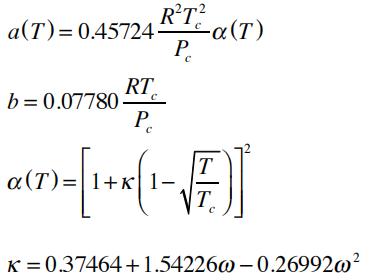
If represented in terms of the compressibility factor:
Z3 +αZ2 + βZ +γ = 0
The parameters are given as:
α = −1+ B,β = A− 3B2 − 2B ,γ = − AB + B2 + B3
where Z=Pv/RT is the compressibility factor, and the parameters A and B are given by:
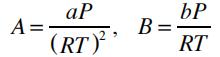
The fugacity of the vapor and the liquid phase can be calculated by:
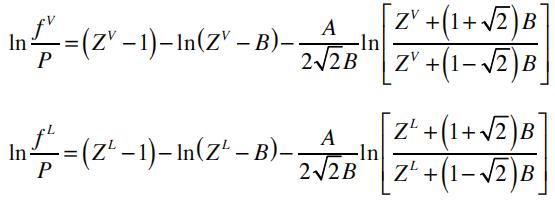
Here, ZL and ZV correspond to the liquid (low) and vapor (high) roots of the cubic equation of state, respectively.
The critical properties of ammonia can be found from thermodynamic tables:
Tc = 405.6 K, Pc = 11.28 MPa, w = 0.250
a) Develop a function file that takes in as input a function file for the fugacity calculation corresponding to any equation of state with any parameters needed in the fugacity equation, a value of T, and a P0 as an initial guess, and implements the clever algorithm shown in Figure 3 to find the correct Psat for the given T (with the tolerance as specified in Figure 3).
So the inputs to your function file should be a function handle referencing a function file for the fugacity equation with any parameters needed, and T and P0.
The output from the function should be Psat. Call this function file psatfinder. Note that psatfinder should be set up in a general way, so that it can work with both P-R and vdW equations of state (in fact, it will work with any cubic EoS as long as the fugacity equation is also known for that EoS).
b) Using the Peng-Robinson EoS, produce a log-log P–v diagram (v on the logarithmic x- and P on the logarithmic y-axis) for NH3 for temperatures T1 = 375 K, T2 = 382 K, T3 = 391 K, T4 = 400 K, T5 = 405.6 K, T6 = 408 K (all on one graph). Rescale your axes to 3 ´ 10–5 m3/mol £ v £ 1 ´ 10–3 m3/mol, and 1 ´ 106 Pa £ P £ 1 ´ 108 Pa. This plot should give you some guidance on how to guess your pressures in the next step.
c) Write a script file that sends the fugacity function file for the van der Waals EoS to psatfinder with the four different values of temperature T1, T2, T3, and T4 specified earlier, to find the corresponding Psat for each value (for NH3).
The entire script file should run with one command called PsatvdW, printing a column of the four T values and their corresponding Psat values at once. Note: you should find Psat for the temperatures given one by one, using a loop. 留学生math作业代做
d) Write a script file that sends the fugacity function file for the Peng-Robinson EoS to psatfinder with the four different values of temperature T1, T2, T3, and T4 specified earlier, to find the corresponding Psat for each value (for NH3). The entire script file should run with one command called PsatPR, printing a column of the four T values and their corresponding Psat values at once. Note: you should find Psat for the temperatures given one by one, using a loop.
e) BONUS QUESTION (10% extra on problem): Using the information you found in part d, create a cleaned-up version of the P–v diagram that you had plotted in part b.
NOTE: In Matlab, the command “isreal(a)” is a logical statement (True/False, or 1/0),regarding whether a number is real. You can use this command with an “if” statement to check if a number is real or imaginary. For example, check the commands “isreal(5)”,“isreal(2+0i)”, and “isreal(3+0.1i)”.

