COMS 4995: Intro Networks & Crowds
留学生CS代写价格 Each of them contains 80 percent of edges randomly selected from G. After selection, the node IDs in two smaller graphs are randomly shuffled.
Homework #2 – Reconciliation
Why there is three parts in this assignment: Each part fulfills one of the objectives of the class:
- Manipulateconcepts: Getting Familiar with the technical concepts used in class, by reproducing similar Being proficient by manipulating the object to answer some small-size problem.You are expected to answer this question rigorously, the answer can be quite short as long as it contains all the required argument to justify your answer.
- Experience the concepts in real case: Being able to reproduce these concepts on real or synthetic data. Study their properties in real
- Connectthe concepts to real-life: Interpret a problem you find in light of the notions you have Develop some critical eye to determine how the concepts introduced are useful in practice.
How to read this assignment : Exercise levels are indicated as follows
(↣) “elementary”: the answer is not strictly speaking obvious, but it fits in a single sentence, and it is an immediate application of results covered in the lectures.
Use them as a checkpoint: it is strongly advised to go back to your notes if the answer to one of these questions does not come to you in a few minutes. 留学生CS代写价格
(↷) “intermediary”: The answer to this question is not an immediate translation of results covered in class, it can be deduced from them with a reasonable effort.
Use them as a practice: how far are you from the answer? Do you still feel uncomfortable with some of the notions? which part could you complete quickly?
(↬) “tortuous”: this question either requires an advanced notion, a proof that is long or inventive, or it is still open.
Use them as an inspiration: can you answer any of them? does it bring you to another problem that you can answer or study further? It is recommended to work on this question only AFTER you are done with the rest!
Part A — Manipulating the Concepts 留学生CS代写价格
Exercise 1: Assembling a Network from Egonets (13 pt)
Motivation: Imagine you are a student in the advanced Social Networks course offered only to graduate students. George, one of your classmates, is doing a research project on alcohol consumption, and he asks everyone in the class to participate in it. In order to perform his research, George asks everyone to provide information on the number of drinks they have had with their classmates (including specific names) within the last month and assures that this information would be strictly confidential.
For example, if Alex and Sam met once and they had three rounds of drinks, and a week later they met for another round, then Alex would indicate that he had 4 drinks within the last month with Sam and Sam would do the same. After all answers are collected, George creates a network reflecting drinking relationships among his classmates. Since he is examining individual patterns of drinking, egonets are of special interest for testing his hypotheses. 留学生CS代写价格
George believes that he has interesting findings and looks forward to presenting them to his classmatesat the end of the semester. During the presentation, George shows the egonets obtained from the originalnetwork in an anonymous manner (see Figure 1), and claims that it is impossible to identify the structure of the whole network and specific individuals. Nonetheless, one student argues that it is actually very easy to assemble the initial network using this information, which provokes a heated discussion in the class since students were promised confidentiality. This exercise leads you through a series of questions to resolve this discussion.
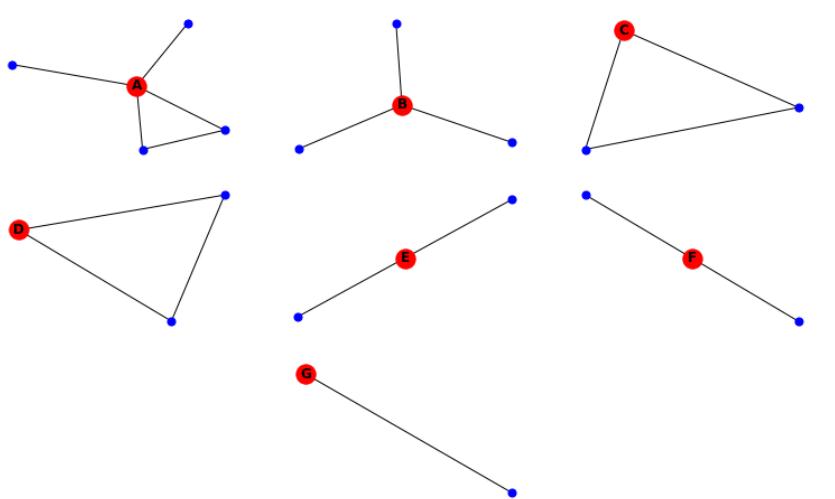
Figure 1: Egonets extracted from the network of drinking relationships.
1.(↣)Can you identify the number of edges in the original network just from the information provided in the Figure 1?
2.(↷) Is it possible to reconstruct the original network just from the egonets? Is it uniquely identi- fiable? If yes, explain If no, provide at least two networks that have this underlying structure ofegonets. 留学生CS代写价格
3.(↷) Suppose you have additional information that A is connected to B. Would your answer to the previous question change? Explain your reasoning.
4.(↷)Suppose students in the class drink just in pairs (maximum two people per round), and the information on total number of drinks each student had with his/her classmates within the last month is known (see Table 1):
| Student | A | B | C | D | E | F | G |
| # rounds | 31 | 19 | 26 | 21 | 6 | 7 | 10 |
Table 1: Total joint alcohol consumption between the classmates.
Moreover, assume that it is known that student E had the same number of drinks with both connections. Using the network from question 1.3 (pick any, if there are several of them), provide the number of drinks that each connected pair of students had together.
5.(↷) Now you still have data on total alcohol consumption of each individual (Table 1) and addi- tional info about student E, but the assumption of drinking in pairs is removed. That is, people candrink in groups that consist of more than two Identify the number of drinks each group (of two or more people) had together or explain why it is not possible to do so.

Exercise 2: Joining an unbalanced world (8 pt) 留学生CS代写价格
In this exercise, we will learn whether a node can easily join an unbalanced world. We consider a graph tt = (V, E+, E−) that contains positive and negative edge and is complete (i.e., all pairs of nodes have one edge between them). It is said balanced if all triangle contains either 1 or 3 friendship edges.
Imagine a new person X joins the graph tt and has a complete freedom in deciding whether she maintains a positive or negative relationship with anybody else in the graph. The question is whether shecan do so while not being involved in any unbalanced triangle herself. That means the following, if tt isbalanced, then X wants to join the graph while making sure she does not break this property. Otherwise, if tt is already not balanced, some “forbidden triangles” exist, but at least X would like to make sure that after joining she is not part of any “forbidden triangles” herself.
1.(↣) Show by hand that if the graph tt contains up to three nodes and is balanced, X can join the graph and not create any unbalanced triangle.
2.(↷) Using a result from the class, prove that for a balanced graph of any size, then it is possible for X to always do so.
3.(↷)Assuming now that tt contains 3 nodes and is not balanced, what is the best thing that X can do to join the graph and not be part of any unbalanced triangle?
For all cases of tt, you should either prove that it is possible by providing a solution, or give a proof that it is impossible. We encourage that you provide a concise explanation instead of the result of an exhaustive search. 留学生CS代写价格
- (↣)Provide a general conclusion describing in which cases X can successfully join any graph tt and not be part of unbalanced triangle?
Briefly discuss how this result generalizes when you use another definition of “balanced”, generally called weakly balanced, in which triangles with three enemies are allowed, and the only triangles to avoid are the one with exactly two edges with positive signs.
Part B — Experiencing the Concepts 留学生CS代写价格
Exercise 3: Identifying Users with Degree and Edge Information (15 pt)
Motivation: In this problem we explore how to use degree and connection information to identify individuals.
Description We use the data set: http://snap.stanford.edu/data/ca- GrQc.html , the dataset we used for Exercise 1. Please make sure to pre-process the graph using the given code so that the degree information is correct. The general setting is as follows: let the graph be tt = (V, E), where V is the set of nodes (vertexes) and E the set of edges (without self-loops); d : V → Z+ maps from a vertex to the vertex degree, i.e. d(x) is the degree of x.
Alice is an agent who will host a one-time meeting for a set of users X = {x1, x2…xk} ∈ X (X will be different for each problem),
and will carelessly leak the information of D = [d(x1), d(x2)…d(xk)]. Eve wants to figure out the participants of the meeting based on the information D, tt and X ; if Eve can uniquely recover the entire X based on D, tt and X , we say that the meeting for the set of participants X is unsafe; if a user x belongs to any such unsafe meeting X ∈ X , we say that the privacy of x might be compromised. Please print the list of users whose privacy is compromised into 2-1.txt, 2-2.txt, 2-3.txt, 2-4.txt respectively, one on each line.
- (↣) Assume that Alice will only host a meeting of one user, i.e. X = {X|X ⊂ V, |X| = 1}. How many users’ privacy might becompromised?
- (↣) Assume that Alice will only host a meeting of two users, i.e. X = {X|X ⊂ V, |X| = 2}. How many users’ privacy might becompromised? 留学生CS代写价格https://uhomework.com/%e7%95%99%e5%ad%a6%e7%94%9fcs%e4%bb%a3%e5%86%99%e4%bb%b7%e6%a0%bc/
- (↷) Assume that Alice will only host a meeting of two connected users, i.e. X = {{x1, x2}|(x1, x2) ∈ E}, and Eve knows that Alice will host a meeting only for connected users. How many users’ privacy might becompromised?
- (↬)Assume that Alice will only host a meeting of three mutually connected users and Eve knows thatAlice will host only such How many users’ privacy might be compromised?
- (↷) What do you observe? (pretty open questions; write whatever seems significant toyou)
Exercise 4: Identifying users from different social networks (15 pt) 留学生CS代写价格
Motivation: Many people have multiple social network accounts, but these accounts almost always connect to the same group of people that they know from real life. Given a small amount of identification links between two networks as ground truth, we wonder whether it is possible to figure out who is who in the underlying graph of social relationships.
Description: This problem asks you to implement a simplified version of the reconciliation algorithm with given data sets and instructions. G1 and G2 are two graphs derived from a master graph G. Each of them contains 80 percent of edges randomly selected from G. After selection, the node IDs in two smaller graphs are randomly shuffled. If node i in G1 and node j in G2 correspond to the same node in the master graph, (i,j) is called an identification link. (G1 and G2 are undirected graphs and the order of nodes in an identification link matters). You are provided with 400 identification links to start with. Thegoal of this exercise is to find as many identification links as possible using score based on the number ofsimilarity witnesses. Please, find the data sets in ‘hw2Ex3.zip’ file in the Resources section on Piazza.
Deftnition of similarity witnesses:
A pair of nodes (u1, u2) with u1 ∈ tt1, u2 ∈ tt2 is said to be a similarity witness for a pair (v1, v2) with v1 ∈ tt1, v2 ∈ tt2 if u1 ∈ N1 (v1), u2 ∈ N2 (v2) and u1 has been linked to/identified with u2, where N (i) is a set of neighbors (direct connections) of node i.
- (↣)Use the number of similarity witnesses as similarity How many pairs of nodes (i, j), i ∈ tt1, j ∈ tt2 have similarity score that is not less than 25? Please, print out these links and save them in the file ‘Ex3-1’ in the same format as the initial data set.
- (↷) Set threshold T = 13, find new identification links (in addition to initial 400 links) that have similarity score not less than T. Sort the additional identification links first by similarity score, then by id in G1, and lastly, by id in G2 in descending order. Add the links one by Run the process for T = 13 iteratively until you couldn’t find any additional identification links. Record and save them as ‘Ex3-2-13’. Reset everything. Run the same analysis with T = 16 and T = 11. Record and save all added links separately as ‘Ex3-2-16’ and ‘Ex-3-2-11’ respectively. (Hint: each node can be identified onlyonce.)
3.(↷) Find as many identification links as possible and save your results as ‘Ex3-3’.Hints:
- Setup an adaptive threshold.
- Construct your own testing graph from one of the graphs using known information.
- We would remove duplicated nodes before testing your results, so please don’t give us all the possible results.
- The most important evaluation metric is the number of correct identification links, but error rate is considered for grading as well.
- Havefun!
Part C — Concepts at large 留学生CS代写价格
Exercise 5: Paizzi and Classera walk into a bar … (12 pt)
Motivation: Data is often more valuable in combination. And there are plenty of cases of synergies between companies. Who knows? perhaps even a social networking service might have reasons to share data with a company specializing in assisting political campaigns to efficiently serve ads. In this exercise, we will suggest you reflect on the promises and perils of data-sharing.
Imagine you are in charge of growth at the academic forum start-up paizzi. As often, competition is fierce in any digital service, and other products (campuswire, slack) are gradually being adopted, especially by massive online classes such as classera. Paizzi has a strong market share in the formal academic market, including community colleges. You would like to use that strong position to tackle the growing market of online education, and a recent study found that many of ex-students of the academic colleges you serve are also taking such online classes after they use your service extensively. 留学生CS代写价格
- (↷) Write the email you would send to the head of the growth team at classera? You knowthatshe has a D in Computer Science and is a social network nerd. She will not decidto collaboratewith you on the basis of nice language, she will be looking for a project with scientific foundations.
- (↷)Based on your great answer above, the head of the growth team responds She even mentions that the company is interested in producing externally available research study with a publicly available resource of students’ ”trajectory through classes” to prove the concept of the synergy. She sets up a meeting with various divisions to discuss what are the requirements to get things done. Please describe the issues you will discuss with them?

