留学生统计代考 STAT 252代写

Department of Mathematical and Statistical Sciences STAT 252 – PRACTICE MIDTERM

Student Name:                             Signature:                                     

留学生统计代考 The density of the gastropod Terebralia palutris was investigated in four mangrove forests by throwing a quadrat at random points on the sediment.

Instructions: (READ ALL INSTRUCTIONS CAREFULLY.)  留学生统计代考

1. This is a closed bookexam.
2. You are permitted to use a NON-PROGRAMMABLE calculator, and the formula sheets and tables provided.
3. Please turn off your cellular phones or pagers.
4. You have 50 minutes to complete the exam.
5. The exam is out of a total of 33marks.
6. This exam has 9 pages (including this cover page and all computer output tables). Please ensure that you have all pages.
7. Make sure your name and signature are on this cover page and your student ID number is at the top of page two.
8. For questions that state you should show all steps, be sure that you do this in order to obtain full credit. Conclusions must also be clearly stated. Your answers must have adequate justification.
9. For other questions that say you do notneed to show all steps, read the question carefully and follow the exact instructions regarding what is  required.
10. If you run out of space in the blank area provided for each question, use the back of the page to complete your answers as needed and label such answers so that is clear which question they belong to.
11. You may also use the reverse sides of the pages for allrough work.
12. When referring to “log”, I am always referring to the natural log.

BEST WISHES!!

Student ID Number:                         

Question 1 (5 marks)  留学生统计代考

The owner of a fishing camp wanted to test the effectiveness of two brands of mosquito repellents (A and B). From the population of visitors he randomly allocated 12 visitors to use Repellent A and another 12 visitors to use Repellent B. All wore short-sleeved shirts and shorts. The table below shows the summary statistics for the number of bites each visitor had after fishing for 4 hours on the lake. Assume that the data are normally distributed. Note: You might not need all of the statistics shown. At the 5% significance level, carry out the most appropriate test to determine whether there is a difference in the mean number of bites between people who used the two brands. Show all steps of the hypothesis test.

Summary statistics	Brand A	Brand B 留学生统计代考	Difference
Average	25.08	21.42	3.67
Standard Deviation	8.51	6.68	14.37

There is no indication that the two samples are paired or related, therefore the two-mean test for independent samples should be used

H0: mBrand _ A – mBrand _ B = 0           Parameter: mBrand _ A – mBrand _ B

(There is no difference in the mean number of bites between people who used the two brands)

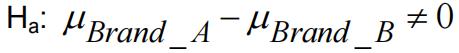
(There is a difference in the mean number of bites between people who used the two brands)

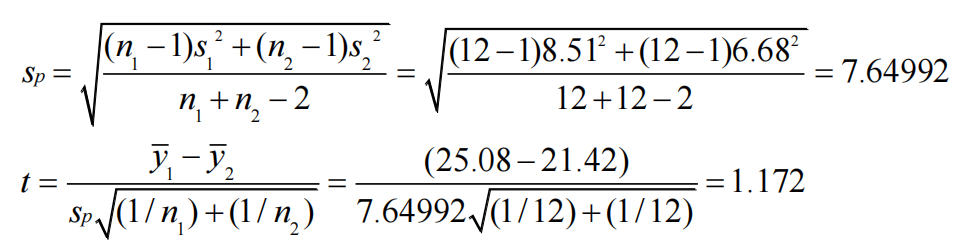
df = n1 + n2 – 2 = 12 +12 – 2 = 22      Thus, (0.15 > P > 0.10) x 2 ==> 0.30 > P-value > 0.20

There is weak evidence against H₀. Since P-value > α (0.05), do not reject H₀.

At the 5% significance level, the data do not provide sufficient evidence to conclude that there is a difference in the mean number of bites between people who used the two brands.

Question 2 (3 marks in total) 留学生统计代考

Suppose that analysis of log transformed data results in the estimate of the difference between the logged means of Treatment A and Treatment B to be 0.746 and a 95% confidence interval for the additive effect of treatment is between 0.218 and 1.278.

Define the parameter as: mLnB – mLnA .

(a)(2 marks) Back transform the estimate and the confidence interval to the original scale. Interpretthe meaning of this confidence interval on the original scale.

Back Transformation of the estimate and confidence interval to the original data gives the following: Estimate of the difference = e0.746 = 2.109

Lower endpoint of the confidence interval =  e0.218  = 1.244  留学生统计代考

Upper endpoint of the confidence interval =  e1.278   = 3.589

Therefore, a 95% confidence interval for the ratio of the medians on the original scale 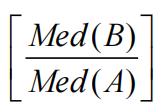is: (e^0.218, e^1.278 ) = (1.244,3.589)

OR

It is estimated with 95% confidence that the median effectiveness of Treatment B is between 1.244 and 3.589 times the median effectiveness of Treatment A.

(b)(1 mark) Based on the confidence interval you found in part (a), after back transformation, would you conclude that there is a difference between the medians for Treatment A and Treatment B (with 95% confidence)? Explain the logic of your answer.  留学生统计代考

Since the confidence interval after back transformation, which is (1.244, 3.589), does not contain 1, that means we can be 95% confident that there is a difference between the medians for Treatment A and Treatment B.

Question 3 (7 marks in total)  留学生统计代考

Based on a random sample of graduates who had just completed 4 different degree programmes (Bachelor’s degree in Civil Engineering, Bachelor’s degree in Mechanical Engineering, Master’s degree in Civil Engineering, and Master’s degree in Mechanical Engineering), information was gathered concerning their starting salaries. Assume that all required assumptions are satisfied for applying the analyses needed to answer parts (a) and (b) below. Use the parameters defined below and the computer output in Tables 1 – 4.

The parameters are already defined for you as follows:

mB–Civil = Bachelor’s degree in Civil Engineering

mB–Mech = Bachelor’s degree in Mechanical Engineering  留学生统计代考

mM –Civil = Master’s degree in Civil Engineering

mM –Mech = Master’s degree in Mechanical Engineering

Table 1: Summary statistics of the salaries of the 4 groups.

Descriptives

Salary

留学生统计代考	N	Mean	Std. Deviation	Std. Error	95% Confidence Interval
					Lower Bound	Upper Bound
Bachelor’s Civil	5	30.400	2.6334	1.1777	27.130	33.670
Bachelor’s Mechanical	5	35.800	3.3705	1.5073	31.615	39.985
Master’s Civil	5	35.620	3.5181	1.5733	31.252	39.988
Master’s Mechanical	5	42.280	3.8745	1.7327	37.469	47.091
Total	20	36.025	5.3195	1.1895	33.535	38.515

Table 2: The overall ANOVA table for comparison of the salaries of the 4 groups.

ANOVA

Salary

	Sum of Squares	df	Mean Square	F	Sig.
Between Groups	354.902	3	118.301	10.358	.000
Within Groups	182.736	16	11.421
Total	537.638	19

Table 3: ANOVA table for comparison of the salaries of Bachelor’s versus Master’s Degree holders (ignoring Civil versus Mechanical Engineering Majors). 留学生统计代考

ANOVA

Salary

	Sum of Squares	df	Mean Square	F	Sig.
Between Groups	171.113	1	171.113	8.403	.010
Within Groups	366.525	18	20.362
Total	537.638	19

Table 4: ANOVA table for comparison of the salaries of Civil Engineering versus Mechanical Engineering Majors (ignoring the type of degree, Bachelor’s versus Master’s).

ANOVA  留学生统计代考

Salary

	Sum of Squares	df	Mean Square	F	Sig.
Between Groups	181.805	1	181.805	9.197	.010
Within Groups	355.833	18	19.769
Total	537.638	19

(a)(1 mark) A university student planning his career heard that people with Master’s degrees in mechanical engineering are in great demand.

Develop a linear combination (contrast) to test if there isa difference between the starting salary of those with a Master’s degree in Mechanical Engineering compared to the other three degrees (i.e., Bachelor’s degree in Civil Engineering, Master’s degree in Civil Engineering and Bachelor’s degree in Mechanical Engineering, combined). You do not need to do anything further; just define the contrast.

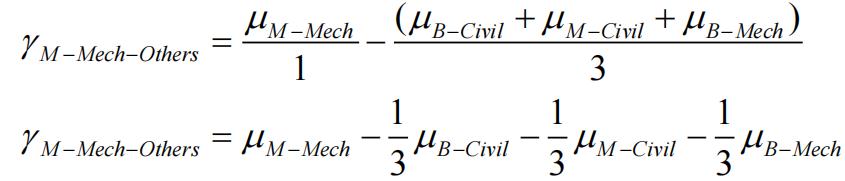
(b)(6 marks) Another university student planning his career suspected that any difference in salary would be mainly due to the major he decided to study, regardless of whether he finished with a Bachelor’s or Master’s degree. At the 5% significance level, perform the most appropriate test(a single overall test), showing all steps, to determine whether there is a difference between the salaries of civil and mechanical engineers, after accounting for the effect degree (Bachelor’s versus Master’s).

If there is no effect of major (Civil versus Mechanical) for Bachelor’s degrees, then: mB–Civil = mB–Mech

If there is no effect of major (Civil versus Mechanical) for Master’s degrees, then: mM –Civil = mM –Mech  留学生统计代考

H0 : mB–Civil = mB–Mech

and

mM –Civil = mM –Mech

[Reduced model: Two means model only for Bachelor’s and/or Master’s]

Ha : mB–Civil , mB–Mech , mM –Civil , mM –Mech

[Salaries are not all the same for the different Majors/Degrees] [Full model: Four means model]

Using the ANOVA table for the comparison of all four means (Table 2: Full model = Four means model) And the ANOVA table for Bachelor’s versus Master’s (Table 3: Reduced model = Two means model)

F = [SSE (reduced ) – SSE ( full)] [dfE (reduced ) – dfE ( full)]

SSE ( full) / dfE ( full)

= [366.525 -182.736] [18 – 16] = 183.789 / 2 91.8945 = 8.046

182.736 / 16 182.736 / 16 11.421

For the Extra-Sum-of-Squares F-test, df   留学生统计代考

= (Extra df , n – k ) = (2,16)

Thus, 0.005 > P > 0.001, which provides very strong evidence against the null hypothesis. Since P < α (0.05), reject H₀.

Conclusion: At the 5% significance level, there is sufficient evidence to conclude that there is a difference between the salaries of civil and mechanical engineers, after accounting for or eliminating the effect degree (Bachelor’s versus Master’s).

Question 4 (6 marks in total)

An experiment was conducted in which a random sample of 44 students were allocated at random to four groups. Each group was subjected to four learning methods as follows: L = lecture only, L+C = lecture and computer labs, L+C+A = lecture, computer labs and assignments, L+A 留学生统计代考

= lecture and assignments. All four groups had the same instructor for all components of the course and all other conditions were kept constant for all groups. The output below is from an ANOVA F-test which resulted in rejecting the null hypothesis and concluding that not all mean scores for the four learning methods were equal.

Descriptives

Scores

	N	Mean	Std. Deviation	Std. Error	95% Confidence Interval for Mean
					Lower Bound	Upper Bound
L	11	4.82	1.601	.483	3.74	5.89
L+C	11	6.18	1.168	.352	5.40	6.97
L+C +A	11	7.09	1.136	.343	6.33	7.85
L+A	11	5.36	.924	.279	4.74	5.98
Total	44	5.86	1.472	.222	5.42	6.31

ANOVA

Scores

	Sum of Squares	df		Mean Square	F	Sig.
Between Groups Within Groups Total	32.455 60.727 93.182		3	10.818 1.518留学生统计代考	7.126	.001
		40 43

Contrast Coefficients

Contrast	Method
	1	2	3	4
1	.5	-.5	-.5	.5
2	.5	.5	-.5	-.5
3	1	-.33	-.33	-.33
4	-.33	-.33	1	-.33
5	-.33	-.33	-.33	1

 Contrast Tests

		Contrast	Value of Contrast	Std. Error	t		df		Sig. (2-tailed)
1 2 Assume equal Scores 3 variances 4 5			-1.55 -.73 -1.33a 1.69a -.61a 留学生统计代考	.372 .372 .428 .428 .428	– –	4.160		40		.000
						1.958		40	.057 .003
					-3.112		40
					–	3.952		40		.000
						1.417		40		.164

(a)(3 marks) Using the Bonferroni Method, at the 94% confidence level, calculate the individual comparison-wise error rate ( aI ), find the critical value (two-sided) from the appropriate statistical table and calculate the margin of error. You do not need to perform the other steps. [Note: You only have to calculate the margin of error once since the sample sizes are equal for all treatment ]

The number of multiple comparisons (m) that are possible is:

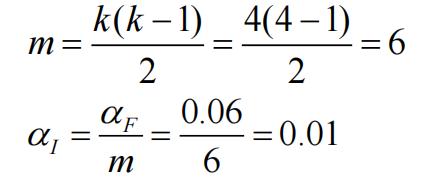
The Critical value of t at df = n – k = 44 – 4 = 40 for a  /2 = 0.005 is: t = 2.704

The margin of error (ME) for each comparison (group i vs. Group j):

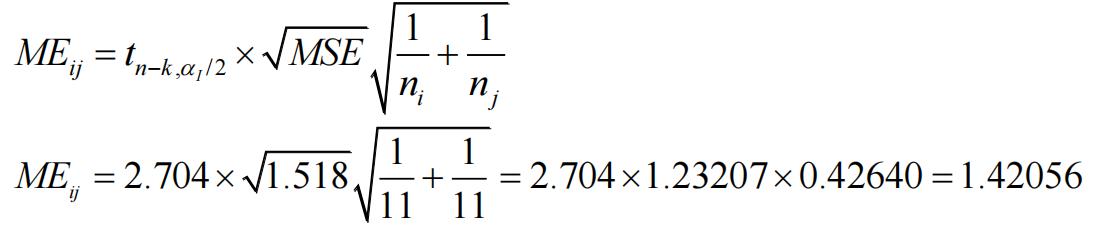
(b)(4 marks) The researcher suspected that the effectiveness of Method 3 (combining lecture,computer labs and assignments) is different from the effectiveness of all the other learning methods. Develop this linear combination (contrast) to test the researcher’s prediction. Perform the test at the 5% significance level, showing all steps. However, for the calculations step make use of the contrast tables in the SPSS output above. Be sure to state the number of the contrast you have selected.

[Sum of the coefficients = 0]

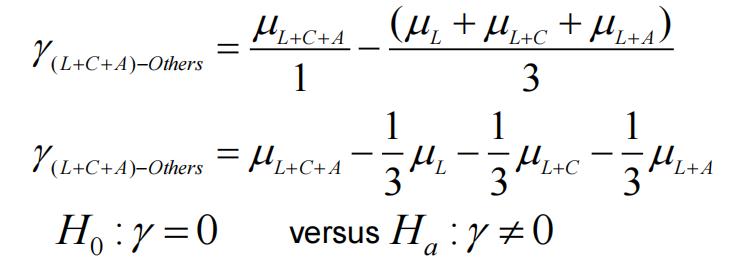
In the table of contrast coefficients, this is Contrast 4. 留学生统计代考

Estimate of contrast 4 is: γ = 1.69

Standard error of the estimate is: SE(γ) = 0.428

The t-statistic is:

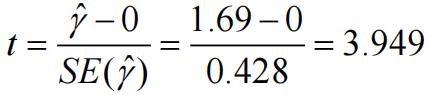
df = n – k = 44 – 4 = 40

P < (0.0005 x 2), so P < 0.001

There is extremely strong evidence against H₀. P < α (0.05), therefore reject H₀.

Conclusion: At the 5% significance level, there is sufficient evidence to conclude that there is a difference in effectiveness between Method 3 and all the other learning methods.

Question 5 (4 marks) 留学生统计代考

Three strains of cultured Staphylococcus aureus (bacteria that cause staph infections) were observed and bacterial counts (in millions) were recorded, obtaining summarized data and One-Way ANOVA output as shown below. At the 1% significance level, perform the most appropriate test (showing all steps) to determine whether there is a difference in mean bacterial counts between the three strains (that is, determine whether at least two means are different).

SUMMARY STATISTICS
Groups	Count	Sum	Average	Variance
Strain A	5	100	20	52
Strain B	5	117	23.4	34.3
Strain C	5	182	36.4	21.3

One-way ANOVA table		留学生统计代考
Source of Variation	SS	df	MS		F		P-value
Between Groups	749.2	2	374.6		10.44424		0.00236
Within Groups	430.4	12	35.8667
Total	1179.6	14

H₀: µ₁ = µ₂ = µ₃ (One-mean model)

There is no difference in mean bacterial counts between the three strains.

H_a: µ₁ , µ₂ , µ₃ (Three-mean model)

Not all the mean bacterial counts for the three strains are equal. (Or, there is a difference in the mean bacterial counts between at least strains.

k = number of populations being compare = 3 n = total sample size = 15

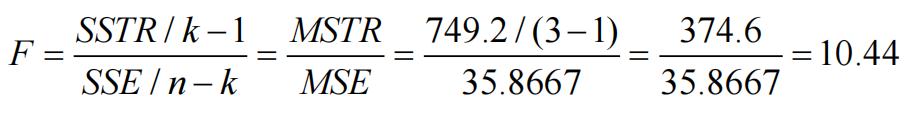
For df = (k – 1, n – k) = (2, 12) 0.005 > P > 0.001

There is very strong evidence against H₀. Since P-value < α (0.01), reject H₀.

At the 1% significance level, the data provide very sufficient evidence to conclude that there is a difference in the mean bacterial counts for the three strains (that is, at least two means are different).

Question 6 (5 marks)

The density of the gastropod Terebralia palutris was investigated in four mangrove forests by throwing a quadrat at random points on the sediment. At the 5% significance level, carry out the most appropriate test to determine whether there is a difference in density of these gastropods among the forests. The data shown below (in no./m²) are not normally distributed, nor are they lognormal. The observations have been ranked in order from lowest to highest. Explain the reasons why you have selected the test that you have decided to apply. Show all steps of the hypothesis test. 留学生统计代考

Mbweni		Ruvuma		Ruvu		Rufiji
(no./m2)	Rank	(no./m2)	Rank	(no./m2)	Rank	(no./m2)	Rank
10	11.5	105	20	0	2.5	7	9
0	2.5	0	2.5	122	21.5	10	11.5
28	16	35	17	5	8	43	18
122	21.5	0	2.5	27	15	281	24
2	6	8	10	2	6	150	23
		14	13	2	6	58	19
		20	14

The Kruskal-Wallis test is selected because the purpose of the research question is to test for the difference between more than two populations. Since the data are neither normal nor lognormal and sample sizes are less than 30 so, we cannot apply the Central Limit Theorem so the Kruskal-Wallis test is the only test that can be applied

H₀: There is no difference in abundance between any of the mangrove forests H_a: The abundance of gastropods is different between at least two of the forests.

R₁ = 57.5, R₂ = 79, R₃ = 59, R₄ = 104.5

n₁ = 5, n₂ = 7, n₃ = 6, n₄ = 6

n = 24

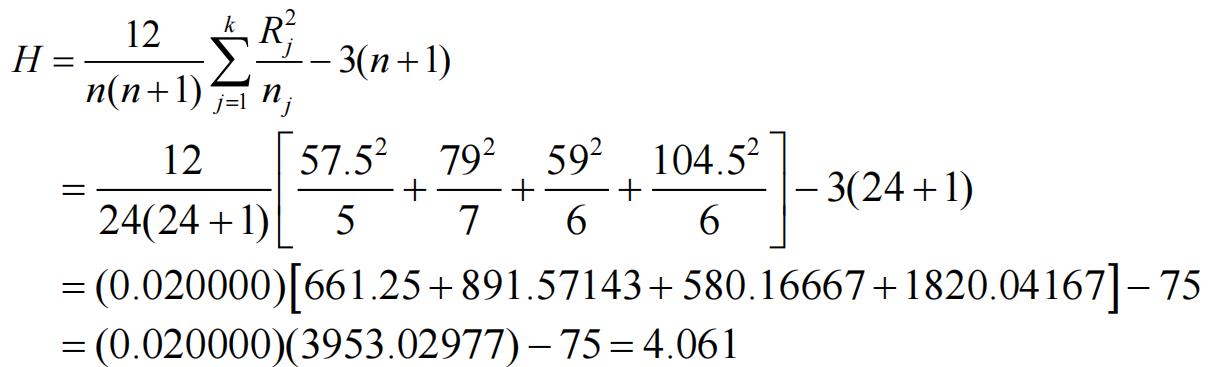
df = k – 1 = 4 – 1 = 3 Examining the Chi-square table, P > 0.20, so there is weak evidence against H₀. P > α (0.05), therefore, do not reject H₀.

At the 5% significance level, the data do not provide sufficient evidence to conclude that there is a difference in the abundance of gastropods among the mangrove forests.

Question 7 (2 marks) 留学生统计代考

In inferential statistics, what does it mean to be 95% confident?

It means that, if we took many random samples from the same population and calculated a confidence interval for each of those samples, chances are that 95% of those confidence intervals would contain the population parameter of interest (e.g., the population mean or the difference between two population means) that we are attempting to estimate.

更多代写：留学生计算机作业代写 留学生网课代考代做 留学生英国代写 留学生英文Essay代写 留学生英文Paper代写 商业essay论文代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写