Final Assessment for EEET 2206
留学生工程系代写 Question 2 and Question 3 require that you copy and paste your MAT-LAB and Simulink programs into the same document.
Instructions
- Your submission of the assessment paper consists of only one word document with your name and student number.
- Question 2 and Question 3 require that you copy and paste your MAT-LAB and Simulink programs into the same document. However, you do not need to include the MATLAB functions.QUESTION 1 Multiple Choices (30 marks)
QUESTION 1 Multiple Choices (30 marks)
- The Laplace transfer function of a continuous-time system is given by
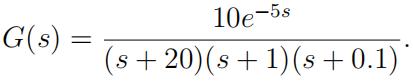
(a) The dominant time constant is 10, the steady-state gain is 5 and the time delay is 5.
(b) The dominant time constant is 20, the steady-state gain is 10 and the time delay is 5.
(c) The dominant time constant is 10, the steady-state gain is 1 and the time delay is 5.
(d) None of the above.
- The Ziegler-Nichols tuning rules with reaction curve can be applied to the following model:
(a) G(s) = 
, where Kss,τM and d are positive;
(b) G(s) = 
, where Kss,τM and d are positive;
(c) G(s) = 
, where Kss,τM and d are positive; 留学生工程系代写
(d) none of the above.
3.A proportional plus derivative controller has the Laplace transfer func-tion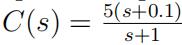 
. In order to implement this controller, the propor-tional control gain Kc, derivative gain τD and derivative fifilter τf are calculated as:
(a) Kc = 5, τD = 10 and τf = 1;
(b) Kc = 0.5, τD = 9 and τf = 1;
(c) Kc = 5, τD = 9 and τf = 1;
(d) none of the above.
- A nonlinear system is described by the following difffferential equation:
y¨(t) = 10y(t) 4 + 0.4u(t) 4
The operating condition for this system is chosen to be y 0 = 0 and u 0 = 1. The linearized model is(a) a second order system with both poles at 0;
(b) a third order system with poles at 0.2;
(c) a fourth order system with poles at 0.4;
(d) none of the above.
- The transfer function of a system is given by
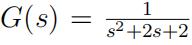and thecomplementary sensitivity function is
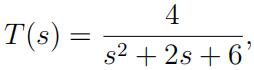
(a) the controller is C(s) = 
;
(b) the controller is C(s) = 4;
(c) the controller is C(s) = 2;
(d) none of the above.
QUESTION 2 (25 marks)
A continuous time system is described by the fifirst order plus delay transfer function
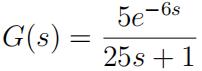
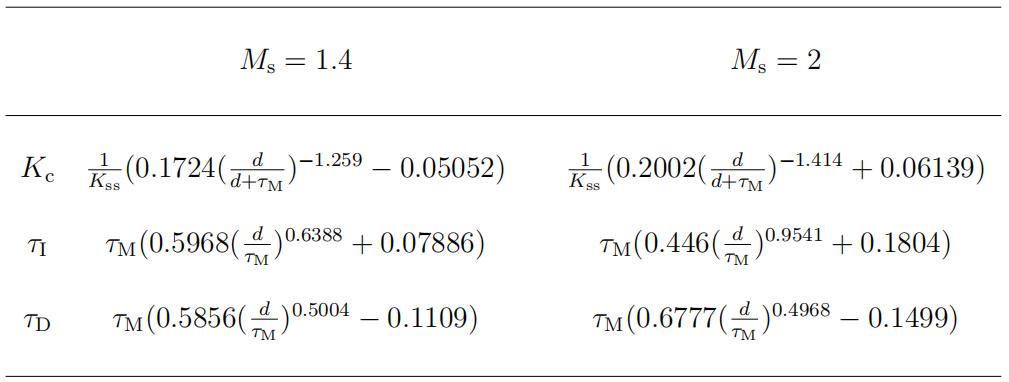
- (15 marks) Find the controller parameters Kc, τI and τD using the tuning rules given in Table 1, where Kss is the steady-state gain, τM is the time constant, d is the time delay and Ms = 1.4.
- (5 marks) Simulate closed-loop response with sampling interval ∆t =0.1 and simulation time Tsim = 600 (sec). A unit step reference signal enters the system at time t = 0 and an input disturbance with ampli-tude of one entering the system at t = 300 (sec). In the simulation,both proportional control and the derivative control are implemented on the output only. The derivative fifilter time constant is chosen to be 0.1τD. Plot the control signal and output signal.
- (5 marks) Let umax and umin denote the maximum and the minimum values of the control signal. What is umax? What is umin?
QUESTION 3 (25 marks) 留学生工程系代写
Design a PID controller with fifilter for the following system:
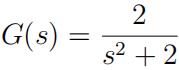
1. (10 marks) Choose the desired closed-loop characteristic polynomial
as (s 2 + 2ξwns + w 2n) 2 where ξ = 0.707 and wn = 3. What are the values of Kc, τI , τD and τf ?
- (5 marks) Simulate the closed-loop step response and input distur-bance rejection. In the simulation, the derivative control is imple-mented at the output, the reference signal r = 1 and the input dis-turbance has an amplitude of −3.5 entering the simulation at half of the simulation time. The sampling interval ∆t = 0.01 and the simula-tion time Tsim = 16. Present the output signal and control signal.
- (10 marks) Can you use pole-zero cancellation technique for the controller design? Explain your answer.
QUESTION 4 (20 marks) 留学生工程系代写
The desired reference signal for a system is given as
r(t) = 3sin(0.5t).
Design a resonant controller so that the output will track this reference signal without steady-state error. Here, the system is described by the following transfer function:
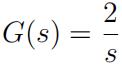
- (10 marks) Choose all the desired closed-loop poles to be −3.
- (10 marks) Use fifinal value theorem to show that the closed-loop control system will track a reference signal r(t) = sin(0.5t)+10 without steady-state error.Ms = 1.4
更多代写：法律专业课业代写 代考一般多少钱 代修网课加拿大 环境艺术类report代写 英国essay代写 加拿大经济学assignment代写
