Interconnection Networks
留学生代写assignment Consider the different orders in which these operations could be executed. Draw all possible trees that could result.
Problem 1. (9 points): 留学生代写assignment
You are building a packet switched logarithmic network for an eight-core processor. The logarithmic network is pictured below with the processors numbered 1 to 8 and the switches labeled A to L. Assume that a packet is 64 bytes.
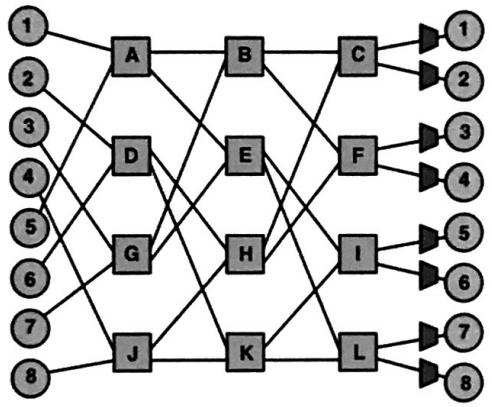
A. (3 pt)Is this network blocking? Ifit is, list two source-destination pairs that would block each other.
B. (3 pts) With store and forward routing, what is the minimum latency for sending a single packet from one processor to another? Assume a link can transmit 4 bytes per cycle.
C. (3 pts) If the network is designed to use cutthrough routing, what it is the minimum latency for sending a single packet from one processor to another? Assume a link can transmit 4 bytes per cycle.
Heterogeneous Parallelism
Problem 2. (9 points): 留学生代写assignment
You are part of a team that is designing new family of single-chip parallel processors.Your colleagues have already designed the following two CPUs, which will be the building blocks of your system design:
CPU-Lean: this CPU was designed for area efficiency;
CPU-Fast: this CPU was designed for speed. It is twice as fast as the CPU-Lean design, but it also takes up four times as much area.
Your team is considering several diferent machine designs, having an overall area equivalent to that of N CPU-Lean cores. That is, it will have Pr lean cores and Pr fat cores, such that 4Pr+ Pr = N.
Assume the following:
- The key benchmark that your team cares about takes 200 seconds to run sequentially on a single CPU-Lean core, and 100 seconds to run sequentially on a single CPU-Fast core.
- The benchmark’s computation consists of parallel and sequential parts, where the fraction of the orig-inal sequential time that is parallel is f. These two cannot overlap: while the sequential portion is executing on one core, the others remain idle.
- The parallel portion of the benchmark will experience linear speedup when it runs on multiple CPUs (i.e., there are no inefficiencies in running in parallel).
A. (1pt) First consider a lean-only machine, where Pr = 0. Write an equation for the total execution time of the benchmark, as a function of f and PL, making optimal use of the processing elements. 留学生代写assignment
B. (2pts) Now consider the case where Pr > 0 Write an equation for the total execution time of the benchmark, as a function of f, Pl, and Pr, making optimal use of the processing elements.
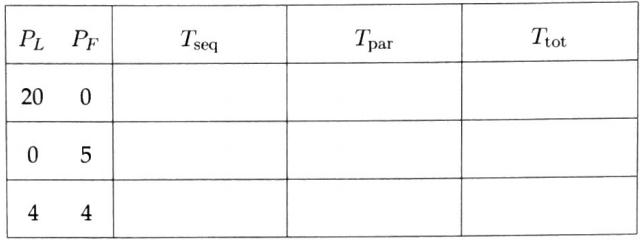
C. (6pts) Using your equations above, calculate the execution time (in seconds) for the benchmark with the following machine configurations (all with N = 20), assuming f = 0.90.
As an aid, separately list the time spent for the sequential portion Tseq, the time spent for the parallel portion Tpar, and the overall time Ttot = Tseq + Tpar.
Lock-Free Data Structures
Problem 3. (8 points):
Consider the following version of compare-and-swap:
bool CAS (int★addr, int check, int new) {
atomic {
int old = *addr; // Read
if (old == check) { // Compare
★addr = new; // Write
return true;
}
return false;
}
}
You are given the following sequential code implementing a bounded stack of integers using an array and a counter indicating the number of elements in the stack. 留学生代写assignment
#define MAXLEN 1000
int stack [MAXLEN] ;
int count = 0;
void push(int x) {
int ccount = count;
if (ccount >= MAXLEN)
return; // Silently fail if stack is full
stack [ccount] = x;
count = ccount + 1 ;
}
void pop (int→val) {
int ccount = count;
if (ccount == 0)
return; // Silently fail if stack is empty
*val = stack [ccount-1];
count = ccount - 1;
}
Here are attempts at lock- free implementations of push and pop:
void push(int x) {
while (1) {
int ccount = count;
if (ccount >= MAXLEN)
return; // Silently fail if stack is full
if (CAS (&count, ccount, ccount+1)) {
stack [ccount] = x;
return;
}
}
}
A. (4 pts) Identify a problem with the lock-free versions of push and pop.
B. (2 pts) Explain briefly why it is not possible to do lock-free implementations of these operatio using CAS. 留学生代写assignment
C. (2 pts) Suppose you have a double-word CAS with the following prototype:
// Atomic compare-and-swap two integers simultaneously
// Both locations are updated if and only if both exist ing
// Both locations are updated if and only if both exist ing
bool DCAS (int *addr1, int check1, int newl,
int *addr2, int check2, int new2) ;
Explain (without writing code) how you could implement the push operation using DCAS.
Memory Consistency

Problem 4. (10 points):
Assume that global variable data has initial value 0, and ready has initial value false. Consider following code snippets being executed concurrently by two threads:
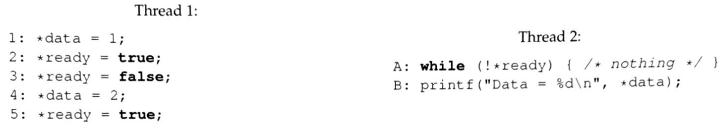
A. (6 pts) For sequentially consistent execution, indicate which of the fllowving outputs is possible.For each, give an ordering of the 7 steps (1-5 for Thread 1 and A-B for Thread 2) that would lead to this outcome. For the sequentially consistent cases, the ordering must be sequentially consistent.

B. (2 pts) Now suppose this code runs on a processor with a weak consistency model, where loads and stores to different memory locations by one thread can appear to occur to other threads as if they did not occur in program’ order. Would this change what the program could print? Explain your answer.
C. (2 pts) Where could you place a minimum set of fences to guarantee that only sequenially consistent outputs would occur with this program?
Transactions on Trees
Problem 5. (12 points):
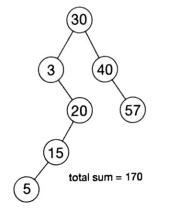
Consider the binary search tree ilustrated below.
The operations insert (insert value into tee, assuning no duplicates) and sum (retumn the sum of all elements in the tree) are implemented as transactional operations on the tree as shown below: 留学生代写assignment
struct Node {
Node *1eft, *right;
int value;
};
Node* root; // root of tree, assume non-null
void insertNode (Node* n,int value) {
if (value < n) {
if (n->left == NULL)
n->left = createNode (value) ;
} else {
if (n->right == NULL)
n->right = createNode (value) ;
else
insertNode (n->right, value) ;
}
}
int sumNode (Node* n) {
if (n = null) return 0;
int total = n->value;
total += sumNode (n->right) ;
total += sumNode (n->right) ;
return total;
}
void insert (int value) {
bool done = false;
while (!done) {
xbegin() ;
insertNode (root, value) ;
done = xend();
}
int sum() {
int rval = 0;
bool done = false; .
while (!done) {
xbegin() ;
rval = sumNode (root) ;
done = xend() ;
}
return rval;
}
Consider when the fllwing four operations are executed by dfferent threads, starting with the original tree.
T1: insert (10) ;
T2: insert (25) ;
T3: insert (24) ;
T4: printf(“Sum = d\n”, sum());
A. (4 pts) Consider the different orders in which these operations could be executed. Draw all possible trees that could result. (Note: you can draw just the subtrees rooted at node 20, since that is the only part of the tree that is affected.)
B. (2 pts) How many dfferent values could thread T4 print? Explain. (You need not list them,)
C. (2 pts) Do your answers to parts A or B change depending on whether the implementation of trans-actions uses optimistic or pessimistic conflict detection? Why or why not?
D. (2 pt)Consider an implementation using lazy data versioning and optimistic conlict detection that manages transactions at the granularity of tree nodes (the read and writes sets are lsts of nodes). AS-sume that the transaction for insert (10) commits when those for insert (24) and insert (25) are at node 20, and for sum() is at node 40. Which of the four transations (if any) are aborted?Please describe why.
E. (2 pts) Now consider a version that uses optimistic conflict detection for reads and pessimistic conlict detection for writes. Does transactional memory in this case offer any performance benefit for sum() compared to a fine grained locking approach? Explain.
A Simple lmage Processing Pipeline
Problem 6. (12 points): 留学生代写assignment
Consider the fllowving code to perform a vertical convolution on an input image.
float input [H+3] [W];
float output [H] [W];
void convolve (f1oat output[H][W], float input[H][W]) {
for (int j=0; j<H; j++) {
for (int i=0; i<W; i++) {
float accum = 0.f;
for (int jj=0; jj<4; jj++) {
1 count as two floating -point operations
accum += 0.25 * input [j+jj][i];
}
output[j][i] = accum;
}
}
}
convolve (output, input);
We consider execution under the following conditions:
- H=W = 4096.
- The cache is fully associate and uses write-back plus write-allocate policies. It has a capacity of 16384 bytes and a block size of 32 bytes.
- Both arrays begin on cache boundaries.
A. (2 pts) What is the arithmetic intensity of this program, defined as the number of floating point operations divided by the number of load and store operations.
B. (3 pts) Under the conditions described, what would be the cache hit rate for load operations? 留学生代写assignment
C. (3 pts) A colleague suggests switching the outer two loops, as follows:
void convolve (float output [H] [W],float input [H] [W]) {
for (int i=0; i<W; i++) {
for (int j=0; j<H; j++) {
float accum = 0.f;
for (int jj=0; jj<4; jj++) {
// count as two floating - point operations
accum += 0.25 + input [j+jj] [i];
}
output[j] [i] = accum;
}
}
}
What would be the hit rate for load operations in this case?
D. (4 pts) Describe (in words; no code is necessary) how you could modify the second version of the program to achieve the maximum possible hit rate on loads, while having the same arithmetic in-tensity? What would that hit rate be?

更多代写:留学生经济作业Econ Business代写 雅思代考靠谱吗 美国加拿大代考 美国金融Midterm代考 美国留学生代修网课 论文proposal模板
