Problem set
Microeconomics
Proof exercises for a production economy
生产经济代写 a. Show that the production functions are concave, strictly increasing and homogeneous of degree one for all j = 1, 2.
Problem 1 生产经济代写
Consider the 2 x 2 production model. Production functions are given by
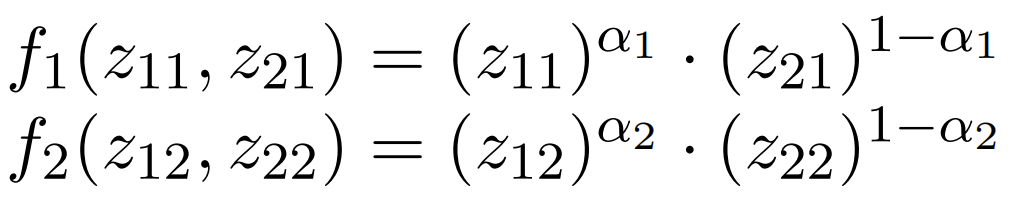
where αj∈ (0, 1) for all j = 1, 2 and zij ≥ 0 for all i = 1, 2 and j = 1, 2.
a. Show that the production functions are concave, strictly increasing and homogeneous of degree one for all j = 1, 2.
b. Show that if the set of technologically efficient factor allocations ever cuts the diagonal of the Edgeworth Box, then it must coincide with the diagonal.
c. Show that the factor intensity of one of the commodities exceeds that of the other at every point along the set of technologically efficient factor allocations, assuming that they do not cut the diagonal.
d. Show that any ray from either of the two origins of the box can intersect the set of technological effiffifficient factor allocations at most once. Use this result to show that the factor intensities of the two commodities and the MRTS change monotonically as you move along the Pareto set from the origin.
Problem 2 生产经济代写
Consider a pure exchange economy with two goods and two consumers, where consumers have the following utility functions
U1 = log(x11) + 2 log(x21)
U2 = 2 log(x12) + log(x22)
and endowment vectors ω1 = (9, 3) and ω2 = (12, 6).
a. Obtain the excess demand function for each good and verify that Walras’ Law holds.
b. Find the equilibrium price ratio.
c. What is the Walrasian equilibrium allocation?
d. Given initial endowments do not change, derive the equation for the Pareto set.
Problem 3 生产经济代写
Robinson was a lonely man living on an island all by himself. Out of boredom, he established a company, called M&M’s (Monopoly Mango’s). To amuse himself, he would either eat mangos that he himself produces or would enjoy the sandy beaches doing nothing. His amusement is measured by his utility function
u(m, l) = m1/2 l1/2
where m is his mango consumption and l is the time he spends on the beach. His company’s production function is given by
f(x) = x1/2
where x is Robinson’s labour input and y = f(x) is his company’s mango output. Robinson is the Warren Bu↵et of his island, he had no mango’s to start with! And to further simplify things, he considers his total time, which he would allocate between the beach and the work, as one unit. Now to close his life (our model) lets assume the price of mangos, p, and the price of his labour, w, are set exogenously and hence taken as given by Robinson.
a. Find Robinson’s demand for mangos and beach time
b. Find M&M’s demand for Robinson’s labour.
c. Obtain Walrasian equilibrium allocations, prices and profits.
d. Show the equilibrium regarding Robinson’s life ( our model) using an Edgeworth Box Diagram.

更多代写:计算机专业作业代写 Online exam代考推荐 英国ESSAY代写 转学ESSAY代写 Reflection paper 代写 开放经济代写
