理科计算机代写 统计作业代写

Homework 7

理科计算机代写 Under the conditions stated in (a), the model fitted 1) will not be regulated, 2) the two loss function will be identical.

Problem 1 理科计算机代写

(a)

The value of 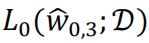 will no higher than  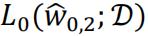as the extra polynomial term with  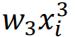can fit better to the truth value. At worst case  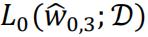can achieve the same lowest value as  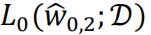does by setting the first 3 w entries the same and leave w₃ as zero.

(b)

If λ=0, then as we discussed in part (a) the loss value with higher terms will be no lower than ones with lower terms. Therefore we will always have 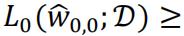 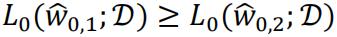regardless the true underlying model. So this is a poor criterion as it will always lead to the choice of  .

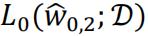(c)

With cross validation, models overfitted to some subset of data will fail to generalize to the rest data. Therefore using CV, we may find that a model with higher complexity will perform worse than a model with lower complexity because the added complexity is prone to overfitting.

(d)

As  increase from 0, the model fitted will tend to choose smaller value for w to minimize the penalty. Under cross validation, we may find that final model chosen will have a different D value than previous ones. This is because that models fit now with a positive  will be regulated from overfitting. And it’s possible that a higher D value model can balance better between overfitting and underfitting.

Question 2  理科计算机代写

(a)

To let 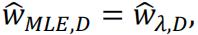, we must have λ=0 so the model fitted will not be biased. The distribution of random variables  must be symmetric around zero.

(b)

Under the conditions stated in (a), the model fitted 1) will not be regulated, 2) the two loss function will be identical. Therefore they will return the same set of parameters.

(c)

D controls the complexity of the model. A higher D value will allow the fitted polynomial to go higher order, and thus can fit the data points better. However this “fitting” may be overfitting to the training set, and the generalization of the model will be poor. Thus a higher D value will contribute to lower bias, but also to higher variance.

λ affects how varied the parameter is allowed to be, a high  value will encourage the model fitted to have smaller values for w. This will lead to a model underfitting the trainning set, however will also help avoiding overfitting. Thus a higher  value will contribute to higher bias, but also to lower variance.

Question 3

(a)

Since the outcome is binary, we can use the MSE loss function which is to be minimized:

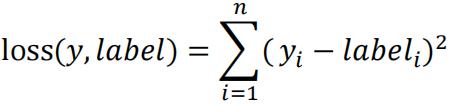
where label is the true label, and y is the predicted label associated with the M cuts and labels. The value of this loss function will be minimized when y_i =𝑙𝑎𝑏𝑒l_i for all i.

Given a set of cuts and labels, we will first loop through all value  and generate the associated  for each data point. Then we will use the formula above to calculate the loss function.

(b)

The benefit of using a large M is that we can set up very small intervals to fit each data point. The extreme case is that each data point will have an interval of its own with the correct label.

The risk with large M is that we will overfit the data and the model will not generalize well to actual application.

(c)

I will use a penalty term in my loss function, and use cross validation to find the best value for λ.

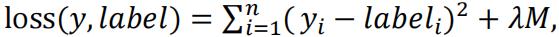
1.The new loss function will be: , therefore when the M is large it gets penalized.

2.Now we will use a 10 fold cross validation to find the best value for λ:

• We will decide a candidate list of possible λ values.
• For each value, we will use a 10 fold cross validation to find the average loss value.
• We will then find the value that has the lowest average loss value.

Use the found  value, fit the model again with all of the data.

Question 4

Using conditional probability:

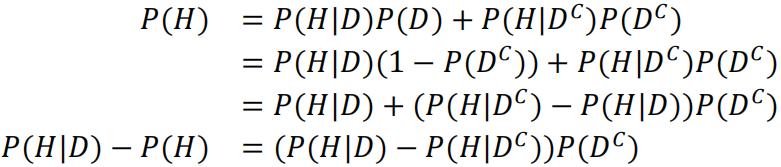
Since we are told P(H|D)>P(H), we can write P(H)=h, and P(H|D)=h+Δh for simplicity:

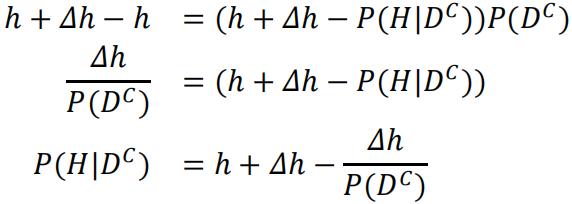
And that P(D^C)<1 because if not then P(H|D^C)and P(H|D)=0 and P(H)>P(H|D). So we can conclude:

P(H|D^C)<P(H)

Question 5  理科计算机代写

(a)  

The probability density function for each data point y_i is: 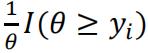 given the uniform distribution. Thus the likelihood function is:

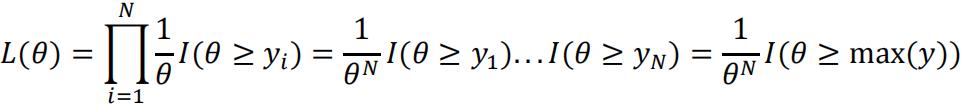
(b)

Since θ>0 and 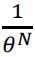 decreases with θ, the function is maximized when θ=max(y₁,…,y_N).

(c)

Proof:

With the given Pareto distribution prior:

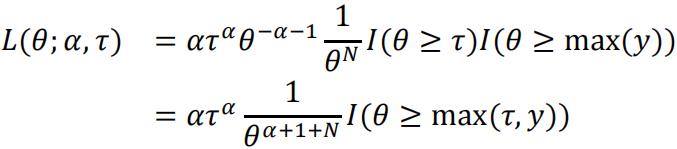
Now we can see that the Pareto distribution prior is conjugate to the likelihood function. And the new MLE given α₀,τ₀is max(τ,y₁,…,y_N).