MT3505 Algebra: Rings & Fields
环与域代写 1.For each set in Q15 of the Chapter 1 Tutorial Sheet, determine whether or not it is an ideal of the given ring. Show all working.
1.
For each set in Q15 of the Chapter 1 Tutorial Sheet, determine whether or not it is an ideal of the given ring. Show all working. An ideal of a ring is a special kind of subring. So, if a subset of a ring is not a subring, it cannot be an ideal.
(i) the positive integers in Z;
(ii) all polynomials with integer constant in Q[x];
(iii) all polynomials of degree at least 6 in Q[x];
(iv) the set of polynomials a0 + a1x + a2x2 + · · · + anxn in R[x] for which a0 = a1 = 0
2. 环与域代写
We have seen that the centre C(R) of a ring R is always a subring of R. Is C(R) necessarily an ideal of R? Give a proof or counterexample.
3.
Let R be the set of matrices
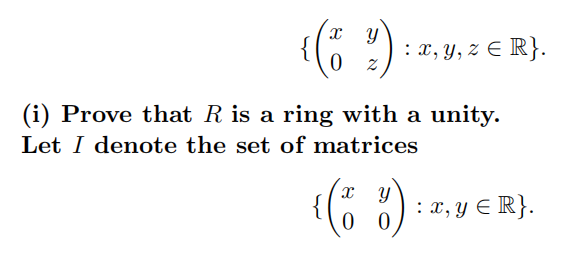
(ii) Show that I is an ideal of R.
(iii) Show that I is not an ideal of M2(R).
4.
Let I be an ideal in a ring R. Prove that I[x] is an ideal in R[x].
5. 环与域代写
Let I and J be ideals in a commutative ring R.
(i) Prove that
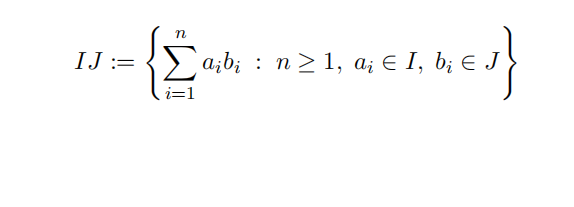
is an ideal in R.
(ii) Prove that IJ ⊆ I ∩ J.
(iii) Use (ii) to prove that if R is an integral domain and I, J are ideals of R neither of which is {0}, then I ∩ J ≠ {0}. Is this true when R is not a domain?
(iv) Find examples of ideals I and J such that IJ ≠ I ∩ J.
(v) Is {ij : i ∈ I, j ∈ J} an ideal?
6. 环与域代写
(i) If R is a nontrivial commutative ring with identity whose only ideals are {0} and R, prove that R is a field.
(ii) If R is a nontrivial commutative ring with identity, do the non-invertible elements of R form an ideal? Prove this or find a counterexample.

更多代写:计算机网上Quiz代考 托福代考 英国统计学online exam代考 微观经济学essay代写 台湾留学生英语论文代写 网课代管
