PHYSICS 1
5 Questions
物理1代写 Identical blocks 1 and 2 are placed on a horizontal surface at points A and E, respectively, as shown. The surface is frictionless except for the ···
Directions: Questions 1, 4, and 5 are short free-response questions that require about 13 minutes each to answer and are worth 7 points each. Questions 2 and 3 are long free-response questions that require about 25 minutes each to answer and are worth 12 points each. Show your work for each part in the space provided after that part.
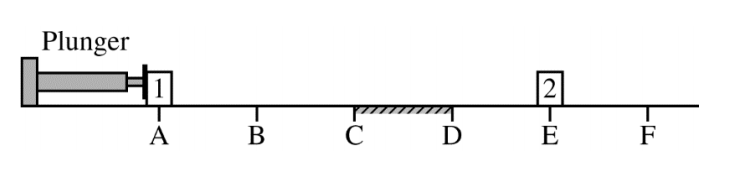
1.(7 points, suggested time 13 minutes)
Identical blocks 1 and 2 are placed on a horizontal surface at points A and E, respectively, as shown. The surface is frictionless except for the region between points C and D, where the surface is rough. Beginning at time t A , block 1 is pushed with a constant horizontal force from point A to point B by a mechanical plunger. Upon reaching point B, block 1 loses contact with the plunger and continues moving to the right along the horizontal surface toward block 2. Block 1 collides with and sticks to block 2 at point E, after which the two-block system continues moving across the surface, eventually passing point F.
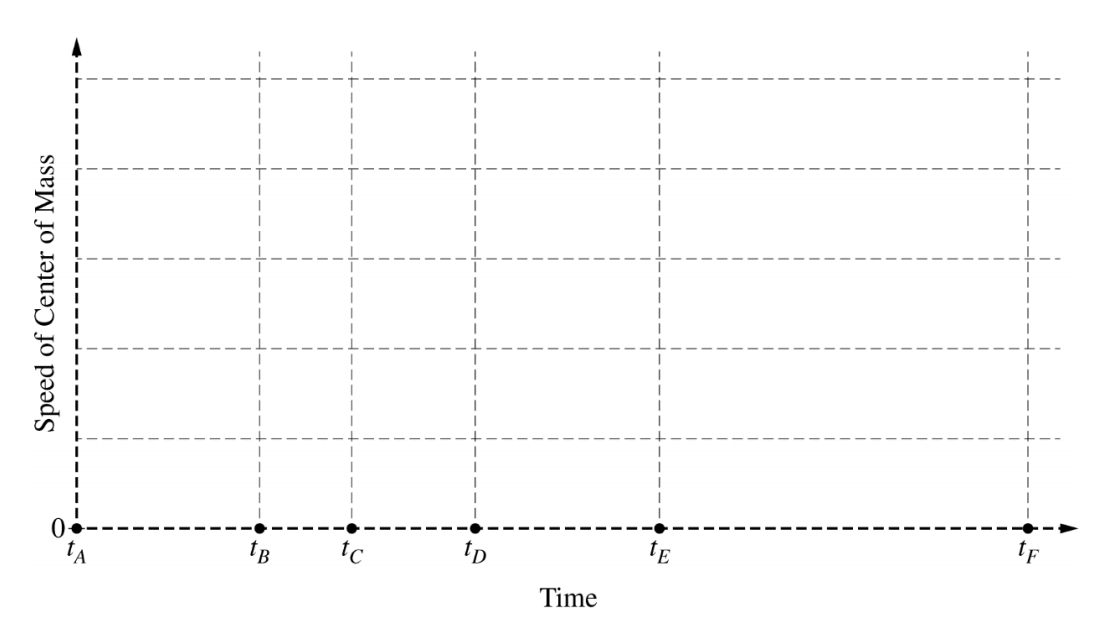
(a) On the axes below, sketch the speed of the center of mass of the two-block system as a function of time, from time t A until the blocks pass point F at time t F . The times at which block 1 reaches points A through F are indicated on the time axis.
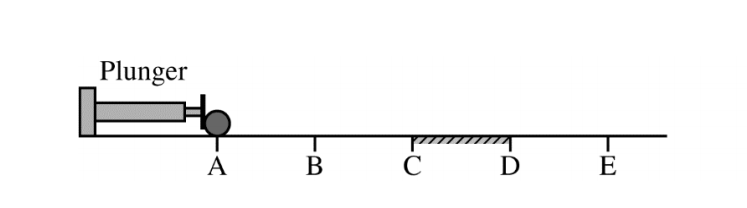
(b) The plunger is returned to its original position, and both blocks are removed. A uniform solid sphere is placed at point A, as shown. The sphere is pushed by the plunger from point A to point B with a constant horizontal force that is directed toward the sphere’s center of mass. The sphere loses contact with the plunger at point B and continues moving across the horizontal surface toward point E. In which interval(s), if any, does the sphere’s angular momentum about its center of mass change? Check all that apply.
____ A to B ____ B to C ____ C to D ____ D to E
_____ None
Briefly explain your reasoning.
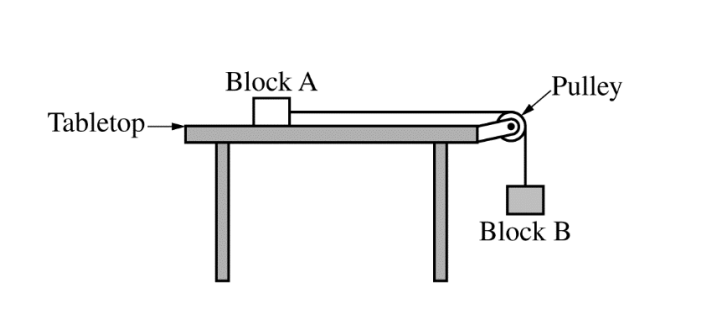
2.(12 points, suggested time 25 minutes) 物理1代写
This problem explores how the relative masses of two blocks affect the acceleration of the blocks. Block A, of mass mA, rests on a horizontal tabletop. There is negligible friction between block A and the tabletop. Block B, of mass mB , hangs from a light string that runs over a pulley and attaches to block A, as shown above. The pulley has negligible mass and spins with negligible friction about its axle. The blocks are released from rest.
(a)
i. Suppose the mass of block A is much greater than the mass of block B. Estimate the magnitude of the acceleration of the blocks after release.
Briefly explain your reasoning without deriving or using equations.
ii. Now suppose the mass of block A is much less than the mass of block B. Estimate the magnitude of the acceleration of the blocks after release.
Briefly explain your reasoning without deriving or using equations.
(b)
Now suppose neither block’s mass is much greater than the other, but that they are not necessarily equal. The dots below represent block A and block B, as indicated by the labels. On each dot, draw and label the forces (not components) exerted on that block after release. Represent each force by a distinct arrow starting on, and pointing away from, the dot.

(c)
Derive an equation for the acceleration of the blocks after release in terms of mA , mB , and physical constants, as appropriate. If you need to draw anything other than what you have shown in part (b) to assist in your solution, use the space below. Do NOT add anything to the figure in part (b).
(d)
Consider the scenario from part (a)(ii), where the mass of block A is much less than the mass of block B. Does your equation for the acceleration of the blocks from part (c) agree with your reasoning in part (a)(ii) ?
____ Yes ____ No
Briefly explain your reasoning by addressing why, according to your equation, the acceleration becomes (or approaches) a certain value when mA is much less than mB .
(e)
While the blocks are accelerating, the tension in the vertical portion of the string is T1 . Next, the pulley of negligible mass is replaced with a second pulley whose mass is not negligible. When the blocks are accelerating in this scenario, the tension in the vertical portion of the string is T2 . How do the two tensionscompare to each other?
____ T2 > T1 ____ T2 = T1 ____ T2 < T1
Briefly explain your reasoning.
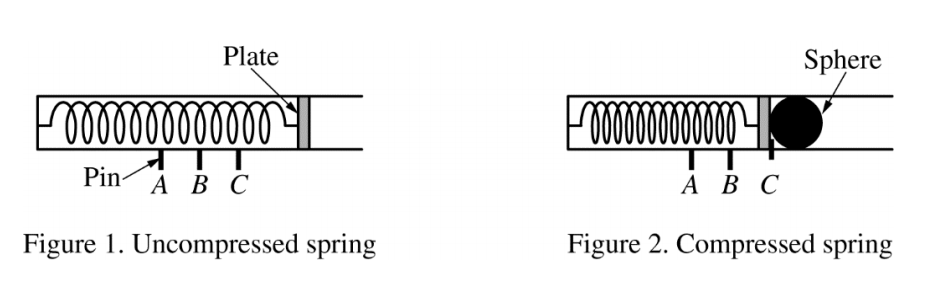
3.(12 points, suggested time 25 minutes) 物理1代写
A projectile launcher consists of a spring with an attached plate, as shown in Figure 1. When the spring is compressed, the plate can be held in place by a pin at any of three positions A, B, or C. For example, Figure 2 shows a steel sphere placed against the plate, which is held in place by a pin at position C. The sphere is launched upon release of the pin.
A student hypothesizes that the spring constant of the spring inside the launcher has the same value for different compression distances.
(a)
The student plans to test the hypothesis by launching the sphere using the launcher.
i. State a basic physics principle or law the student could use in designing an experiment to test the hypothesis.
ii. Using the principle or law stated in part (a)(i), determine an expression for the spring constant in terms of quantities that can be obtained from measurements made with equipment usually found in a school physics laboratory.
(b)
Design an experimental procedure to test the hypothesis in which the student uses the launcher to launch the sphere. Assume equipment usually found in a school physics laboratory is available. In the table below, list the quantities and associated symbols that would be measured in your experiment. Also list the equipment that would be used to measure each quantity. You do not need to fill in every row. If you need additional rows, you may add them to the space just below the table.
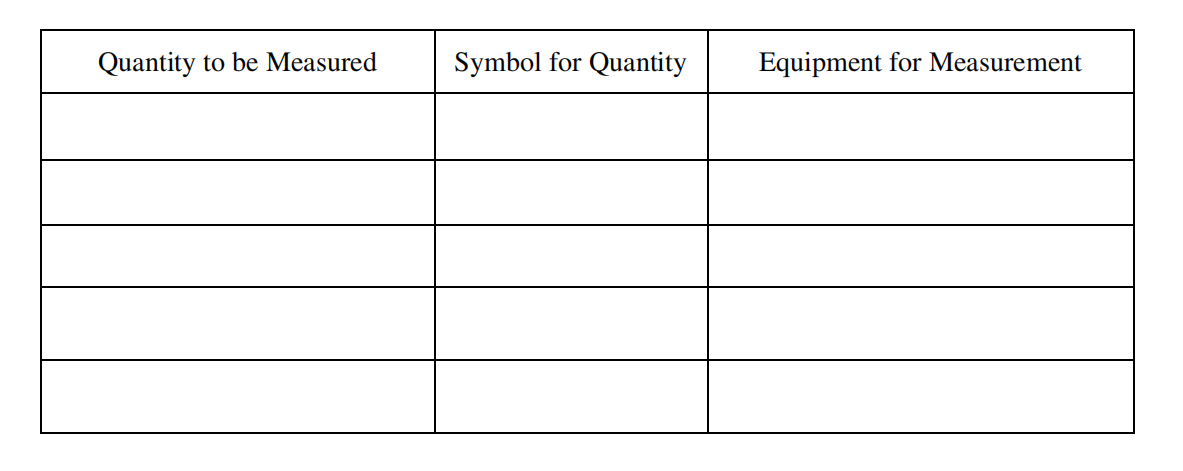
Describe the overall procedure to be used to test the hypothesis that the spring constant of the spring inside the launcher has the same value for different compression distances, referring to the table. Provide enough detail so that another student could replicate the experiment, including any steps necessary to reduce experimental uncertainty. As needed, use the symbols defined in the table and/or include a simple diagram of the setup.
(c)
Describe how the experimental data could be analyzed to confirm or disconfirm the hypothesis that the spring constant of the spring inside the launcher has the same value for different compression distances.
(d)
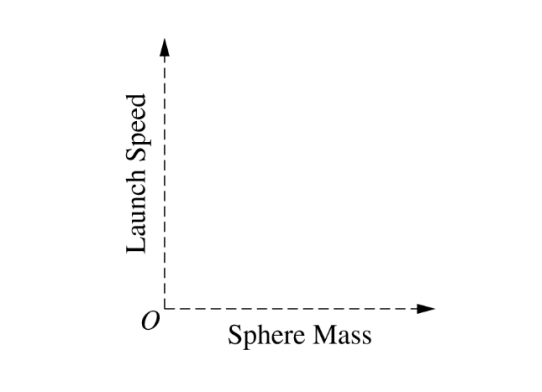
Another student uses the launcher to consecutively launch several spheres that have the same diameter but different masses, one after another. Each sphere is launched from position A. Consider each sphere’s launch speed, which is the speed of the sphere at the instant it loses contact with the plate. On the axes below, sketch a graph of launch speed as a function of sphere mass.
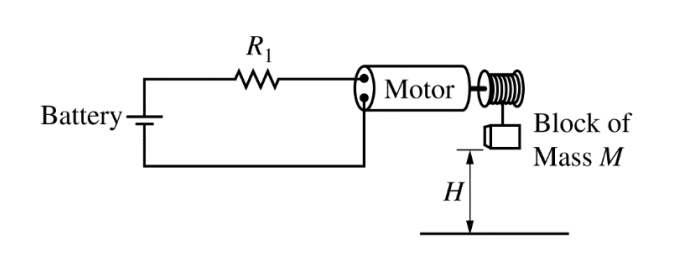
4.(7 points, suggested time 13 minutes) 物理1代写
A motor is a device that when connected to a battery converts electrical energy into mechanical energy. The motor shown above is used to lift a block of mass M at constant speed from the ground to a height H above the ground in a time interval Δt. The motor has constant resistance and is connected in series with a resistor of resistance R1 and a battery.
Mechanical power, the rate at which mechanical work is done on the block, increases if the potential difference (voltage drop) between the two terminals of the motor increases.
(a) Determine an expression for the mechanical power in terms of M, H, Δt, and physical constants, as appropriate.
(b) Without M or H being changed, the time interval Dt can be decreased by adding one resistor of resistance R2 , where R2 > R1, to the circuit shown above. How should the resistor of resistance R2 be added to the circuit to decrease Δt ?
___ In parallel with the battery
___ In parallel with R1
___ In parallel with the motor
___ In series with the battery, R1 , and the motor
In a clear, coherent, paragraph-length response that may also contain figures and/or equations, justify why your selection would decrease Δt.
5.(7 points, suggested time 13 minutes) 物理1代写
A tuning fork vibrating at 512 Hz is held near one end of a tube of length L that is open at both ends, as shown above. The column of air in the tube resonates at its fundamental frequency. The speed of sound in air is 340 m/s.
(a) Calculate the length L of the tube.
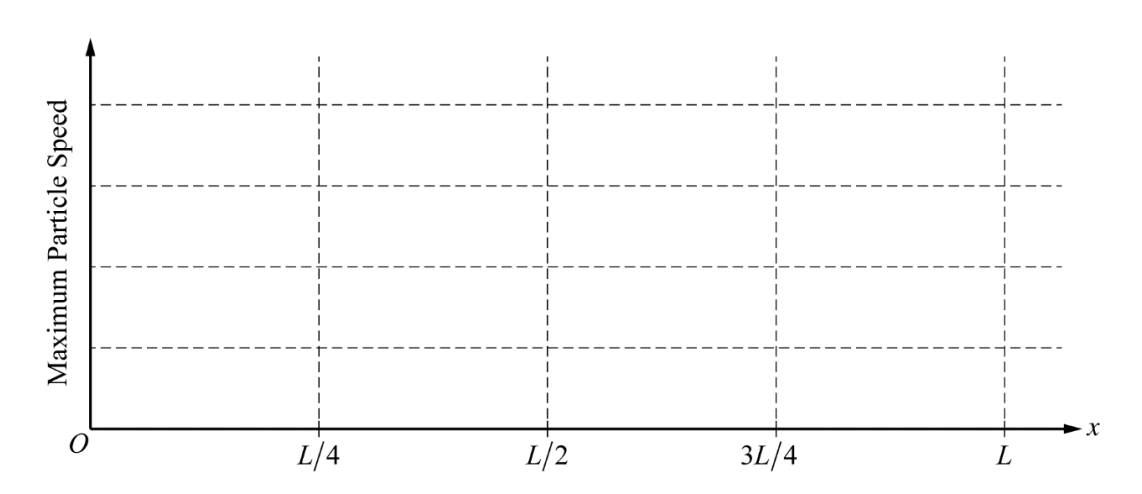
(b) The column of air in the tube is still resonating at its fundamental frequency. On the axes below, sketch a graph of the maximum speed of air molecules as they oscillate in the tube, as a function of position x, from x = 0 (left end of tube) to x = L (right end of tube). (Ignore random thermal motion of the air molecules.)
(c) The right end of the tube is now capped shut, and the tube is placed in a chamber that is filled with another gas in which the speed of sound is 1005 m/s. Calculate the new fundamental frequency of the tube.

其他代写:program代写 project代写 assignment代写 加拿大代写 python代写 report代写 paper代写 essay作业代写 作业代写 北美作业代写 java代写 matlab代写 finance代写 英国代写 homework代写
