Physics代写 orbit program代写 differential equations代写 code代写

Physics 307 Homework 6

Physics代写 In this homework assignment, you will use your orbit program to simulate a highly elliptical orbits, and then a binary star.

Due Thursday, 25 October, at 5 PM

In this homework assignment, Physics代写

you will use your orbit program to simulate a highly elliptical orbits, and then a binary star.

1. Considera highly elliptical orbit such as a  At aphelion, Halley’s comet is 35.1 AU from the Sun and has a velocity of 0.193 AU/year. Use your program to simulate the orbit of Halley’s comet. How close does it come to the Sun at perihelion, and how fast is it traveling there?Physics代写

About how many timesteps are required to simulate this orbit reasonably accurately? Compare this to the value for a circular orbit that you determined

2. Extracredit: Can you think of any way to mitigate this and simulate the orbit with fewer timesteps? Implement

last week. What makes cometary orbits so much harder to simulate accurately?

3. If you’re not familiar with Kepler’s laws of orbital motion, look them up. Does the behaviorof your simulation reflect Kepler’s second law (qualitatively; you do not need to measure areas!)Physics代写
4. Now,modify your program to simulate a binary star system with two stars of unequal mass– that is, two objects responding to each other’s

Hints: Physics代写

• Ifyou measure mass in solar masses, G still has a value of 4π².
• Youwill now need to use

  

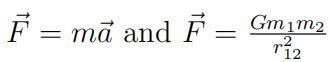
  together to find the accelera-tions.

• Your count of dynamical variables has now doubled toeight:

x₁, y₁, v_x1 , v_y1 for the firststar

x₂, y₂, v_x2 , v_y2 for the secondstar

• Theleapfrog prescription is still the same:

(a)Evolve the position variables (all four of them!) forward bydt/2

(b)Evolve the velocity variables (all four of them!) forward by dt (this is the hardpart)

(c)Evolve the position variables forward by dt/2again Physics代写

Your cut-and-paste skills will come in handy here, as you will be typing multiple copies of very similar code. But be careful of editing errors when doing this!

• The radius vector that appears in the differential equations is now the separation vector between the two stars. The origin no longer plays any special role in the dynamics.
• Since the x and y that appear explicitly in the differential equations comefrom the components of rˆ₁₂, they will become x₁ − x₂, Physics代写

5. Important: if you don’t want your simulation to “drift” out of the viewport, thenyou will want to ensure that the total momentum is  See the end of this document for how to do this.

Run your simulation, and monitor conservation of total energy to ensure that it is behaving properly. You now can’t compute energy per unit mass, since you have two masses; the total energy will be

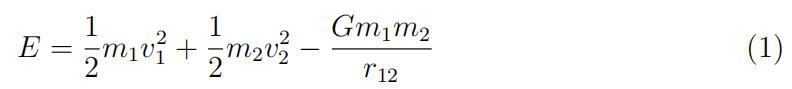
6. Now,finally, modify your code to simulate the gravitational interactions of three  This is no more complicated than two; you just have some copy-paste work to do, since each object now feels the force from two neighbors, rather than just one.

Play around with what you can create – make things move in three dimensions, etc. Note that if two bodies get too close together, they will experience a very large force that is probably too big for your timestep to accurately simulate. Can you make a stable sun-planet-moon system?Physics代写

Avoiding solar system drift

The total momentum of a system of two stars is

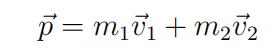
This gives a center-of-mass velocity of

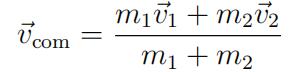
By calculating this value and subtracting it from each of your objects’ initial velocities, you ensure that the total center-of-mass velocity (and thus the total momentum) is zero, and your simulation won’t drift. This can be done with code like the following:

double vxc,vyc; //center-of-mass velocities vxc = (m1*vx1 + m2*vx2) / (m1+m2);

vyc = (m1*vy1 + m2*vy2) / (m1+m2); vx1 = vx1 – vxc;

vy1 = vy1 – vyc; vx2 = vx2 – vxc; vy2 = vy2 –  vyc;

更多其他：C++代写 r代写 代码代写  考试助攻 C语言代写 finance代写 lab代写 计算机代写 code代写 data代写 report代写 代写CS matlab代写 project代写 物理代写 program代写

合作平台：天才代写 幽灵代写 写手招聘 Essay代写