MATH 487/587
Fall 2021
澳洲MATH数学代考 3(20pt). Let R4 be equipped with the Minkowski metric. The Hodge star operator y is a linear transformation on the space of 2-forms ∧2(R4).
Name: ID:
Note: Show steps for your work.
1(20pt) Prove Einstein’s energy-mass equation E = mc2, where c is the speed of light in vacuum. 澳洲MATH数学代考
2(20pt). Let R be a rectangle in the (s, t)-plane. Derive the Euler-Lagrange equation for the function x(s, t) that minimizes the integral
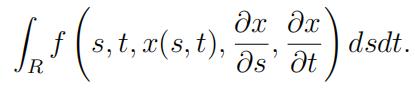
3(20pt). Let R4 be equipped with the Minkowski metric. The Hodge star operator y is a linear transformation on the space of 2-forms ∧2(R4). 澳洲MATH数学代考
(a)Show that y2= −1 on ∧2.
(b)Inview of (a), y has eigenvalues i and −i with corresponding eigenspaces denoted by E+ and E−, 2-forms in E+ are call self-dual forms, and that in E− are called anti-self dual forms. Determine E+ and E−.

4(20pt). Given vector fields E = (E1, E2, E3) and E = (E1, E2, E3), we let F be the associated Faraday 2-form. 澳洲MATH数学代考
(a)Showthat the Maxwell’s equations can be written as
dF = 0, y d y F = J,
where J is the current 1-form.
(b)Show that if F is self-dual or anti-self-daul then y d y F = 0, i.e., F satisfies the Maxwell’s equations in vacuum. 澳洲MATH数学代考
5(20pt). The electromagnetic Lagrangian is
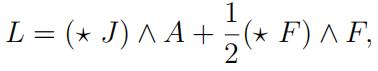
where F is the Faraday 2-form, A is the potential 1-form and J is the current 1-form. Prove Proposition 11.4.1 in the textbook.

更多代写:Matlab代写价格 澳洲Midterm代考 北美MBAEssay代写 北美report代写 Research Paper作业代写 实证金融项目代写
