澳大利亚数学代考 Test代写

Test 4, March 27, 2020

MAT235Y1Y

Duration: 24 hours

澳大利亚数学代考 a)(3 marks) Evaluate the line integral C sin x dy, where C is the part of the curve y = x2 from the point (0, 0) to the point (π, π2).

This test has 6 pages. 澳大利亚数学代考

Total: 50 marks

All answers must be your own work.

No marks will be given for a completely wrong solution.  

Last name . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

First name  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Student ID number . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Email  . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1. (10 marks)  澳大利亚数学代考

a)(3 marks) Evaluate the line integral C sin x dy, where C is the part of the curve y = x² from the point (0, 0) to the point (π, π²).

(A) 2π   (B) π   (C) 0    (D) −π (E) ^π

Write the (capital) letter of the answer in this box. Only the answer in the box will be marked. )

b)(4 marks) Evaluate the line integral C F n ds, where C is the circle x²+ y² = 4 with counter clockwise orientation, n is the unit outward normal vector to the curve C and F(x, y) = (x3 , ^2y3 ).  澳大利亚数学代考

(A) 6π   (B) 12π   (C) 0    (D) π   (E) 4

Write the (capital) letter of the answer in this box. Only the answer in the box will be marked. )

c)(3ma√rks) Set up the volume of the solid bounded by the surface x = 1 − z, the planes x = 0, y = 0, y = 1 and z = 0 as an iterated integral in the order of dy dx dz.

Answer                              

2.(10marks) Let F(x, y, z) = (yz, xz, xy).  澳大利亚数学代考

(a)(4marks) Show that curl F(x, y, z) = 0.

b)(6marks) Use a potential function f of F to solve the line integral ∫ F · dr, where C  is the curve given by ˙r(t) = (e^t, t² − 1, 2t + 1) from t = 0 to t = 1.

3.(10marks) Use transformations x+y = u, y = v to evaluate the inte-gral ∫∫ √4 − (x + y)2 dA, where D is the trapezoidal region bounded by the lines x + y = 1, x + y = 2, y = 0 and x = 0.  澳大利亚数学代考

4. (10marks) Evaluate the integral (x² +z) dV , where E is the solid E that lies within the cylinder x² +y² = 1 and the sphere x² +y² +z² = 4, and above the xy-plane.

5.(10 marks) Evaluate the integral 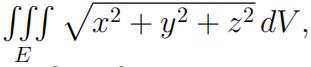 , where E is the solid bounded by the sphere x² + y² + z² = 4 and above the plane z = 1.

 

更多代写：Matlab网课代做  Online exma代写  英国Conclusion代写  爱尔兰paper代写  英国paper代写  数学Final exam代考

合作平台：essay代写 论文代写 写手招聘 英国留学生代写