当前位置：天才代写 > 数学代写代考,北美/加拿大/英国靠谱的数学作业代写机构 > 概率论Exam代写 MATH 233代写

概率论Exam代写 MATH 233代写

2021-11-11 15:36 星期四 所属： 数学代写代考,北美/加拿大/英国靠谱的数学作业代写机构 浏览：885

概率论Exam代写

Fall 2020 MATH 233

Exam 2

Theory of Probability

Wednesday November 11, 2020 2:00pm – 3:15pm

概率论Exam代写 Nationwide, the Math SAT exam has an average score of 500 (out of 800) and a standard deviationof 120 (assuming a normal distribution).

Your answer to each question (or sub-question), should be contiguous as you will have to clearly mark where your answer is when submitting to Gradescope.

  • No collaboration allowed.
  • Nooutside sources allowed (no notes, no books, etc.).
  • Only scientific calculators are allowed.
  • Tablesof the standard normal PDF and CDF are included.
  • Nocredit will be given without showing ALL work.
  • Pleaseplace a box around your answer for each question.

A scanned PDF must be uploaded to Gradescope by 3:25pm. No late submissions will be accepted.

Useful Random Variables  概率论Exam代写

  • Binomial(n,p) distribution, k = 0, . . . , n

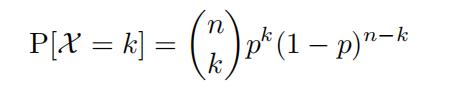(1)

 

  • Poisson(λ)distribution, k = 0, . . . , n
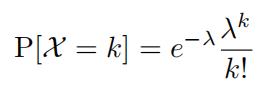
概率论Exam代写
概率论Exam代写

(2)

  • Gamma(α,λ) distribution, x > 0

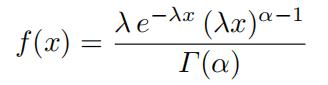(3)

  • Standardnormal distribution, −∞ < x < ∞
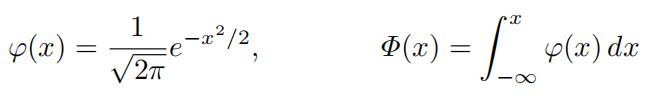
概率论Exam代写
概率论Exam代写

(4) 

  • Exponential(λ)distribution, x > 0

 (5)

1.Nationwide, the Math SAT exam has an average score of 500 (out of 800) and a standard deviationof 120 (assuming a normal distribution).

概率论Exam代写

(a)[ 5 points ] If five students who took the exam are selected at random, what is the probabilitythat exactly two of them scored at least 680?

(b)[ 5 points ] What is the probability that a randomly chosen senior scored less than400?

2.[ 5 points ] An insurance company insures 3000 people, each of whom will be in an accident with probability 0.001. Approximate the probability that the insurance company will have to payout on at most 2 accidents.  概率论Exam代写

3.[ 5 points ] The median of a random variable X is the value x such that P[X ≤ x] = 0. Compute the median of X ∼Exponential(3).

概率论Exam代写
概率论Exam代写

4.[ 10 points ] The mode of a continuous random variable is the value x which maximizes f (x), where f is the probability density function of . Find the mode of a Gamma(4.5, 0.5) random variable.

5.Considerthe discrete random variable X with probability mass function P[X = n] = C 3−|n|, for n = . . . , −2, −1, 0, 1, 2, . . ..

(a)[ 3 points ] Find C.  概率论Exam代写

(b)[ 3 points ] ComputeE[X ].

(c)[ 4 points ] What is P[X 2 = k] for k= 0, 1, 2, . . .?

  1. Considerthe discrete random variable X defined by its probability mass function:

P[X = 0] = 0.20,        P[X = 2] = 0.10,

P[X = 1] = 0.20,         P[X = 3] = 0.50.  (6)

(a)[ 5 points ] What is the expected value, µ, of X?

(b)[ 5 points ] What is the variance, σ2, of X?

7.[ 10 points ] Let X ∼ Binomial(123, 0.40). Use the normal approximation to the binomial distribution to estimate P[X= 42].   概率论Exam代写

8.[ 5 points ] Let Z be a standard normal random variable, with PDF denoted by ϕ and CDF denoted by Φ. Let X = Φ(Z). How is Xdistributed?

9.[ 5 points ] Let the random variable X ∼ Exponential(λ). Compute the probability density function of Y = F (X ), where F is the CDF ofX .

10.Let the random variable Z ∼ N (0,1).

(a)[ 7 points ] Compute the probability density function of Y =Z2.

(b)[  3  points] What kind of random variable is ? (Hint: Look at the PDFs on the first page of the exam. )

11.Considerthe continuous random variable X with density function f (x) = Cxe−2x for x ≥ 0. 概率论Exam代写

(a)[ 3 points] What is C?

(b)[ 3 points ] Find the distribution function F.

(c)[ 4 points ] What is P[X ≥1]?

12.[ 10 points ] Let X ∼ Exponential(λ), and Y = log X (i.e. the natural logarithm of X ). What isthe probability density function for Y?

Standard normal PDF
Decimal part \ Integer part 0 1 2 3 4
0.00 0.398942 0.241971 0.053991 0.004432 0.000134
0.02 0.398862 0.237132 0.051864 0.004173 0.000124
0.04 0.398623 0.232297 0.049800 0.003928 0.000114
0.06 0.398225 0.227470 0.047800 0.003695 0.000105
0.08 0.397668 0.222653 0.045861 0.003475 0.000097
0.10 0.396953 0.217852 0.043984 0.003267 0.000089
0.12 0.396080 0.213069 0.042166 0.003070 0.000082
0.14 0.395052 0.208308 0.040408 0.002884 0.000076
0.16 0.393868 0.203571 0.038707 0.002707 0.000070
0.18 概率论Exam代写 0.392531 0.198863 0.037063 0.002541 0.000064
0.20 0.391043 0.194186 0.035475 0.002384 0.000059
0.22 0.389404 0.189543 0.033941 0.002236 0.000054
0.24 0.387617 0.184937 0.032460 0.002096 0.000050
0.26 0.385683 0.180371 0.031032 0.001964 0.000046
0.28 0.383606 0.175847 0.029655 0.001840 0.000042
0.30 0.381388 0.171369 0.028327 0.001723 0.000039
0.32 0.379031 0.166937 0.027048 0.001612 0.000035
0.34 0.376537 0.162555 0.025817 0.001508 0.000032
0.36  概率论Exam代写 0.373911 0.158225 0.024631 0.001411 0.000030
0.38 0.371154 0.153948 0.023491 0.001319 0.000027
0.40 0.368270 0.149727 0.022395 0.001232 0.000025
0.42 0.365263 0.145564 0.021341 0.001151 0.000023
0.44 0.362135 0.141460 0.020328 0.001075 0.000021
0.46 0.358890 0.137417 0.019356 0.001003 0.000019
0.48 0.355533 0.133435 0.018423 0.000936 0.000017
0.50 0.352065 0.129518 0.017528 0.000873 0.000016
0.52 0.348493 0.125665 0.016670 0.000814 0.000015
0.54 0.344818 0.121878 0.015848 0.000758 0.000013
0.56 0.341046 0.118157 0.015060 0.000706 0.000012
0.58 0.337180 0.114505 0.014305 0.000657 0.000011
0.60 0.333225 0.110921 0.013583 0.000612 0.000010
0.62 0.329184 0.107406
0.012892
 0.000569 0.000009
0.64 0.325062 0.103961 0.012232 0.000529 0.000008
0.66 0.320864 0.100586 0.011600 0.000492 0.000008
0.68  概率论Exam代写 0.316593 0.097282 0.010997 0.000457 0.000007
0.70 0.312254 0.094049 0.010421 0.000425 0.000006
0.72 0.307851 0.090887 0.009871 0.000394 0.000006
0.74 0.303389 0.087796 0.009347 0.000366 0.000005
0.76 0.298872 0.084776 0.008846 0.000340 0.000005
0.78 0.294305 0.081828 0.008370 0.000315 0.000004
0.80 0.289692 0.078950 0.007915 0.000292 0.000004
0.82 0.285036 0.076143 0.007483 0.000271 0.000004
0.84 0.280344 0.073407 0.007071 0.000251 0.000003
0.86  概率论Exam代写 0.275618 0.070740 0.006679 0.000232 0.000003
0.88 0.270864 0.068144 0.006307 0.000215 0.000003
0.90 0.266085 0.065616 0.005953 0.000199 0.000002
0.92 0.261286 0.063157 0.005616 0.000184 0.000002
0.94 0.256471 0.060765 0.005296 0.000170 0.000002
0.96 0.251644 0.058441 0.004993 0.000157 0.000002
0.98 0.246809 0.056183 0.004705 0.000145 0.000002
Standard normal CDF
Decimal part \ Integer part 0 1 2 3 4
0.00 0.500000 0.841345 0.977250 0.998650 0.999968
0.02 0.507978 0.846136 0.978308 0.998736 0.999971
0.04 0.515953 0.850830 0.979325 0.998817 0.999973
0.06 0.523922 0.855428 0.980301 0.998893 0.999975
0.08  概率论Exam代写 0.531881 0.859929 0.981237 0.998965 0.999977
0.10 0.539828 0.864334 0.982136 0.999032 0.999979
0.12 0.547758 0.868643 0.982997 0.999096 0.999981
0.14 0.555670 0.872857 0.983823 0.999155 0.999983
0.16 0.563559 0.876976 0.984614 0.999211 0.999984
0.18 0.571424 0.881000 0.985371 0.999264 0.999985
0.20 0.579260 0.884930 0.986097 0.999313 0.999987
0.22 0.587064 0.888768 0.986791 0.999359 0.999988
0.24 0.594835
0.892512
 0.987455 0.999402 0.999989
0.26 0.602568 0.896165 0.988089 0.999443 0.999990
0.28 0.610261 0.899727 0.988696 0.999481 0.999991
0.30 0.617911 0.903200 0.989276 0.999517 0.999991
0.32 0.625516 0.906582 0.989830 0.999550 0.999992
0.34 0.633072 0.909877 0.990358 0.999581 0.999993
0.36 0.640576 0.913085 0.990863 0.999610 0.999993
0.38 0.648027 0.916207 0.991344 0.999638 0.999994
0.40 0.655422 0.919243 0.991802 0.999663 0.999995
0.42 0.662757 0.922196 0.992240 0.999687 0.999995
0.44 0.670031 0.925066 0.992656 0.999709 0.999996
0.46 0.677242 0.927855 0.993053 0.999730 0.999996
0.48 0.684386 0.930563 0.993431 0.999749 0.999996
0.50 0.691462 0.933193 0.993790 0.999767 0.999997
0.52 0.698468 0.935745 0.994132 0.999784 0.999997
0.54 0.705401 0.938220 0.994457 0.999800 0.999997
0.56 0.712260 0.940620 0.994766 0.999815 0.999997
0.58 0.719043 0.942947 0.995060 0.999828 0.999998
0.60 0.725747 0.945201 0.995339 0.999841 0.999998
0.62 概率论Exam代写 0.732371 0.947384 0.995604 0.999853 0.999998
0.64 0.738914 0.949497 0.995855 0.999864 0.999998
0.66 0.745373 0.951543 0.996093 0.999874 0.999998
0.68 0.751748 0.953521 0.996319 0.999883 0.999999
0.70 0.758036 0.955435 0.996533 0.999892 0.999999
0.72 0.764238 0.957284 0.996736 0.999900 0.999999
0.74 0.770350 0.959070 0.996928 0.999908 0.999999
0.76 0.776373 0.960796 0.997110 0.999915 0.999999
0.78 0.782305 0.962462 0.997282 0.999922 0.999999
0.80 0.788145 0.964070 0.997445 0.999928 0.999999
0.82 0.793892 0.965620 0.997599 0.999933 0.999999
0.84 0.799546 0.967116 0.997744 0.999938 0.999999
0.86 0.805105 0.968557 0.997882 0.999943 0.999999
0.88 0.810570 0.969946 0.998012 0.999948 0.999999
0.90 0.815940 0.971283 0.998134 0.999952 1.000000
0.92 0.821214 0.972571 0.998250 0.999956 1.000000
0.94 0.826391 0.973810 0.998359 0.999959 1.000000
0.96 0.831472 0.975002 0.998462 0.999963 1.000000
0.98 0.836457 0.976148 0.998559 0.999966 1.000000
概率论Exam代写
概率论Exam代写

更多代写：数据库代写辅导  生物学网课代考  说明文Essay代写  市场营销代写Essay  实验论文代写  美国物理代考

合作平台：essay代写 论文代写 写手招聘 英国留学生代写

 

天才代写-代写联系方式