MSIN203P: MATHEMATICAL FOUNDATIONS OF MANAGEMENT III
EXAMINATION PAPER
MAY 2018
概率论考试助攻代写 This examination will last THREE (3) hours.It consists of SEVEN (7) questions. You must answer all questions.You are advised to allocate ···
This examination will last THREE (3) hours.
It consists of SEVEN (7) questions. You must answer all questions.
You are advised to allocate your time between the the di↵erent questions in proportion to the marks available.
There is no formula sheet provided.
1.[15 points] 概率论考试助攻代写
Suppose that there are 25 di↵erent types of coupons and suppose that each time one obtains a coupon, it is equally likely to be any one of the 25 types, independentlyof other Compute the expected number of di↵erent types that are contained in a set of 10 coupons.
2.[20points]
The joint pdf of X and Y is given by

3.[10points]
Let X1, X2, …, Xn be independent random variables, each having a uniform distribution over (0, 1). Let M = max{X1, X2, …, Xn}.
(a)[6points] What is the cumulative distribution function (cdf) of M ?
(b)[4points] What is the probability density function (pdf) of M ?
4.[15points] 概率论考试助攻代写
From a group of 8 women and 6 men a committee consisting of 3 men and 3 women is to be How many di↵erent committees are possible if
(a)[5points] 2 of the men refuse to serve
(b)[5points] 2 of the women refuse to serve
(c)[5 points] 1 man and 1 woman refuseto serve together.
5.[5points]
Let X be a nonnegative continuous random variable with probability density function (pdf) denoted by fX(x). Write the variance of X, var[X], in terms of fX(x).
6.[15 points] 概率论考试助攻代写
The state of a process changes daily according to a two-state Markov chain. The two states are denoted by “0” and “1” and the transition probabilities betweenthe states are given by the following:
P0,0 = 0.4, P0,1 = 0.6 P1,0 = 0.2 and P1,1 = 0.8.
Additionally, every day a message is sent. If the state of the Markov chain that day is i then the message sent is “good” with probability pi and is “bad” with probability qi = 1-pi,i = 0, 1. For example, if we are in state 0 on a given day, then the probability of sending a good message on that day is p0, and if we are in state 1 on a given day, then the probability of sending a good message on that day is p1. For the following parts, you can express your answers in terms of p0 and p1.
(a)[5 points] If the process is in state 0 on Monday, what is the probability that a goodmessage is sent on Tuesday?
(b)[5points] In the long run, what proportion of messages are good?
(c)[5 points] Define a new variable Ynsuch that Yn = 1 if a good message is sent on day n, and let it equal 2 otherwise. Is Yn,n 1 a Markov chain? If so, give its transition probability matrix. If not, then briefly discuss why not.
7.[20points] 概率论考试助攻代写
Suppose that there are two clerks that work at the post offi You arrive to the post office at a moment when both clerks are busy but there is no one else waiting in line. You will enter service as soon as either clerk becomes free, that is if the first clerk becomes free before the second, then you will go to the first clerk, and vice versa. The service times, Si, for clerk i are independent exponential with rate Li, i = 1, 2. That is, successive service times at the same server are independent, and service times across the two servers are independent. Recall that an exponential random variable X with rate L has a probability density function:
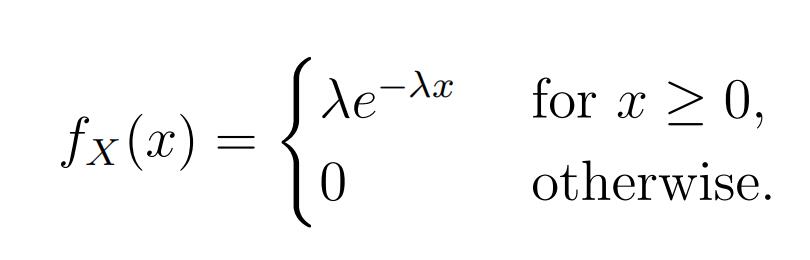
(a)[5 points]What P(S1 S2)?
(b)[5points] Find E[R], where R is the amount of time until you enter
(c)[10 points] Find E[T ], where T is the total amount of time that you spend at the postoffi

其他代写:考试助攻 program代写 cs作业代写 加拿大代写 essay代写 北美代写 北美作业代写 数据分析代写 澳大利亚代写 英国代写 homework代写 web代写 finance代写 Exercise代写
