Department of Computer Science, University College London
COMP0045 Probability Theory and Stochastic Processes
Dr Guido Germano
概率论作业代写 Choose one of the following questions for further reading and write a brief report/essay of a few (2–5) pages with single-spaced lines.
Alternative assessment 2019–2020
Choose one of the following questions for further reading and write a brief report/essay of a few (2–5) pages with single-spaced lines. Writing more will not be penalised, but sheer length does not necessarily lead to a higher mark: quality is more important.
LATEX(with the standard document class article) is recommended because it is the system of choice for typesetting mathematic and scientific texts, for which it gives the best results, but alternatively you may resort to an editor like Word, Pages, LibreOffice,etc., or to handwriting. Please upload a PDF in Part 1 and the source code (.tex, .bib,.docx, etc.) in Part 2.
The marking criteria are similar to those for the dissertation on your summer project, that are described in detail on the Moodle pages of COMP0076/77.
Questions 概率论作业代写
1. Stochastic integral
At the end of the module we have briefly discussed the stochastic integral
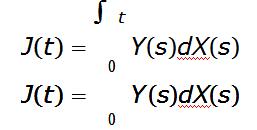
where both X(t) and Y (t) are stochastic processes, in particular for the special case where X(t) and Y (t) are continuous-time random walks, and looked at Sections II and III ofGuido Germano, Mauro Politi, Enrico Scalas, Ren´e L. Schilling, “Stochastic calculus for uncoupled continuous-time random walks”, Physical Review E 79 (6), 066102, 2009, DOI 10.1103/PhysRevE.79.066102, available on the Moodle page of COMP0045.概率论作业代写
At least, report what you have understood from there; if possible, extend to the more general case by looking up a standard book, e.g. the beginning of Chapter 4 of
Crispin W. Gardiner, Stochastic Methods — A Handbook for the Natural and Social Sciences, 4th edition, Springer, Berlin, 2009.

2. Feynman-Kac theorem 概率论作业代写
On page 104 of the lecture notes we have briefly seen the link between the Fokker-Planck equation and a stochastic differential equation. This link is given by the Feynman-Kac theorem. Look up a proof and report it. If you find more proofs with the same or different conditions, you are welcome to report them with a brief discussionand context.
3. Jaynes’ principle of maximum entropy
In the slides 54 we have briefly stated Jaynes’ principle of maximum entropy and cited the original references
E.T. Jaynes, “Information theory and statistical mechanics”, Physical Review 106 (4), 620–630, 1957, DOI10.1103/PhysRev.106.620.概率论作业代写
E.T.Jaynes, “Information theory and statistical mechanics II”, Physical Review 108 (2), 171–190, 1957, DOI 10.1103/PhysRev.108.171.
See also, from the literature section,
Edwin T. Jaynes, edited by G. Larry Bretthorst, “Probability Theory: The Logic of Sci- ence”, Cambridge University Press, Cambridge, 2003, DOI 10.1017/CBO9780511790423, PDF available through the UCL Library.概率论作业代写
and
John E. Shore, Rodney W. Johnson, “Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy”, IEEE Transactions on Informa- tion Theory 26 (1), 26–37, 1980, PDF available on https://bayes.wustl.edu/Manual/Ax iomaticDerivation.pdf.
Select one or more parts you like of these references or any others you may find and report.
4. Jaynes’ approach to differential entropy 概率论作业代写
In the slides 53 we have discussed the difficulties in properly defining differential entropy,and observed that in 1962 Edwin T. Jaynes suggested that differential entropy can be in- troduced as the limit of increasingly dense discrete distributions, obtaining an expression similar to the Kullback-Leibler divergence. See e.g. Section 4.b in
E.T.Jaynes, “Information theory and statistical mechanics”, Brandeis Lectures in Theo- retical Physics 3, 181–218, Benjamin, New York, 1963, https://bayes.wustl.edu/etj/article s/brandeis.pdf,
or any reference you may find, and report.

其他代写:代写CS C++代写 java代写 r代写 金融经济统计代写 matlab代写 web代写 app代写 作业代写 物理代写 数学代写 考试助攻
