概率论代考考试助攻数学代考

Exam 2

概率论代考 Your answer to each question (or sub-question), should be contiguous as you will have to clearly mark where your answer is when submitting

Theory of Probability Wednesday November 11, 2020 2:00pm – 3:15pm 概率论代考

Your answer to each question (or sub-question), should be contiguous as you will have to clearly mark where your answer is when submitting to Gradescope.
No collaboration allowed.
Nooutside sources allowed (no notes, no books, ).
Only scientific calculators are allowed.概率论代考
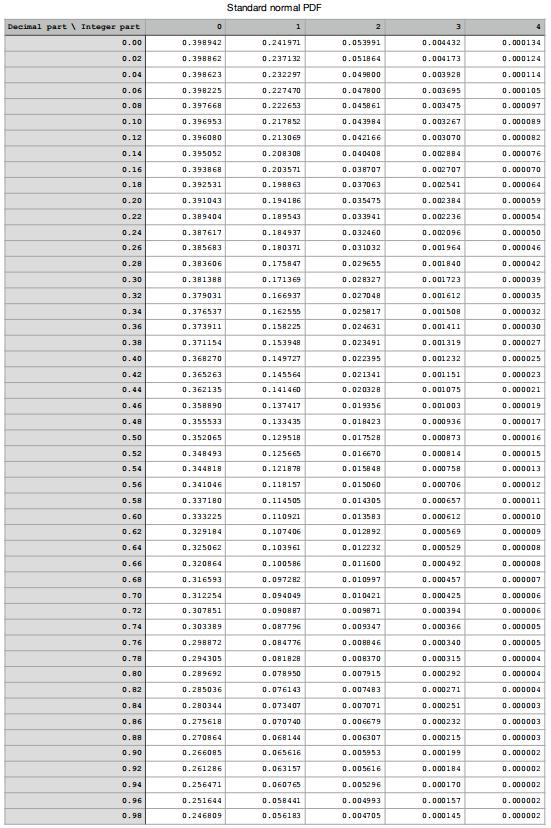
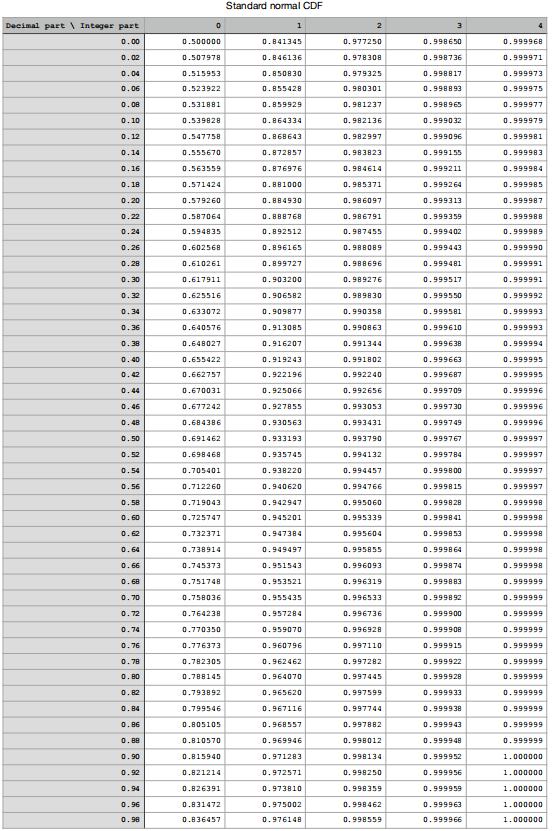
Tablesof the standard normal PDF and CDF are included.
Nocredit will be given without showing ALL work.
Pleaseplace a box around your answer for each question.
A scanned PDF must be uploaded to Gradescope by 3:25pm. No late submissions will be accepted.

Useful Random Variables 概率论代考

Binomial(n,p) distribution, k = 0, . . . , n

P[X = k] = .nΣp^k(1 − p)n−k (1)

Poisson(λ)distribution, k = 0, . . . , n

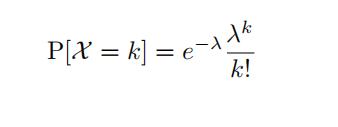
Gamma(α,λ) distribution, x > 0

Standardnormal distribution, −∞ < x < ∞

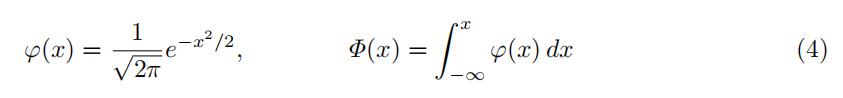
Exponential(λ)distribution, x > 0

f (x) = λ e−λx (5)

1.Nationwide, the Math SAT exam has an average score of 500 (out of 800) and a standard deviationof 120 (assuming a normal distribution).概率论代考

（a）[ 5 points ] If five students who took the exam are selected at random, what is the probabilitythat exactly two of them scored at least 680?

(b)[ 5 points ] What is the probability that a randomly chosen senior scored less than400?概率论代考

2.[ 5 points ] An insurance company insures 3000 people, each of whom will be in an accident with probability 0.001. Approximate the probability that the insurance company will have to payout on at most 2

3.[ 5 points ] The median of a random variable X is the value x such that P[X ≤ x] = 0. Compute the median of X ∼Exponential(3).概率论代考

4.[ 10 points ] The mode of a continuous random variable is the value x which maximizes f (x), where f is the probability density function of . Find the mode of a Gamma(4.5, 0.5) random

5.Considerthe discrete random variable X with probability mass function P[X = n] = C 3−|n|, for

n = . . . , −2, −1, 0, 1, 2, . . ..

(a)[ 3 points ] Find C.

(b)[ 3 points ] ComputeE[X ].

(c)[ 4 points ] What is P[X 2 = k] for k= 0, 1, 2, . . .?概率论

6.Considerthe discrete random variable X defined by its probability mass function:

P[X = 0] = 0.20, P[X = 2] = 0.10,

P[X = 1] = 0.20, P[X = 3] = 0.50.

[ 5 points ] What is the expected value, µ, of X?

[ 5 points ] What is the variance, σ², of X?(6)概率论代考

[ 10 points ] Let X ∼ Binomial(123, 0.40). Use the normal approximation to the binomial distribution to estimate P[X= 42].
[ 5 points ] Let Z be a standard normal random variable, with PDF denoted by ϕ and CDF denoted by Φ. Let X = Φ(Z). How is Xdistributed?
[ 5 points ] Let the random variable X ∼ Exponential(λ). Compute the probability density function of Y = F (X ), where F is the CDF ofX .概率论代考
Let the random variable Z ∼ N (0,1).
- [ 7 points ] Compute the probability density function of Y =Z2.
- [ 3 points] What kind of random variable is ? (Hint: Look at the PDFs on the first page of the )
Considerthe continuous random variable X with density function f (x) = Cxe⁻²^x for x ≥
- [ 3 points] What is C?
- [ 3 points ] Find the distribution function F.
- [ 4 points ] What is P[X ≥1]?
[ 10 points ] Let X ∼ Exponential(λ), and Y = log X (i.e. the natural logarithm of X ). What isthe probability density function for Y?