FINAL EXAM
MTH 361 INTRODUCTION TO PROBABILITY
概率考试代写 Problem 1 (10 points).A fair die is rolled until the first time T that a six turns up. Find the conditional probability P(T > 8 | T > 4).
Problem 1 (10 points).
A fair die is rolled until the first time T that a six turns up. Find the conditional probability P(T > 8 | T > 4).
Problem 2 (10 points). 概率考试代写
Let X be a random variable normally distributed with parameters µ = 70, σ = 10. Estimate P(X > 90).
Problem 3 (10 points). 概率考试代写
A fair coin is tossed three times. Let X be the number of heads that turn up. Find E(X) and V (X).
Problem 4 (10 points). 概率考试代写
Let X be a random variable with range [−1, 1] and let fX(x) = (3/2)x2 for |x| ≤ 1 be the density function of X. Find E(X) and V (X).
Problem 5 (10 points).
Let X1 and X2 be independent random variables with common distribution
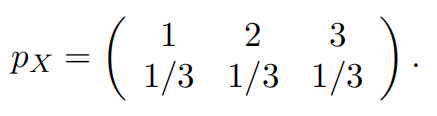
Find the distribution of the sum X1 + X2.
Problem 6 (10 points).
Suppose that X and Y are independent random variables with density functions
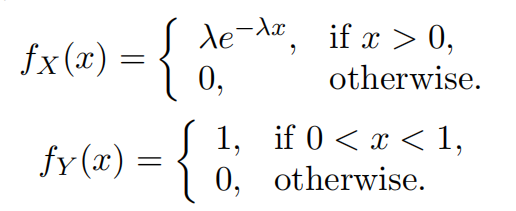
Let Z = X + Y . Find the density function fZ.

更多代写:计算机homework代写价格 多邻国代考 英国law网课作业代写代修 北美网课代写essay润色 report代写北美 留学生代写大学作业
