Course code & title : CS5487 Machine Learning
机器学习考试代做 Time allowed : Two hours Format : Online 1.The following resources are allowed on the exam: You are allowed a cheat sheet that is one A4 page
Time allowed : Two hours
Format : Online
1.The following resources are allowed on the exam:
- You are allowed a cheat sheet that is one A4 page (double-sided) handwritten with pen or pencil.
2.All other resources are not allowed, e.g., internet searches, classmates, other textbooks.
3.Answer the questions on physical paper using pen or pencil.
- Answer ALL questions.
- Remember to write your name, EID, and student number at the top of each answer paper.
4.You should stay on Zoom during the entire exam time.
- If you have any questions, use the private chat function in Zoom to message Antoni.
5.Final submission
- Take pictures of your answer paper and submit it to the “Final Exam” Canvas assignment. You may submit it as jpg/png/pdf.
- It is the student’s responsibility to make sure that the captured images are legible. Illegible images will be graded as is, similar to illegible handwriting.
Statement of Academic Honesty 机器学习考试代做
Below is a Statement of Academic Honesty. Please read it.
I pledge that the answers in this exam are my own and that I will not seek or obtain an unfair advantage in producing these answers. Specifically,
- I will not plagiarize (copy without citation) from any source;
- I will not communicate or attempt to communicate with any other person during the exam; neither will I give or attempt to give assistance to another student taking the exam; and
- I will use only approved devices (e.g., calculators) and/or approved device models.
- I understand that any act of academic dishonesty can lead to disciplinary action.
I pledge to follow the Rules on Academic Honesty and understand that violations may led to severe penalties.
Name:
EID:
Student ID:
Signature:
(a) If you have not already, copy the entire above statement of academic honesty to your answer sheet. Fill in your name, EID, and student ID, and sign your signature to show that you agree with the statement and will follow its terms.
Problem 1 EM for MAP estimation [25 marks] 机器学习考试代做
Let X be the observed data, Z the corresponding hidden values, and θ the parameters. We will use the EM algorithm to find the MAP solution of θ, i.e., the maximum of the posterior distribution over parameters p(θ|X). In the E-step, we obtain the MAP Q function by taking the expectation of the posterior log p(θ|X, Z),

Problem 2 BDR with unbalanced loss function [25 marks]
Consider a two-class problem with y ∈ {0, 1} and measurement x, with associated prior distribution p(y) and class-conditional densities p(x|y). In this problem, assume that the loss-function is:
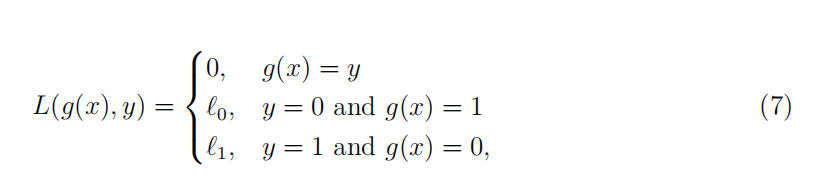
where g(x) is the classifier prediction for x. In other words, the loss for misclassification is different for each class.
(a) [5 marks] When might this type of loss function be useful? Can you give a real-world example?
(b) [5 marks] Derive the Bayes decision rule (BDR) for y. Write the BDR as a log-likelihood ratio test. What is the threshold?

Problem 3 Soft-margin SVM with 2-norm penalty [25 marks] 机器学习考试代做

ξi is the slack variable that allows the ith point to violate the margin, and C the hyperparameter.
(a) [5 marks] Show that the non-negative constraint ξi ≥ 0 is redundant, and hence can be dropped.
(b) [5 marks] Let αi be the Lagrange multiplier for the i-th inequality constraint. Write down the Lagrangian L(w, b, ξ, α) for the problem. Derive conditions for the minimum of L(w, b, ξ, α) w.r.t. {w, b, ξ}.
(c) [10 marks] Derive the dual function L(α) = minw,b,ξ L(w, b, ξ, α), and write down the dual problem for SVM with 2-norm.
(d) [5 marks] Comment on the similarity and differences between the dual problems for the SVM with 2-norm penalty and the original SVM with 1-norm penalty. What is the interpretation of any differences?
Problem 4 Kernel perceptron [25 marks] 机器学习考试代做
For a training set D = {(x1, y1), . . . ,(xn, yn)}, where xi ∈ Rd and yi ∈ {+1, −1}, the Perceptron algorithm is as follows:
Perceptron algorithm
1: set w = 0, b = 0, R = maxi ||xi || 2: repeat 3: for i = 1, . . . , n do 4: if yi(wTxi + b) ≤ 0 then 5: set w ← w + ηyixi 6: set b ← b + ηyiR2 7: end if 8: end for 9: until there are no classification errors
For an x∗ input, the classifier is y∗ = sign(wTx∗ + b).

(c) [5 marks] What is the interpretation to the parameters αi?
(d) [5 marks] Using (b) derive an equivalent Perceptron algorithm (the dual perceptron).
(e) [5 marks] Apply the kernel trick the dual perceptron algorithm to obtain the kernel perceptron algorithm. What is the kernelized decision function?

