UNIVERSITY COLLEGE LONDON
machine learning algorithm代写 •Assignment Release Date: 2nd October 2019•Assignment Hand-in Date: 16th October 2019 at 11.55am•Format: Problems
Faculty of Engineering Sciences
Department of Computer Science
COMP0036: LSA – Assignment 1
Dr. Dariush Hosseini ([email protected])
Overview machine learning algorithm代写
- Assignment Release Date: 2nd October2019
• Assignment Hand-in Date: 16th October 2019 at 11.55am
- Format:Problems
Guidelines machine learning algorithm代写
- You should answer all THREE questions.
- Note that not all questions carry equal marks.
- You should submit your final report as a pdf using Turnitin accessed via themodule’s Moodle page.
- Within your report you should begin each question on a newpage.
- You should preface your report with a single page containing, on two lines:–The module code:‘COMP0036’
–The assignment title: ‘LSA – Assignment1’
- Your report should be neat andlegible.
You are strongly advised to use LATEX to format the report, however this is not a hard requirement, and you may submit a report formatted with the aid of another system, or even a handwritten report, provided that you have converted it to a pdf (see above).machine learning algorithm代写
- Pleaseattempt to express your answers as succinctly as possible.
- Please note that if your answer to a question or sub-question is illegible orincomprehen- sible to the marker then you will receive no marks for that question or sub-question.
- Please remember to detail your working, and state clearly any assumptions which you make.
- Unless a question specifies otherwise, then please make use of the Notation section as a guide to the definition of objects.machine learning algorithm代写
- Failure to adhere to any of the guidelines may result in question-specific deduction of marks. If warranted these deductions may be punitive.
Notation
Inputs:
x = [1, x1, x2, …, xm]T ∈ Rm+1
Outputs:
y ∈ R for regression problems machine learning algorithm代写
y ∈ {0, 1} for binary classification problems
Training Data:
S = {x(i), y(i)}n
Input Training Data:
The design matrix, X, is defined as:
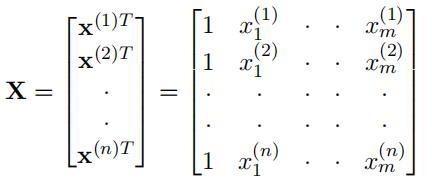
Output Training Data:
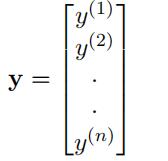
Data-Generating Distribution:
S is drawn i.i.d. from a data-generating distribution, D
1.You are given a raw training data set consisting of 50 input/output sample pairs.
Each output data point is real-valued, while each input data point consists of a vector of real- valuedattributes, x = [1, x1, x2, x3, x4, x5]T .machine learning algorithm代写
You are asked to investigate the relationship between inputs and outputs.Your domain expertise leads you to believe that the class of cubic functions will be most appropriate for the modelling of this relationship.
(a) [7 marks]
What is the problem with using the ordinary least squares approach to find such a model? Explain.
[Hint: Consider the Multinomial Theorem]machine learning algorithm代写(b) [3 marks]
If you discarded one of the attributes in your model would this problem remain? Explain.
(c) [5 marks]
Briefly describe an approach that can help to remedy the problem in part (a). Explain.
(d) [5 marks]
You are asked to select only those features which are most important for use in your model. Explain how you would achieve this in an efficient fashion.machine learning algorithm代写
2.Recall that in linear regression in general we seek to learn a linear mapping, fw,
charac- terisedby a weight vector, w ∈ Rm+1, and drawn from a function class, F:
F = {fw(x) = w · x|w = [w0, w1, …, wm] ∈ R }
Now, consider a data-generating distribution described by a Gaussian additive noise model:
y = w · x + s where: s ∼ N (0, α), α > 0
Assume that x is one dimensional, and that there is no bias term to learn, i.e. x = x ∈ R and w = w ∈ R.machine learning algorithm代写
(a) [4 marks]
Given a training set, S, find an expression for the likelihood, pD(S|w) = P[S|w] in the form: A exp (B). Characterise A and B.
(b) [4 marks]
Assume a prior distribution, pW (w), over w, such that each instance of w is an outcome of a Gaussian random variable, W , where:
W ∼ N (0, β) where: β > 0
Provide a detailed characterisation of the posterior distribution over w.
(c) [4 marks]
Hence succintly derive the Maximum A Posteriori (MAP) estimate of w.
(d) [4 marks]machine learning algorithm代写
Is this solution unique? Explain.
(e) [4 marks]
This approach should remind you of another machine learning algorithm. State the algorithm, and express the connection between the two.
3.(a) [2marks]
Describe the discriminative approach to classification. How does it differ from the generative approach?
(b) [3 marks] machine learning algorithm代写
Recall that in binary logistic regression, we seek to learn a mapping characterised by
the weight vector, w and drawn from the function class, F:
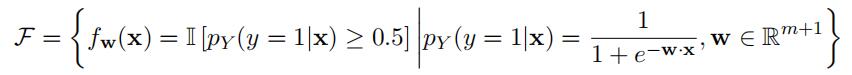
Here pY (y|x) is the posterior output class probability associated with a data generating distribution, D, which is characterised by pX,Y (x, y).
Provide a motivation for this form of the posterior output class probability pY (y|x) byconsidering a Logistic Noise Latent Variable Model. Remember that the noise in sucha model characterises randomness over the outcomes, ε, of a random variable, s, which is drawn i.i.d. as follows:
s ∼ Logistic(a, b) where: a = 0, b = 1
The characteristic probability distribution function for such a variable is:
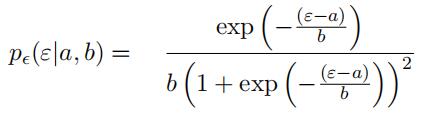
(c) [3 marks]
If we allow the Logistic parameters to take general values a ∈ R, b > 0 explain the effect which this has on the final logistic regression model.
(d) [4 marks]
Let us assume instead a Gaussian Noise Latent Variable Model. Now s is drawn i.i.d. as follows:
s ∼ N (0, 1)
Derive an expression for the posterior output class probability pY (y|x) in this case.
(e) [3 marks]machine learning algorithm代写
How will the treatment of outliers in the data differ for these two models? Explain.
(f) [2 marks]
For K-class multinomial regression, assuming misclassification loss, we can express a discriminative model for the posterior output class probability as:
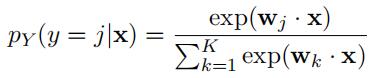
Demonstrate that this model reduces to logistic regression when K = 2.
(g) [3 marks]machine learning algorithm代写
For K > 2 derive an expression for the discriminant boundaries between classes. What does this expression describe?

其他代写:考试助攻 计算机代写 java代写 function代写 paper代写 web代写 编程代写 report代写 数学代写 algorithm代写 金融经济统计代写 finance代写 python代写 java代写 code代写 project代写 Exercise代写 dataset代写 analysis代写
