Optimize the Portfolio of Soybean Varieties at Target Farm through Machine Learning
机器学习报告代写 The important result of this project is the portfolio of 5 soybean varieties and the specific land allocation for the target farm.
Abstract
The world is facing the problem of food shortages due to the following three reasons. Firstly, the population of the world has grown rapidly. Secondly, urbanization has led to a decrease in the area of food planting. Thirdly, the COVID-19 is seriously affecting production globally. Therefore, it is imperative to select the best soybean varieties to increase yields and thus the food shortage may be alleviated.
This project will use machine learning to optimize the soybean variety portfolio of the target farm by selecting 5 kinds of soybeans from 182 varieties and allocating a certain amount of land for them to optimize production. Descriptive analytics, predictive analytics and prescriptive analytics will all be used in this project.
Descriptive analytics mainly studies the influence of location on the yield, the relationship between the weather and location, the distribution of yields and varieties as well as if there are enough data to build a model.
The specific methods of predictive analytics are Linear Regression, LASSO, Regression Tree, Bagging, Random Forest, Boosted Trees and Neural Network. These methods will be used to build models, predict yield and compare accuracy. Finally, in prescriptive analytics, the mean risk heuristic is applied to give the final result of questions. Both predicted average yield given by the models and mean square error indicated the risk of growing the varieties will be considered in this part. 机器学习报告代写
The ultimate goal of the project is to provide the optimal soybean varieties through machine learning to achieve the goal of increasing yield per unit area. The final result will help soybean farmers increase their yields and reduce the stress of starvation for people in certain area. Therefore, it is of great significance to conduct this research.
Keywords: Food Shortage, Optimization, Portfolio of Soybean Varieties, Machine Learning
Introduction 机器学习报告代写
Food shortages have now become a global problem. This is because, on the one hand, the world’s population has grown tremendously. In the past 200 years, the world’s population has increased by 750%, from 1 billion to about 7.5 billion. On the other hand, urbanization has led to a decrease in rural areas and cultivated land, thus food shortages have become more serious. In addition, a special influencing factor emerged that the impact of the COVID-19 is gradually deepening.
The World Food Program pointed out that 135 million people around the world were facing severe food shortages before, and now affected by the epidemic, this data is expected to increase by about 130 million people this year to 265 million people. In this case, it is particularly important to increase grain production per unit area. This has become the motivation of this project to increase the yield and solve difficult food shortage problem by selecting the best soybean varieties.
The goal of this project is to optimize the portfolio of soybean varieties at target farm through machine learning.
The specific question of this project is to that 5 varieties of soybeans is selected from 182 kinds of soybeans for the target farm and a certain land is allocated as the portfolio so that the yield could be optimized. If the results are convincing and credible, there will be benefits for many people in the world, such as farmers who grow soybeans, people who are starving, especially children who are malnourished due to food shortages. Therefore, it is significant to do this research. 机器学习报告代写
The analysis includes three components: descriptive analytics, predictive analytics, and prescriptive analytics. To be more specific, descriptive analytics mainly studies some qualitative and descriptive questions to understand the general situation of the data related to the question. In predictive analytics, 7 methods are used to build models for different varieties and predict the yield for the target farm. All methods are compared accuracy by the mean square error. Finally, in the prescriptive analytics part, the Mean-Risk Heuristics that considered both average yield and risk is applied to give the final portfolio of the question.
The important result of this project is the portfolio of 5 soybean varieties and the specific land allocation for the target farm. This indicates that through machine learning, the optimal varieties can be selected, and the purpose of increasing the yield per unit area could be achieved. Such experience may also be applied in other target areas, which may help solve the problem of food shortages on a larger scale.
Literature Review
Some articles have studied the problem of increasing soybean or other grain yields by optimizing variety selection. For example, Huang et al. (2020) performed inter-comparison method in “Comparative Test Analysis and Evaluation of New Summer Soybean Varieties (lines) in Xinxiang Area”. “Effects of planting patterns on agronomic characters and yield of different soybean varieties” (Wang et al., 2020) applied algorithms for the purpose of constructing a reasonable group structure of soybeans and increasing yields. The structure and methods of these studies are of reference significance.
“Machine-Learning-Based Simulation for Estimating Parameters in Portfolio Optimization:
Empirical Application to Soybean Variety Selection” (Sundaramoorthi & Dong, 2019) is more instructive because the method is totally Machine-Learning-Based. Bagging, Random Forest and Regression Trees methods were used which can provide a theoretical basis for this project. Barkley, Peterson & Shroyer (2010) conduct a study using portfolio theory in business investment analysis to find the best portfolio of wheat varieties with maximum yield and minimum risk. This article inspired me to consider both risk and yield comprehensively. 机器学习报告代写
However, these studies (Basnet, Mader & Nickell, 1974; Cui et al., 2020) usually only use 1 to 2 methods for modeling and prediction. In fact, each method has drawbacks and shortcomings. Adding more methods can make the results better and more unbiased. Also, it is more likely to apply the method to other regions to increase the scope of problem solving. This project will try to fill this research gap.

Methodology and Analysis
There are three components of the methodology: descriptive analytics, predictive analytics, and prescriptive analytics. Before this three steps, data pre-processing is also an important step because it will provide a solid foundation for subsequent analysis.
Step 1: Data Pre-processing
In this step, the data is divided into two types: sufficient and insufficient. Sufficient data is directly retained, and insufficient data is merged. Taking less than 50 data as the criterion for inadequate data, among all 182 varieties, 99 are insufficient and 83 are sufficient. Synthesize 99 insufficient data into a new variety, called “Vnew”, and participate in the fitting together with the other 83, a total of 84 varieties. In the subsequent fitting, each method will build 84 models. There are also other operations for subsequent fitting. 机器学习报告代写
Step 2: Descriptive Analytics
This part is mainly to have a general understanding of the data. Firstly, plot the latitudes and longitudes on a map to visualize the locations of farms in Figure 1.
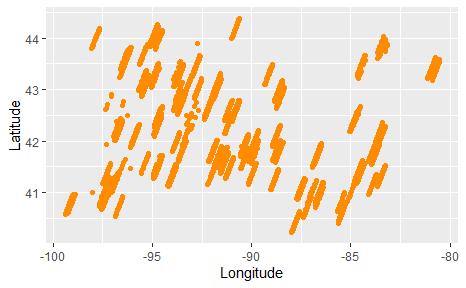
Figure 1. Location Information of the farms in the given data.
Secondly, generate frequency distribution for varieties in Figure 2.
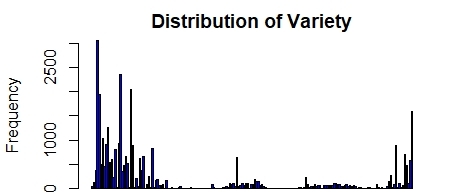
Figure 2. The Frequency of the Variety for all data.
It is apparent from Figure 2 that the amount of data of different types varies greatly, and there are situations where the amount of data is sufficient and insufficient. We have already processed this part in Step 1, which will benefit the quality of subsequent models.
Thirdly, check to see if there is any relationship between the locations and varieties. Linear regression method is selected here, by observing the p-value and coefficient to judge the relationship between the locations and yield of varieties. Both longitude and latitude have a significant impact on yield because they have p-values close to 0. The coefficient of longitude is -0.33 which is hard to judge whether its impact on production is positive or negative. The coefficient of latitude is -2.74, which obviously shows that the lower the latitude, the greater the yield.
Fourthly, explore relationships between locations and weather related variables.
Through the linear regression, it can be proved that both factor Weather 1 and 2 positively influence the locations. This is because the two p-values are close to 0 and the coefficient of Weather 1 and 2 are 1.09 and 1.97 respectively. 机器学习报告代写
Fifthly, plot the distribution of the yield variable in Figure 3. Figure 3 describes a normal distribution of the variety yield and indicates that the yield between different varieties varies greatly. Therefore, the goal of this project should be select the better varieties to improve the total yield.
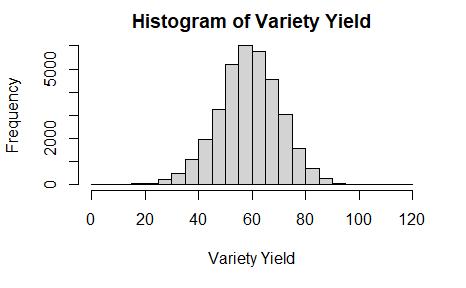
Figure 3, the histogram of the Variety yield.
Step 3: Predictive Analytics
The target variable is Variety_Yield in this project. The 84 varieties including 83 varieties with sufficient data and 1 new variety call “Vnew” consisting of all varieties with insufficient data will be used to build the model. 7 methods including Linear Regression, LASSO, Regression Tree, Bagging, Random Forest, Boosted Trees and Neural Network are applied here. 机器学习报告代写
The steps to build a model for each method are similar. Firstly, divide all data into training set and test set and ratio is 8:2. Secondly, predict the yield of all 84 varieties by the “for” loop code. More specifically, fit the training data and predict the test set. Calculate the mean square error (MSE) to test the accuracy of the method. Finally, perform the prediction of the yield of the evaluation data for the target farm.
There are several points to note among the seven methods. Firstly, LASSO is different from other methods.
It requires performing regression processing on the data frame before fitting. Secondly, even though the data was pre-processed in advance, an error occurred in the loop of the Boosted Trees method. The reason was that the data was insufficient. This problem was properly solved by adjusting the loop range. Thirdly, the Neural Network method needs to standardize the data before fitting. The formula for standardization is (X-min)/(max-min).
The result of the prediction could be seen below in Table 1.
Table 1. Predicted yield of different varieties through different method.
| Variety | Linear Regression | LASSO | Regression Tree | Bagging | Random Forest | Boosted Trees | Neural Network |
| V100 | 112.6819803 | 65.18063591 | 70.02227682 | 64.68006616 | 64.75130555 | 65.56819895 | 86.55001021 |
| V101 | 100.1761093 | 57.02092699 | 58.74248239 | 57.74756935 | 58.30591639 | 55.62336377 | 88.47904301 |
| V102 | 57.76424079 | 63.62861206 | 57.69892858 | 61.57844969 | 61.99542259 | 67.6825447 | 99.95074506 |
| V103 | 61.50147159 | 66.18768647 | 43.16572425 | 58.52990743 | 59.01815772 | 52.74332988 | 97.4743919 |
| V104 | 90.04583615 | 63.24537448 | 59.34155904 | 59.26660596 | 58.32978547 | 63.62265776 | 93.09393859 |
| V105 | 63.28664144 | 64.15628013 | 55.70881625 | 58.05946715 | 58.90818474 | 60.43203184 | 115.6697742 |
| V106 | 95.18119428 | 60.95025391 | 58.4372731 | 59.56121281 | 59.88475096 | 50.18138299 | 85.86605985 |
| V107 | 64.58351253 | 68.63657536 | 60.47064032 | 58.61390831 | 58.06799915 | 60.6825476 | 99.61836252 |
| V108 | 74.59180266 | 62.52148554 | 48.33331444 | 55.39438697 | 55.03133129 | 58.54584829 | 92.79804262 |
| V109 | 62.2590398 | 64.41932599 | 55.19891827 | 56.13975415 | 58.01575387 | 64.61644134 | 91.75252446 |
| V110 | 70.73957641 | 61.19700908 | 60.79995268 | 60.93484401 | 60.3007325 | 62.71432929 | 87.6647739 |
| V111 | 63.12875576 | 67.55673962 | 59.19266437 | 58.04586013 | 56.63538705 | 52.10891863 | 86.72573571 |
V112 |
73.0723474 | 66.90948133 | 56.22177384 | 58.72016627 | 59.03399816 | 64.61683611 | 89.72766442 |
| V114 | 59.51929313 | 60.99421047 | 54.84387274 | 57.10822593 | 57.8543227 | 54.00845871 | 85.30094106 |
| V115 | 62.25947432 | 64.37366175 | 69.82979417 | 58.83971293 | 57.86527428 | 50.02048224 | 102.5309678 |
| V116 | -929.4503032 | 47.83455902 | 54.15194142 | 49.7853575 | 49.39766396 | 50.32464398 | 73.12323454 |
| V117 | 62.45410717 | 58.99087959 | 54.93492436 | 54.99392153 | 54.72097492 | 54.5991056 | 90.73609857 |
| V118 | 55.96325129 | 55.68537017 | 52.47233522 | 54.51578862 | 55.89744269 | 51.85565025 | 86.10926931 |
| V119 | 44.02900824 | 56.90416414 | 44.29714131 | 52.70952276 | 53.62105414 | 56.18499717 | 93.02048592 |
| V121 | 58.78954239 | 59.39031401 | 54.1570868 | 55.49908152 | 55.01089998 | 32.08863654 | 105.7599135 |
| V122 | 45.69461977 | 57.7078316 | 56.81222375 | 51.82878334 | 51.52560117 | 50.36948139 | 87.97906017 |
| V124 | 88.4745568 | 56.67059064 | 60.80477336 | 53.55030403 | 54.9217717 | 54.78632791 | 79.75623728 |
| V125 | -355.8928473 | 48.18237053 | 50.49200568 | 52.88173615 | 52.20755789 | 0 | 64.52248074 |
| V126 | 64.27944551 | 57.00401805 | 64.72036744 | 54.05213706 | 54.3566554 | 66.27144938 | 92.03500761 |
| V127 | 51.97222519 | 69.02170065 | 37.12745528 | 46.25098813 | 48.08354609 | 40.09954802 | 73.18214852 |
| V128 | -110.111735 | 81.46268537 | 79.81791803 | 56.25024086 | 54.9895276 | 58.31450786 | 92.01592498 |
| V130 | -295991.064 | 52.87317115 | 51.79883041 | 50.8390562 | 50.53069405 | 46.20298869 | 77.51456631 |
| V131 | 3228.775683 | 68.83773718 | 53.47943307 | 51.0921526 | 51.60233134 | 53.59107986 | 71.14493931 |
| V133 | 882237.7943 | 58.50506726 | 60.00990364 | 48.62824027 | 48.49385244 | 51.5754167 | 87.03977229 |
| V135 | -42981.98149 | 55.92438675 | 60.40135846 | 48.10611492 | 47.9690189 | 45.93819059 | 75.3090758 |
| V136 | 142776.7128 | 44.97741592 | 42.09221778 | 43.07008466 | 42.89561098 | 46.85419215 | 82.92352273 |
| V137 | -77301.8127 | 42.88827691 | 42.52617216 | 36.6968592 | 37.25211529 | 34.21647654 | 71.84029338 |
| V138 | 3312.620365 | 43.99827692 | 52.3892111 | 42.6436661 | 42.38232617 | 36.98697034 | 75.25713636 |
| V139 | -43649.94441 | 41.98683887 | 29.90236296 | 35.55724395 | 36.22138564 | 48.67731866 | 67.0473347 |
| V140 | -12285.02071 | 41.7296011 | 34.67279417 | 39.84071598 | 38.35600717 | 39.50572437 | 64.98804297 |
| V169 | -37970.0721 | 28.4695012 | 50.71726808 | 51.09414105 | 51.73651807 | 51.10642065 | 88.45234246 |
| V179 | 868.3821495 | 75.66002337 | 54.12209191 | 60.48061254 | 61.17765996 | 58.89906281 | 86.861495 |
V180 |
300.0392466 | 60.31813473 | 75.14458347 | 66.98092237 | 65.70026091 | 72.86432688 | 89.25291391 |
| V181 | -3535.110402 | 63.01954876 | 62.9838544 | 61.49756756 | 62.52623435 | 60.91804453 | 83.65247886 |
| V183 | 69.50047722 | 61.90443939 | 61.6125274 | 58.26592123 | 58.58700213 | 58.64384123 | 87.74383484 |
| V185 | 12818.14947 | 60.35110302 | 52.22385801 | 54.39711645 | 55.58875598 | 54.28898398 | 79.89387435 |
| V186 | 80.75199106 | 60.10133466 | 48.6927661 | 56.68903753 | 57.33623531 | 62.09918411 | 83.71241357 |
| V187 | 355.5063985 | 62.20440013 | 60.90305002 | 59.28488672 | 61.09158135 | 66.90738493 | 87.77214958 |
| V188 | 61.43990407 | 61.22242724 | 54.40304051 | 58.49960435 | 58.59701108 | 55.03299809 | 84.61083927 |
| V189 | 63.81374744 | 61.52924509 | 62.88808061 | 60.40639675 | 59.78986754 | 60.4744975 | 88.29118463 |
| V190 | 32.54284615 | 58.46607469 | 59.79578661 | 55.03738111 | 56.64329632 | 56.36857103 | 79.69779757 |
| V191 | 34.96283151 | 57.28432055 | 67.1188618 | 51.39759108 | 52.34676607 | 62.53797276 | 84.48099701 |
| V192 | 57.84897296 | 76.30603216 | 46.42201911 | 56.56424204 | 57.12966566 | 59.99185514 | 79.93395304 |
| V193 | 36.68941554 | 58.06421889 | 39.44389071 | 53.17233488 | 53.35921346 | 50.68375301 | 78.14500234 |
| V194 | 12570409.87 | 64.43078004 | 58.08755544 | 50.41946118 | 51.31744878 | 52.57776077 | 86.78233998 |
| V195 | 88372.32648 | 68.26771043 | 67.65027253 | 57.63376716 | 56.68007943 | 58.29651232 | 78.55092628 |
| V196 | -21581730.25 | 59.07413665 | 55.48377119 | 53.1975548 | 53.66858256 | 54.74732697 | 82.19622987 |
| V31 | -18231465.38 | 79.75719408 | 60.90651095 | 62.84662761 | 63.56252955 | 57.81897931 | 90.47262509 |
| V32 | -82364.01534 | 78.49617284 | 68.75748331 | 64.82894187 | 64.98542435 | 60.62933599 | 84.5450634 |
| V36 | 94586956.39 | 79.22139038 | 58.25863914 | 65.28044486 | 65.43308843 | 73.90618251 | 88.15588295 |
V38 |
35362.24119 | 64.64885372 | 51.23172521 | 63.543584 | 63.24707043 | 67.57525266 | 89.5136613 |
| V39 | 144837.5432 | 64.75317968 | 60.88123661 | 61.9221465 | 62.43259266 | 69.08356302 | 81.93952727 |
| V40 | 4719.304605 | 62.91058379 | 52.32644162 | 57.73106802 | 58.12714477 | 58.3782358 | 79.07237815 |
| V41 | -113811231 | 65.15025395 | 59.90649521 | 62.05799451 | 63.04924149 | 64.61736251 | 85.33566101 |
| V42 | 8085.800581 | 61.04544475 | 56.77610532 | 57.9887994 | 57.94797297 | 51.73323917 | 87.03576504 |
| V43 | 53.93564332 | 62.57085027 | 51.90648824 | 56.8506727 | 58.01553756 | 57.14109669 | 87.04316807 |
| V44 | 168.0675351 | 60.88200889 | 52.35164255 | 56.51456099 | 57.26948553 | 59.19570743 | 86.18108629 |
| V45 | 111961.7153 | 61.2391268 | 63.85091657 | 54.18753218 | 54.08018128 | 52.94394781 | 82.70367346 |
| V46 | 64.71912114 | 63.59648409 | 66.36835637 | 59.51095116 | 57.94943526 | 67.63817308 | 88.59488646 |
| V47 | 64.43590373 | 61.25594532 | 54.8607355 | 60.87768045 | 59.98495753 | 68.19862266 | 78.62697814 |
| V48 | 38.81158613 | 59.74674225 | 51.23598056 | 54.88151054 | 55.47105266 | 54.74459132 | 81.37433194 |
| V49 | -10452.05125 | 61.59371522 | 52.24030824 | 56.93075548 | 58.20986234 | 57.32381628 | 79.72989069 |
| V51 | 149042.2013 | 59.84185677 | 51.31206448 | 55.63793612 | 56.31026847 | 64.3737881 | 81.41539401 |
| V52 | -10227.39447 | 57.69102436 | 69.31505539 | 56.20734508 | 56.49324219 | 56.64307495 | 76.48343358 |
| V54 | 4374.377771 | 61.89406967 | 49.53123535 | 54.99915998 | 55.93281599 | 51.77181006 | 82.74961592 |
| V56 | 88300.6969 | 63.16869238 | 55.49762304 | 53.12815731 | 50.80869952 | 63.06396717 | 79.27525701 |
| V8 | 2425185.521 | 59.07306522 | 66.05912473 | 60.53120773 | 60.42068334 | 65.58507743 | 88.87808504 |
| V87 | -33535.75165 | 56.53485808 | 43.76346273 | 48.28065608 | 51.3300429 | 51.87624032 | 77.624912 |
| V88 | -184164.2453 | 50.76524107 | 57.26742813 | 59.2546737 | 59.24639782 | 61.05039632 | 81.82995349 |
| V9 | -305944.2698 | 74.34657329 | 58.49765809 | 58.35948305 | 58.8901849 | 73.29179773 | 83.84272849 |
| V90 | -527800957.7 | 99.02743208 | 72.24215477 | 59.63938064 | 60.4631578 | 59.32364058 | 104.8754767 |
| V92 | -766494.0612 | 45.9537126 | 43.00975128 | 56.72061643 | 58.71636854 | 64.77833997 | 84.16517855 |
V94 |
-80778.6646 | 52.12197375 | 51.92567675 | 57.7075577 | 57.76309266 | 59.69825646 | 77.53049732 |
| V95 | 3036035.183 | 37.57766531 | 51.3037449 | 60.16463488 | 61.4358126 | 54.67157376 | 90.09971169 |
| V96 | 2573032.856 | 64.94371687 | 56.4966121 | 59.01382432 | 61.70679277 | 64.07693631 | 94.53271472 |
| V97 | 27205.55249 | 60.80261568 | 67.59211554 | 61.26005455 | 61.30674414 | 55.0005536 | 89.16797002 |
| V98 | 68.86288426 | 71.82933768 | 68.89192141 | 67.1311739 | 65.29808979 | 64.24985717 | 92.38771294 |
| V99 | 84.70390657 | 72.91427377 | 58.10841352 | 61.56336709 | 60.39798121 | 65.56884353 | 101.7332391 |
| Vnew | 71.73584042 | 60.89675222 | 54.14046816 | 58.45951856 | 58.02478818 | 62.60185974 | 93.70239313 |
Step 3: Predictive Analytics
In this step, firstly the accuracy of different method should be summarized. Table 2 shows the MSE of 7 methods.
Table 2. MSE of 7 methods.

Then, assign different weights to different methods according to MSE. Since the MSE of the linear regression is too large and has no reference value, the weight is 0. Others are assigned weights 6, 5, 4, 3, 2 and 1, according to the ordering MSE from small to large. Refer Table 3 for the weights.
Table 3. Weights of 7 methods.
![]()
Next, calculate the weighted average of the yield predicted by different methods according to the weights above.
Also, the Mean-Risk Heuristics that considered both average yield and risk is applied here. Standard deviation is a good way to express risk.
By calculating the standard deviation (SD) of the yield of all the data for each variety, the uncertainty of planting this soybean is determined, which is the risk.
To combine the weighted average yield and risk, a formula balance=(average yield)^2/risk is used here because we hope to have greater yield and less risk, and the yield should be considered more than SD. After obtaining the new factor balance, order it and choose the top 5 for the final selection. According to the balance, the land is allocated proportionally. Therefore, the five selected varieties are V98, V39, V9, V90 and V31. The land allocation proportions are 20.95%, 20.59%, 20.07%, 19.47% and 18.92%, respectively. Table 4 describes the ordered balance and the corresponding weighted average yield and risk. The final allocation proportions are also shown. 机器学习报告代写
Table 4. Process and the final result of the land allocation.
| Variety | Average_yield | Risk(SD) | Balance | Allocation |
| V98 | 68.65 | 9.75 | 483.12 | 20.95% |
| V39 | 64.22 | 8.68 | 474.96 | 20.59% |
| V9 | 64.23 | 8.91 | 463.00 | 20.07% |
| V90 | 71.84 | 11.50 | 448.97 | 19.47% |
| V31 | 66.54 | 10.14 | 436.43 | 18.92% |
Conclusion 机器学习报告代写
This project uses 7 methods of machine learning including Linear Regression, LASSO, Regression Tree, Bagging, Random Forest, Boosted Trees and Neural Network to build models to analyze and predict the yield of different varieties of soybeans. Considering the accuracy of different methods, the predicted value is weighted and averaged. Risk and yield are innovatively both considered to determine the final optimal portfolio.
The final result of this project is that the five selected varieties are V98, V39, V9, V90 and V31.
The land allocation proportions are 20.95%, 20.59%, 20.07%, 19.47% and 18.92%, respectively. Also, among the 7 methods, the Bagging, Random Forest and LASSO perform the best, and linear regression and neural networks are the least suitable for this case.
Using enough methods and assigning different weights to different methods based on accuracy is the first innovation of this project, because this can make up for the shortcomings of a certain method and obtain more unbiased results. The second innovation is to summarize whether different methods are suitable for this type of data. Such experience can also be used in other regions, which can provide help for future research on soybeans or other grain varieties in more regions, so as to solve the wider food shortage problem. The finding of this project can be helpful for both soybean growers and starving people, and could be even instructive for relevant government departments to issue guiding policies on varieties.
References 机器学习报告代写
- Huang Jinhua, Wang Lingyan, Tang Zhenhai, Dou Shishu, Li Mingwei, Ma Haitao, Zhang Suping, Li Junli, Zheng Qiudao, Fan Yongsheng. Analysis and evaluation of comparative experiment of new summer soybean varieties (lines) in Xinxiang area[J]. Anhui Agricultural Sciences, 2020, 48(17):21-23+27.
- Wang He,Sun Jiaxing,Mo Yan,Yang Shuang. Effects of Planting Patterns on Agronomic Characters and Yield of Different Soybean Varieties[J].China Seed Industry,2020(12):60-63.
- Sundaramoorthi D, & Dong L. Machine-Learning-Based Simulation for Estimating Parameters in Portfolio Optimization: Empirical Application to Soybean Variety Selection[J]. SSRN Electronic Journal, 2019. 机器学习报告代写
- Barkley, A., Peterson, H., & Shroyer, J. (2010). Wheat Variety Selection to Maximize Returns and Minimize Risk: An Application of Portfolio Theory. Journal of Agricultural and Applied Economics, 42(1), 39-55.
- Basnet B., Mader E. L. & Nickell C. D., Influence of Altitude on Seed Yield and Other Characters of Soybeans Differing in Maturity in Sikkim (Himalayan Kingdom), Agronomy Journal, 1974.
- Cui Jihan, Li Shunguo, Liu Meng, Guo Shuai, Zhao Yu, Ma Junting, Xia Xueyan. The effect of millet and peanut/soybean intercropping on yield and the differences between varieties[J]. Journal of Anhui Agricultural Sciences, 2020, 48(17) :35-40+45.

