Machine Learning
机器学习作业代做 We will be using some code extracts that were implemented on the week 4 Classification I lab and build a Neural Network.
0. Introduction
The aim of this lab is to get familiar with Neural Networks. We will be using some code extracts that were implemented on the week 4 Classification I lab and build a Neural Network.
1.This lab is part of Assignment 1 part 2.
2.A report answering the **questions in red** should be submitted on QMplus along with the completed Notebook.
3.You should sibmit a single report a for both this AND the week 4 notebooks. 机器学习作业代做
4.The report should be a separate file inpd format(so NOT doc, docx, notebook etc.), well identified with your name, student number, assignment number (for instance, Assignment 1), module code.
5.Make sure that any figure or code a you comment on, are in cluded in the report.
6.No other means of submission other than the appropriate QM+ link is acceptable at any time (so NO email attachments, etc.)
7.PLAGIARISM is an irreversible non-negotiable failure in the course (if in doubt of what constitutes plagiarism, ask!).
For this lab, we will be using the iris dataset.
0.1 Intro to Neural Networks 机器学习作业代做
As covered in the lecture notes, Neural Networks (NN) are inspired by biological brains. Each “neuron” does a very simple calculation, however collectively they can do powerful computations.
A simple model neuron is called a Perceptron and is comprised of three components:
- The weights
- The input function
- The activation function
We can re-imagine the logistic regression unit as a neuron (function) that multiplies the input by the parameters (weights) and squashes the resulting sum through the sigmoid.
A Feed Forward NN will be a connected set of logistic regression units, arranged in layers. Each unit’s output is a non-linear function (e.g., sigmoid, step function) of a linear combination of its inputs.
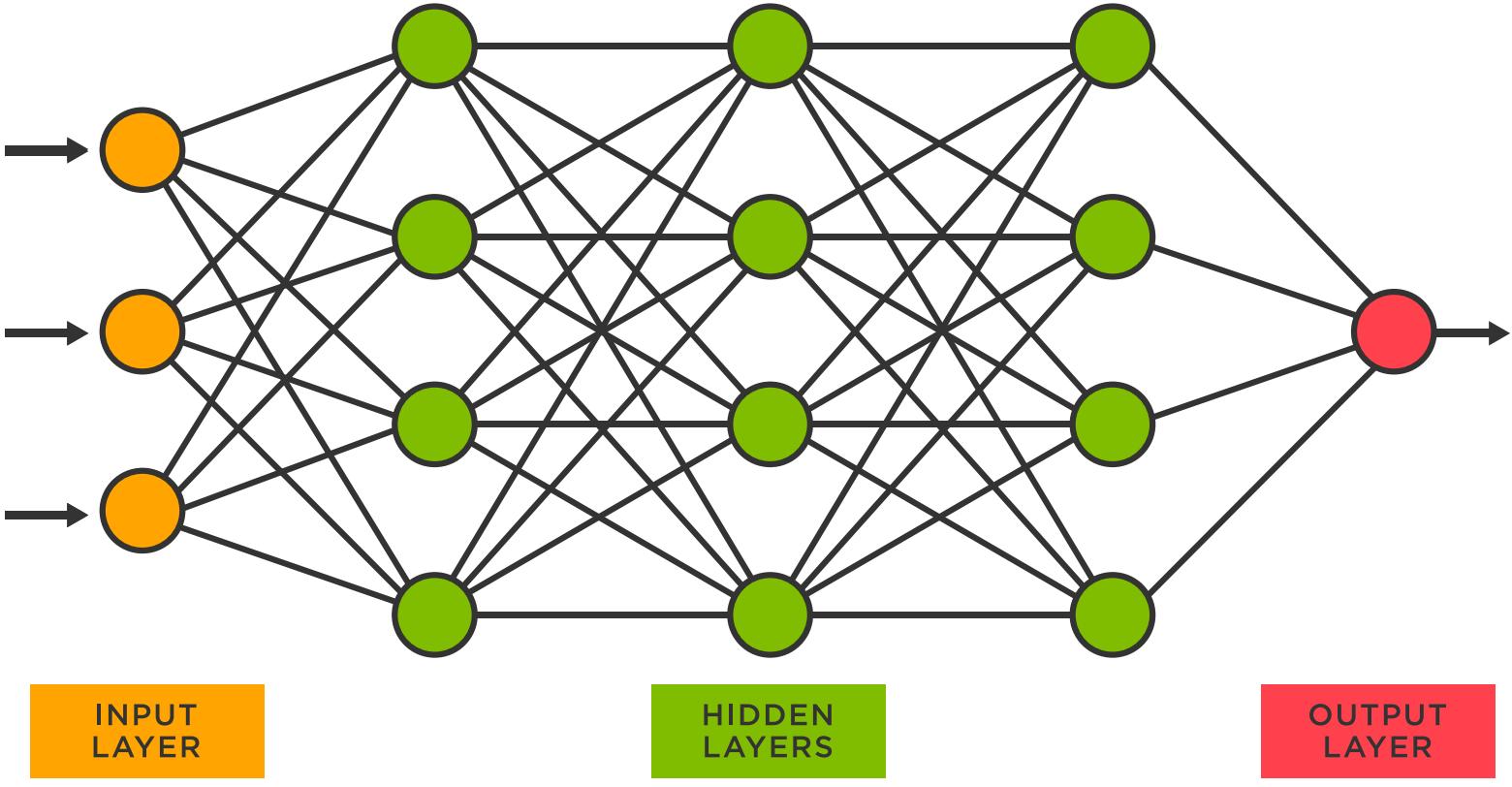
We will use the sigmoid as an activation function. Add the sigmoid function and LogisticRegression class from week 4 lab below. Change the parameter initialization in LogisticRegression , so that a random set offrom week 4 lab below. Change the parameter initialization in LogisticRegression , so that a random set of initial weights is used.
**Q1.** Why is it important to use a random set of initial weights rather than initializing all weights as zero in a Neural Network? [2 marks]
In [ ]:
In [ ]:
## sigmoid
In [ ]:
## logistic regression class
1. The XOR problem 机器学习作业代做
Let’s revisit the XOR problem.
In [ ]:
x1 = [0, 0, 1, 1]
x2 = [0, 1, 0, 1]
y = [0, 1, 1, 0]
c_map = [‘r’, ‘b’, ‘b’, ‘r’]
plt.scatter(x1, x2, c=c_map)
plt.xlabel(‘x1’)
plt.ylabel(‘x2’)
plt.show()
**Q2.** How does a NN solve the XOR problem? [1 marks]
We will implement back-propagation on a Feed Forward network to solve the XOR problem. The nework will have 2 inputs, 2 hidden neurons and one output neuron. The architecture is visualised as follows:
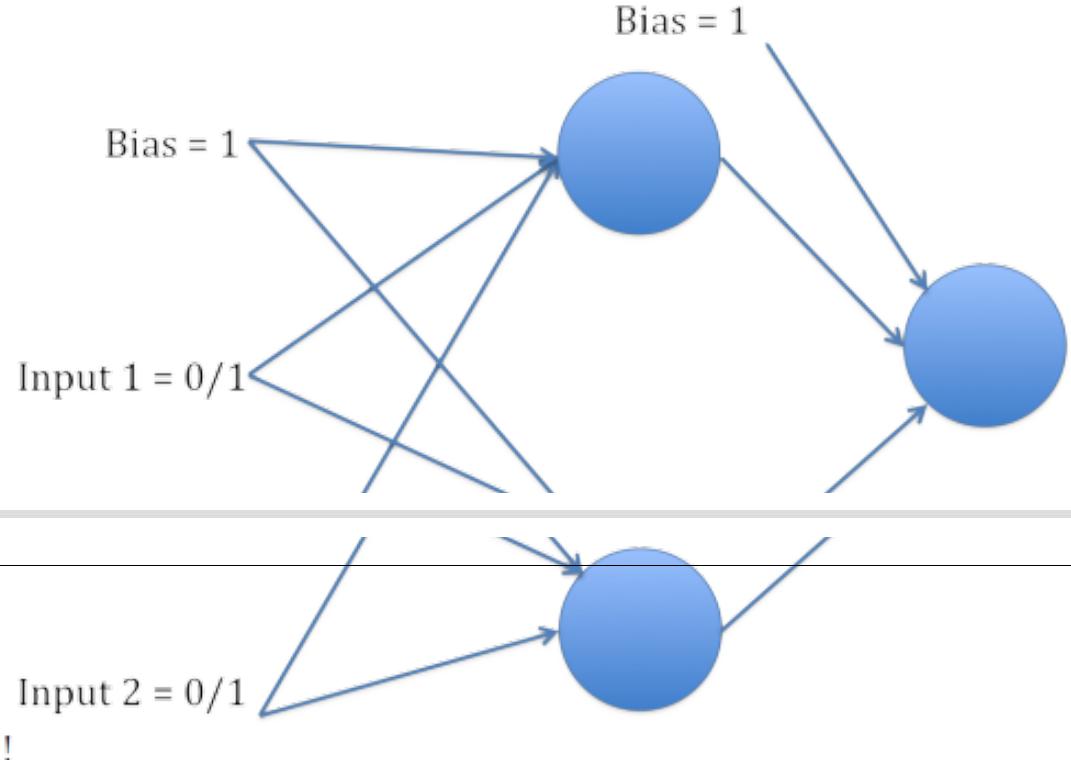
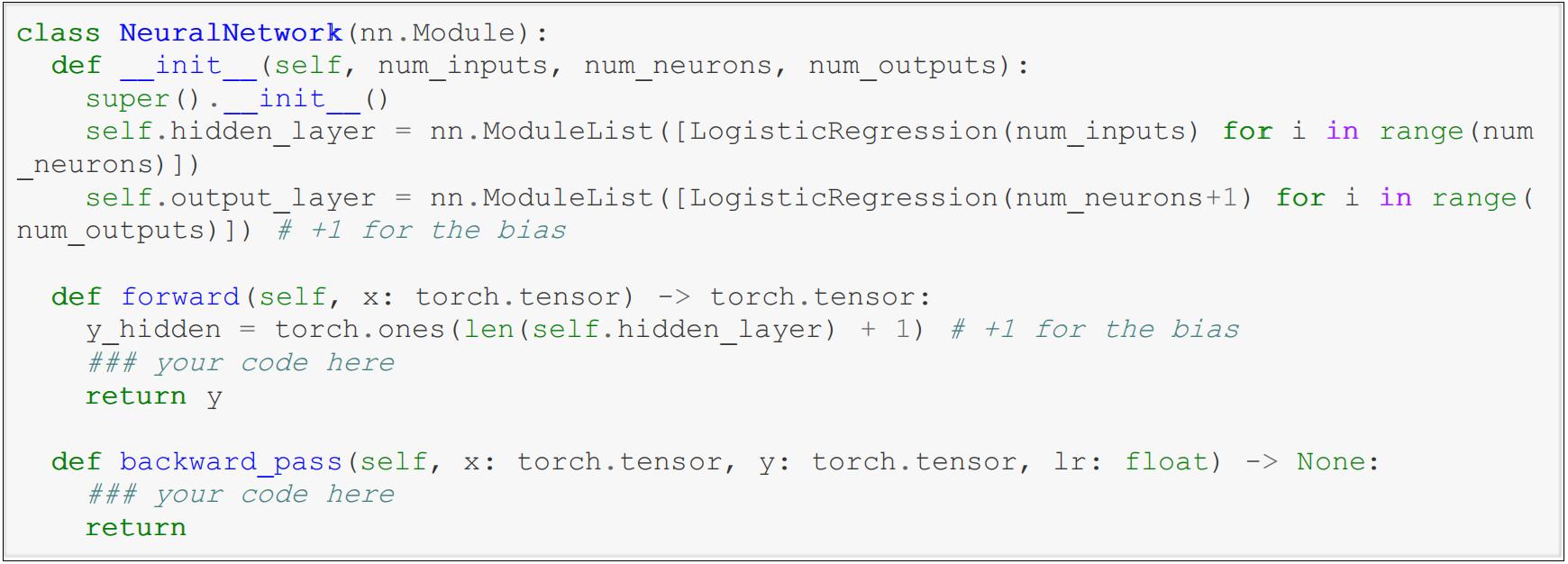
Using LogisticRegression and sigmoid from week 4 lab, implement the forward pass in the class below.
Assume a single sample at a time (i.e. the shape of x is (1, num_features )). [2 marks]
Hint: Check ModuleList documentation.
In [ ]:
In [ ]:
In the NeuralNetwork class above, fill in the backward_pass() method.
The implementation should support outputs of any size. To implement the backward pass, follow the steps below:
- Step 1:
For each output, k, calculate the partial derivative: 
\ where yk is the response of the output neuron and tk is the desired output (target). The derivative of the sigmoid function is defined as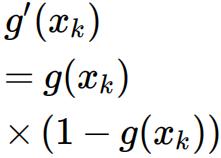 
[1 marks]
- Step 2:
We now need to probagate this error to the hidden neurons. To accomplish this remember that:
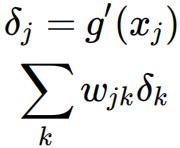
where is the error on the j-th hidden neuron, is the value of the hidden neuron (before it has been passed through the sigmoid function), is the derivative of the sigmoid function, is the error from the output neuron calculated in step 1, and is the weight from the hidden neuron to the output neuron . [1 marks]
-
Step3:
We now need to update the output weights, i.e. the connections from the hidden neurons to the output neurons. This is accomplished using the formula:
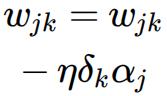
where wjk is the weight connecting the j-th hidden neuron to the k-th output neuron. aj is the activity of the j-th hidden neuron (after it has been transformed by the sigmoid function), δk is the error from the output neuron stored in output_deltas and η is the learning rate [1 mark]
- Step 4:
Finally we need to update the hidden weights, i.e. the connections from the hidden neurons to the inputs. Here, again we use this equation
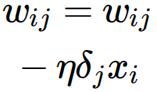
where is the weight connecting the i-th input to the j-th hidden neuron. is the i-th input, is the backpropagated error (i.e., hidden deltas) from the j-th hidden neuron and is the learning rate. [1 mark]
In [ ]:
# test it works
model.backward_pass(x_test, y_test, 1)
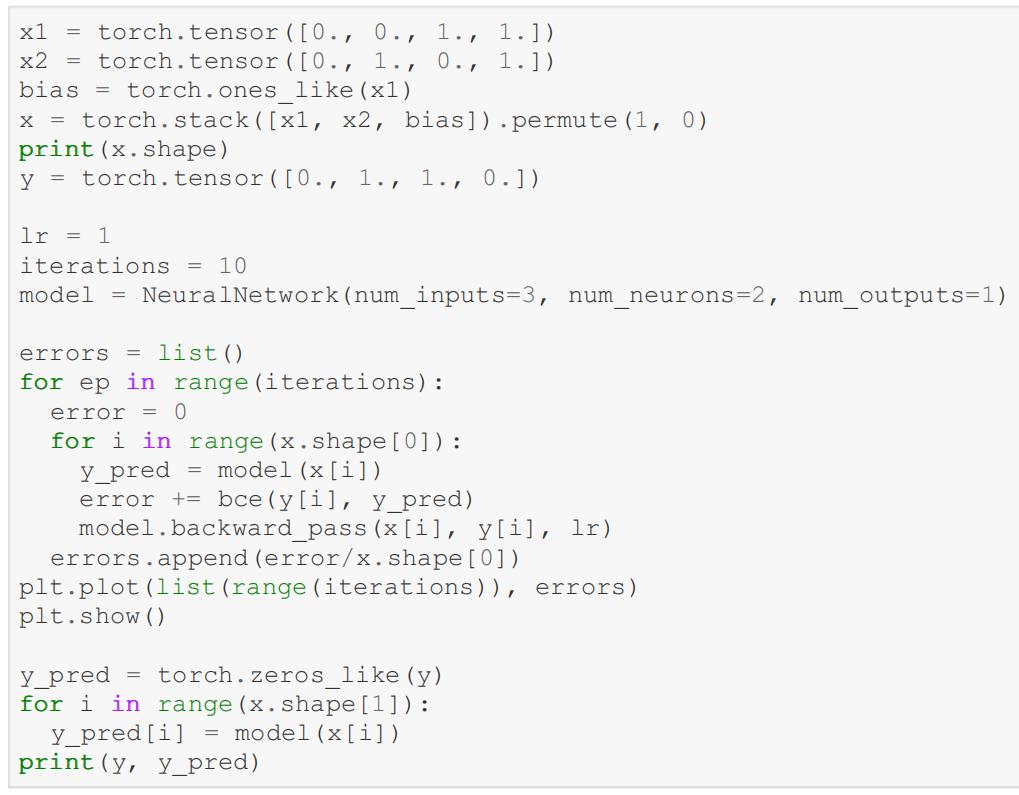
Now modify the code below to train a model on the XOR problem. Make sure to use an appropriate lr and number of iterations. Use the BCE method from week 4 to visualize cost. [1 mark]
In [ ]:
2. Iris Dataset 机器学习作业代做
We will now use pytorch built-in methods to create an MLP classifier for the iris dataset.
In [ ]:
iris = datasets.load_iris()
printp
(iris.DESCR)
Split the data to train and test sets (make sure the same random seed is used as previously) and normalize using the method from week 4. We will use all attributes in this lab. [2 marks]
In [ ]:
### your code here### your code here
Using pytorch built in methods (and using the training loop from week 4 as guideline for the train loop), build an MLP with one hidden layer. Train the network multiple times for the following number of hidden neurons {1, 2,4, 8, 16, 32} .
**Q3.** Explain the performance of the different networks on the training and test sets. How does it compare to the logistic regression example? Make sure that the data you are refering to is clearly presented and appropriately labeled in the report. [8 marks]
In [ ]:
your code here
更多代写：美国数学代考价格 雅思面授 网课代修代上多少钱 新加坡Essay代写 国际政治论文代写 英国Midterm代考价格
