MAT3375-Spring/Summer 2020
Sample mid-term II, Fall 2020
Introduction to time series analysis
Time: 2 hours
时间序列分析代考 If a formula was proved in lecture slides you do not need to prove it again. You can simply refer to page number in the lecture slides.
-
This exam is open book and should be completed at home indepen-dently.
- Thesolution to this exam should be submitted on line in In very You can either print the exam and complete it or prepare your solutions on separate papers referring your solutions to each of the questions clearly. Make sure to use a thick pen so that the scan or photos of your solution is legible. You are not allowed to consult with any other individuals during the time you write the exam. The final submitted mid-term should be in one single pdf file. 时间序列分析代考
- Any conduct constitute cheating, misrepresenting, or unfairness includ- ingunauthorized aids and assistance, personating another person and committing plagiarism will be reported and will be dealt with based on regulations on code of conduct in academic matters.
- Write your detailed responses in the space provided.
- At the end of exam you need to submit the test to brightspace.
- If you are registered with SASS, please email me your test. Add the additional time given to you based on the University of Ottawa’s rule and regulations.
- Where it is possible to check your work, do so.
- If you see any error in this exam, please report it on your paper.
- If a formula was proved in lecture slides you do not need to prove it again. You can simply refer to page number in the lecture slides.
GOOD LUCK!
1.Let yi.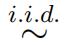 N (β , σ2), for i = 1, 2, . . . , m and yi.
N (β , σ2), for i = 1, 2, . . . , m and yi.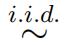 N (β1, σ2), for i =m + 1, m + 2, . . . , m + n. 时间序列分析代考
N (β1, σ2), for i =m + 1, m + 2, . . . , m + n. 时间序列分析代考
In other words the model
yi = β0 + si, i = 1, 2, . . . , m.
and
yi = β1 + si, i = m + 1, m + 2, . . . , m + n.
(i)Find M.L.E. for β0, β1and σ2.
(ii)Findthe distribution for βˆ0 and βˆ1.
(iii)Find an unbiased estimator for σ2
(iii) Explain how to test the null hypothesis
H0 : β0 = β1
against
H1 : β0 ƒ= β1.

2.The regression model 时间序列分析代考
yi = β0 + β1xi1 + β2xi2 + si, i = 1, 2, . . . , n = 19
with ∈ i.![]() N (0, σ2). From the ouput of R the matrix (X‘ X)−1 and some other information is given below:
N (0, σ2). From the ouput of R the matrix (X‘ X)−1 and some other information is given below:
> X=cbind(rep(1,length(x1)),x1, x2)
> length(x) [1] 20
> *X)
x1 x2
0.263228050 0.007856853 -0.04595048 时间序列分析代考
x1 0.007856853 1.713696862 -1.70212619
x2 -0.045950484 -1.702126187 1.69754457
>model=lm(y~x1+x2)
> anova(model)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F) 时间序列分析代考
x1 1 320.03 320.03 217.8253 9.74e-11 ***
x2 1 2.49 2.49 1.6949 0.2114
Residuals 16 23.51 1.47
> model$coef
(Intercept) x1 x2
1.570008 3.555795 -2.055999
>model2=lm(y~x1)
> anova(model2)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x1 1 320.03 320.03 209.27 5.494e-11 *** 时间序列分析代考
Residuals 17 26.00 1.53
—
Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
> model3=lm(y~x2)
> anova(model3)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x2 1 315.146 315.146 173.46 2.393e-10 ***
Residuals 17 30.886 1.817
—
Signif. codes: 0 *** 0.001 ** 0.01 * 0.05 . 0.1 1
> cor(x1,y) [1] 0.9617011
> cor(x2,y) [1] 0.9543288
> cor(x1,x2) [1] 0.9979624
(i)Find a 95% c.i. for β2. Make a decision based on your c.i. if we can acept
H0 : β2 = 0 at α = 5% level.
(ii)Check the validity of both model 2 and model 3. How do you explain your results based on the provided Routput?
(iii)Do you suggest removing x1as a predictor? Why?
3.Let 时间序列分析代考
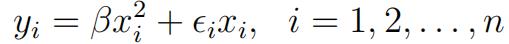
where ∈i.![]() N (0, σ2).
N (0, σ2).
(i)Explainhow we can write this model as a linear regression with the regular assumptions in this course. Does the regular assumptions hold?
(ii)Findthe L.E. for β and σ2 denoted by βˆ and σˆ2, respectively based on the modified model. Find the distribution for βˆ.

