时间序列分析代做 Time Series代写

Department of Computer & Mathematical Sciences

STAD57H3 Time Series Analysis

Duration: 180 minutes

Examination aids allowed: Open notes/books

时间序列分析代做 1. (Random Walk)Consider the random walk series Xt = Xt-1 + Wt, ∀t ≥ 1, where X0 = 0 and Wt ∼ WN(0, 1). Although the series is not stationary,

1. (Random Walk) 时间序列分析代做

Consider the random walk series X_t = X_t-1 + Wt, ∀_t ≥ 1, where X₀ = 0 and W_t ∼ WN(0, 1). Although the series is not stationary, assume we treat as such and calculate the sample auto-covariance function (based on a sample of size n) as

2. (Sum of AR(1) & MA(1) )

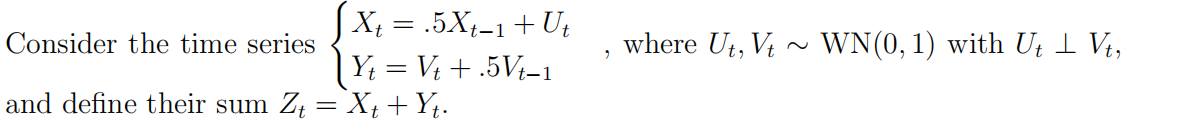
(a) [5 points] Find the auto-covariance function of Z_t.

(b) [7 points] Find the best linear predictor (BLP) of Z_n+1 based on X_n and Y_n only, and calculate its mean square prediction error (MSPE).

Answer all questions below in an .R/.RMarkdown fifile, and submit it on Quercus. Question data are in STAD57_W19_final.RData (use load() function).

4.(simulation) 时间序列分析代做

Simulate n = 100 observations of the zero-mean random walk (w/o drift) Xt from Question 1.

(a) [3 points] On the same graph, plot the sample auto-covariance of X_t for all possible lags, together with its expected value E[ˆγ(h)] from Q1 part (c).

Hint: Use acf(…, type = “covariance”, demean = F) for the sample autocovariance of a zero-mean process.

(b) [7 points] Perform the following bootstrap experiment: repeat the random walk simulation N = 1000 times, and save the sample auto-covariance function for each replicate. Plot the average sample auto-covariance function over all N bootstrap replicates, together with approximate 95% confifidence intervals and the theoretical expected value from Q1 part (c).

Hint: Use acf(…, plot = F) to speed up the calculation (avoid plotting).

5.(TS modeling) 时间序列分析代做

The time series tourists contains the monthly number of (non-resident) tourists entering Canada, from Jan 1972 to Dec 2018.

(a) [2 points] Plot the time series, its ACF and PACF, and comment on the series characteristics.

(b) [2 points] Plot the ACF and PACF of the difffferenced series at lag 12. Comment on whether the series seems seasonally integrated.

(c) [3 points] Fit a SARIMA(3, 0, 1)(0, 1, 2)[12] model to the series, and report the insample mean absolute prediction error.

(d) [3 points] Plot the diagnostics of your model from the previous part, and brieflfly comment.

(e) [3 points] Use the model to calculate and plot 1- to 36-step-ahead forecasts, and their associated 95% prediction intervals. Plot your forecasts and intervals at the end of the series.

6.(Forecasting) 时间序列分析代做

Consider the series Y, X, and Xnew (containing future values of X).

(a) [5 points] Examine Y graphically using appropriate plots, and comment of the following characteristics:

Trend (e.g. shape, deterministic/stochastic)
Seasonality (e.g. period, deterministic/stochastic)
Integrated (e.g. simple and/or seasonal)

(b) [5 points] Select a SARIMA model for X using AIC, and use it to make 1- to 35- step-ahead predictions. Report the out-of-sample mean absolute prediction error of your model, based on the values in Xnew.

(c) [8 points] (Extra Credit) Create a time series model for Y and use it to make 1- to 35-step-ahead predictions. You can use any type of model you like, and you can also take advantage of the information in X and Xnew. Your grade for this part will be based on the predictive performance of your model: your marks will be proportional to the relative accuracy of your forecasts (in terms of absolute error), compared to the accuracy of the best available model.

Save your predictions in a .txt fifile named with your student ID #, and submit it on Quercus. Use write( my_frcst, file = “<ID#>.txt” ) to save the vector of 35 forecasts; you can test if your fifile can be loaded properly with scan(“<ID#>.txt”). Page 9 of 12 (contd…)Extra Space (use if needed and clearly indicate which questions you are answering)

合作平台：随笔代写论文代写写手招聘英国留学生代写