Number Theory
数论作业代写 SHOW ALL WORK to get full marks. Leave answers as exact answers. For example, leave it as fractions such as 1\7 as opposed to decimals
Assignment 4 数论作业代写
SHOW ALL WORK to get full marks. Leave answers as exact answers. For example, leave it as fractions such as 1\7 as opposed to decimals such as 0.142857. Word problems should have sentence answers with units. Fractions should be in lowest terms.
As theory will be tested, quality of writing will be considering in marking. Only single display calculators are permitted. 数论作业代写
All assignments must be handed in via Crowdmark by 11:59pm on April 16th. Lateassignments will not be accepted. Failure to follow the instructions will result in a mark of 0. up to 5.6 in the textbook.
[7] 1.A number n is called deficient if the sum of all divisors n, not including n itself is less than n. In other words, σpnq <2n. 数论作业代写
(a)Determinethe smallest number which is neither deficient, nor perfect.
(b)Show that prime powers are always defificient.
(c)Let n be an integer and p be an odd prime less than 2n1 Show that 2np is not deficient.

[7] 2.The Liouville Lambda Function is the function
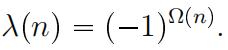
(a)Show λ is totally multiplicative, not just multiplicative. 数论作业代写
(b)Determine a formula for 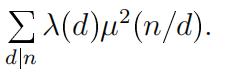
[7]3. Use the geometry method done in class and the videos to determine all solutions to x2 2y2 z2 where px, y, zq 1. 数论作业代写
[9] 4. Use the non-geometry method to determine all positive integer solutions to x2 +13y2 –z2 with px, y, zq 1.This assignment is out of 30 points.

更多代写:历史assignment代写 托福代考 留学生math作业代做 留学申请文书格式写作 留学生历史学论文代写 网课代管价格
