STATS 426
Winter, 2021
数理统计代考 Attempt all questions. Give short and speciftc answers. Show intermediate steps if there are any – to gain partial credits.
Exam #1 (Evening Exam-Schedule 2; due at 8pm)
Printed Name:—————————————————————
Signature:——————————————————————
UM unique name:—————————————————
- 1) Show your work and derivations, except for the questions in Problem #1 (Multiple Choices). A correct answer without derivations/procedures in other problems would get you NO Forthe sub-problems in Problem #1, you don’t need to give any explanation if you are sure your answer is correct. If you are not sure, a correct and relevant explanation could give you partial credits.
- 2)Make sure you upload your answer file to Canvas site before the given deadline; every additional minutes will cost you additional points until the score reaches 0.
- 3) Attempt all questions. Give short and speciftc answers. Show intermediate steps if there are any – to gain partial credits. 数理统计代考
- 4) Give only one answer to each question – if you give multiple potential answers, the worst answer will begraded.
• 5) During the exam time, you are not allowed to have interactions about the exam or course related materials with anyone other than the instructor. It would be considered cheating if you do so. Please complete the exam by yourself.
- 6) There are totally 10 questions in this exam. You have 60 minutes to complete the exam and a20-minute window to upload the pdf file.
GOOD LUCK

PROBLEM # 1:Multiple Choice — Choose the correct answer. Each multiple choice question is worth (4) points. 数理统计代考
1.1_____ If X1 and X2 both follow a Gamma distribution with parameter α > 0 and λ > 0 then
(A) P(X1 < 0) changes with the value of α (B) S = X1 + X2 is also a Gamma random variable
(C) P {(X1 + X2)/2 > 0} = .5 (D) none of the above is always true. 数理统计代考
1.2________The number of offspring of an organism is a discrete random variable with mean α and variance δ, where α > 0 and δ > Each of its offspring reproduces in the same manner. Suppose we have N1 = 5 organism at the first generation and N2, and N3 numbers of offspring at the second and third generation, respectively. Which of the following is correct.
(A) E(N2) = 5α. (B) V ar(N2) = 52δ.
(C) V ar(N3) = α2V ar(N2) + 52δα. (D) Two of the above (E) None of the above
1.3________Let X and Y be 2 random variables: E(X) = 0, var(X) = σ2> 0 and Y given X follows N (X, α), where α is a constant.
Let var(Y ) = σ2 . Then (A) α > 0 (B) σ2 = σ2+ α (C) X and Y are Y X Y positively correlated (D) None of the above is always true.
1.4________Let X be a continuous random variable with pdf, f , and a < b are real numbers. Is the 000following statement correct? “P (a ≤ X ≤ b) = f (a) + ∫ b f (s)ds + f (b).” 数理统计代考
(A) Yes (B) No
1.5________Let X, Y be joinly normally distributed with parameters µX , µY , σ2 , σ2 , and ρ. Let X Y fX|Y (x|y0) denote the conditional pdf of X given Y = y0. Let E(X|Y = y0) be the mean for fX|Y (x|y0).Also, σ2> 0 and σ2 > 0, then E(X|Y = y0)
(A) ≥ µX if y0 > µY and ρ > 0 (B) ≤ µX if y0 < µY and ρ < 0
(C) ≤ µY if y0 > µY and ρ < 0 (D) ≥ µY if y0 < µY and ρ > 0
PROBLEM # 2: 数理统计代考
Consider tossing a coin, with outcomes, H & T, and P(H) = π0. Each time, if you get a head, you pick up 3 blue balls and if you get a tail, you pick up 1 red ball.
2.1(5 pt) Suppose you toss a coin independently 2 times and let Y = the toal number of balls (no matter it is red or blue). Please provide the pmf function for Y and show it is a pmf function.
2.2(5 pt) Suppose you toss a coin independently n times and let Y = the toal number of balls. What isthe distribution of Y when n → ∞? Please show how you obtain your answer and report the distribution and its parameters.
PROBLEM # 3: 数理统计代考
Let X1 and X2 be two independent random variables with pdf, fX (x), and fX (x) =θ2e−θ2x, when x ≥ 0; f (x) = 0, otherwise. Also let V = X − X .
3.1(5 pt) What would be the pdf of (V )? Justify that your answer is a pdf.
3.2(5pt) Suppose we generate 3 random numbers from Uniform distribution, U[0,1], and they are 0.1, 0.24and 0.36. Using these 3 numbers, how should we obtain 3 random numbers generated from the distribution of V ?
PROBLEM # 4:
Suppose Yn ∼ Poisson(θn) where θn → ∞, witn n → ∞. Please use the moment generating functions of Yn to show that when n → ∞,
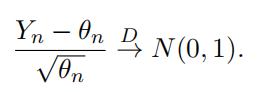
That is Yn converge in distribution to a normal distribution. The Poisson mgf is exp{θ(exp(t) − 1)}.

更多代写:代做c/c++语言作业 代做quiz 电子工程essay代写 电影学essay代写 出国论文代写作 财务管理论文代写
