数据结构之AVL树

1. 简述

AVL树是最开始明确提出的自平衡二叉树，在AVL树中一切连接点的2个子树的高宽比较大 区别为一，因此它也被称作高宽比平衡树。AVL树而出名于它的发明人G.M. Adelson-Velsky和E.M. Landis。AVL树种搜索、插进和删掉在均值和最坏状况下全是O（log n），提升和删掉很有可能必须根据一次或数次树转动来再次均衡这一树。文中详细介绍了AVL树的设计方案观念和操作过程。

2. 基础专业术语

有四诸多状况很有可能造成二叉查找树不平衡，各自为：

（1）LL：插进一个新连接点到根节点的左子树（Left）的左子树（Left），造成根节点的均衡因素由1变成2

（2）RR：插进一个新连接点到根节点的右子树（Right）的右子树（Right），造成根节点的均衡因素由-1变成-2

（3）LR：插进一个新连接点到根节点的左子树（Left）的右子树（Right），造成根节点的均衡因素由1变成2

（4）RL：插进一个新连接点到根节点的右子树（Right）的左子树（Left），造成根节点的均衡因素由-1变成-2

对于四诸多状况很有可能造成的不平衡，能够根据转动使之变均衡。有二种基础的转动：

（1）左转动：将根节点转动到（根节点的）右小孩的左小孩部位

（2）右转动：将根节点转动到（根节点的）左小孩的右小孩部位

3. AVL树的转动实际操作

AVL树的操作过程是转动，有四种转动方法，各自为：左转动，右转动，上下转动（先左后右），右左转动（先后右左），事实上，这四种转动实际操作两组对称性，因此还可以称作两大类转动实际操作。

基础的算法设计：

typedef  struct  Node* Tree;
typedef  struct  Node* Node_t;
typedef  Type int;
struct  Node{
 Node_t left;
 Node_t right;
 int  height;
 Type data;
};
int  Height(Node_t node) {
 return  node->height;
}

3.1 LL

LL状况必须左旋体处理，如下图所显示：

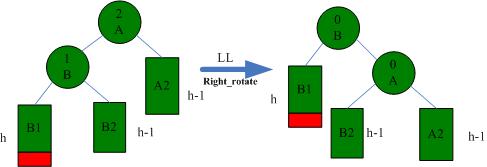
编码为：

Node_t RightRotate(Node_t a) {
 b = a->left;
 a->left = b->right;
 b->right = a;
 a->height = Max(Height(a->left), Height(a->right));
 b->height = Max(Height(b->left), Height(b->right));
 return  b;
}

3.2 RR

RR状况必须左旋体处理，如下图所显示：

编码为：

Node_t LeftRotate(Node_t a) {
 b = a->right;
 a->right = b->left;
 b->left = a;
 a->height = Max(Height(a->left), Height(a->right));
 b->height = Max(Height(b->left), Height(b->right));
 return  b;
}

3.3 LR

LR状况必须上下（先B左转动，后A右转动）旋处理，如下图所显示：

编码为：

Node_t LeftRightRotate(Node_t a) {
 a->left = LeftRotate(a->left);
 return  RightRotate(a);
}

3.4 RL

RL状况必须右左旋体处理（先B右转动，后A左转动），如下图所显示：

编码为：

Node_t RightLeftRotate(Node_t a) {
 a->right = RightRotate(a->right);
 return  LeftRotate(a);
}

4. AVL数的插进和删掉实际操作

(1) 插进实际操作：事实上便是在不一样状况下选用不一样的转动方法调节整棵树，实际编码以下：

Node_t Insert(Type x, Tree t) {
 if(t == NULL) {
   t = NewNode(x);
 } else  if(x < t->data) {
   t->left = Insert(t->left);
   if(Height(t->left) - Height(t->right) == 2) {
    if(x < t->left->data) {
     t = RightRotate(t);
    } else  {
     t = LeftRightRotate(t);
    }
  }
 } else  {
   t->right = Insert(t->right);
   if(Height(t->right) - Height(t->left) == 2) {
    if(x > t->right->data) {
     t = LeftRotate(t);
    } else  {
     t = RightLeftRotate(t);
    }
  }
 }
 t->height = Max(Height(t->left), Height(t->right))   1;
 return  t;
}

(2) 删掉实际操作：最先精准定位要删掉的连接点，随后用该连接点的右小孩的最左小孩更换该连接点，并再次调节以该连接点为根的子树为AVL树，实际调节方式跟插进数据信息相近，编码以下：

Node_t Delete(Type x, Tree t) {
 if(t == NULL) return  NULL;
 if(t->data == x) {
  if(t->right == NULL) {
   Node_t temp = t;
   t = t->left;
   free(temp);
  } else  {
   Node_t head = t->right;
   while(head->left) {
    head = head->left;
   }
   t->data = head->data; //just copy data
   t->right = Delete(t->data, t->right);
   t->height = Max(Height(t->left), Height(t->right))   1;
  }
  return  t;
 } else  if(t->data < x) {
  Delete(x, t->right);
  if(t->right) Rotate(x, t->right);
 } else  {
  Delete(x, t->left);
  if(t->left) Rotate(x, t->left);
 }
 if(t) Rotate(x, t);
}

5. 小结

AVL树是最开始的自平衡二叉树，对比于之后出現的平衡二叉树（红黑树，treap，splay树）来讲，它如今运用较少，但科学研究AVL树针对掌握后边出現的常见平衡二叉树具备关键实际意义。

6. 参考文献

（1） 算法设计（C语言版） 严蔚敏，吴黄伟著

（2） http://zh.wikipedia.org/wiki/AVL树

（3）http://www.cppblog.com/goodwin/archive/2011/08/08/152797.html

（4）http://www.asiteof.me/2010/06/avl/